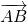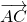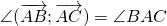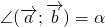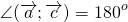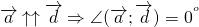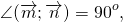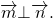Что называется углом между двумя векторами
Угол между векторами.
 |
Формула вычисления угла между векторами
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Как найти угол между векторами
Угол между векторами
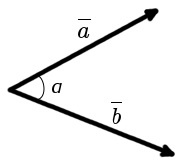
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
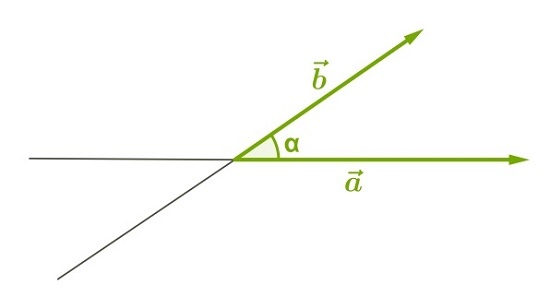
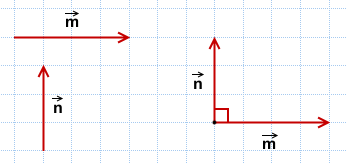
Острый:
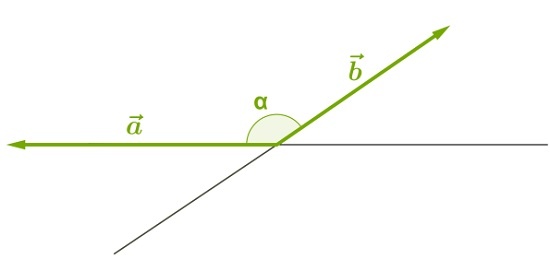
Тупой:
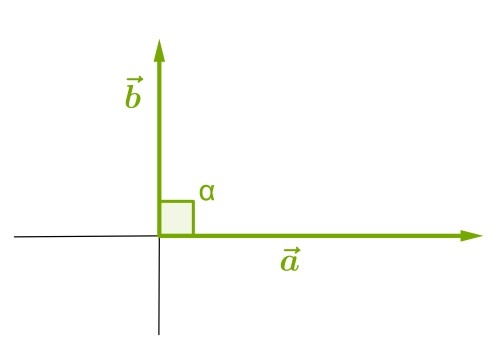
Прямой:
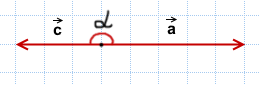
С величиной \(0^\circ\) (то есть, векторы сонаправлены):
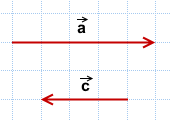
С величиной \(180^\circ\) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между \( \overrightarrow a\) и \(\overrightarrow b\) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
\(\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat<\overrightarrow a;\overrightarrow b>\right)\)
В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
Расчет угла, если вектор задан координатами
Если же координаты находятся в трехмерном пространстве и заданы в виде:
то формула принимает такой вид:
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Решение
Для начала найдем их координаты по известным координатам заданных точек:
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Решение
Подставим известные значения:
Далее найдем угол между данными векторами:
Задача 2
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
Подставляем значения и получаем:
Теперь находим угол α:
Задача 3
Вектор. Скалярное произведение векторов. Угол между векторами.
Скалярным произведением (или внутренним произведением) 2 векторов есть операция с двумя
векторами, итогом чего является число (скаляр), которое не зависит от системы координат и которое
характеризует длины векторов-сомножителей и угол между векторами.
Также скалярным произведением двух векторов называется число, которое
равно произведению модулей 2 векторов на косинус угла между векторами.
Скалярное произведение векторов формула:

Этой операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта
операция зачастую рассматривается как коммутативная и линейная по каждому из сомножителей.
Скалярное произведение векторов 



значения, т.е. 
Еще используются такие обозначения: 


В основном имеется ввиду, что скалярное произведение определено положительно, т.е.
при каждом 
(неопределенным).
Если хотя бы один из 2 векторов 


Свойства скалярного произведения векторов.
1. 
2. 

3. Если 
4. Если и 



5.
6.
7.
Если же векторы 



произведение векторов, формула:
Формула для определения длины вектора:
Длина (модуль) вектора, с известными координатами, равен квадратному корню из суммы квадратов
Длина вектора 
Как определить угол между 2 векторами:
Как найти угол между двумя векторами 

Ежели угол меж двумя векторами острый, то их скалярное произведение имеет положительный знак; если
же угол между двумя векторами тупой, то их скалярное произведение имеет отрицательный знак.
Скалярное произведение двух ненулевых векторов равно нулю, тогда и только тогда, когда эти векторы
ортогональны.
Альтернативное определение скалярного произведения векторов (вычисление скалярного
произведения двух векторов, заданных своими координатами).
Вычислить координаты вектора, если заданы координаты его начала и его конца очень просто. Давайте
рассмотрим этот вопрос:
Исходя из этого, координаты вектора АВ:
Точно так же и в двухмерном пространстве – разница в отсутствии третьих координат.
Итак, предположим, даны два вектора, которые заданы набором координат своих точек:
а) В двухмерном пространстве (плоскость):
Значит, скалярное произведение этих векторов вычислим по формуле:
б) В трехмерном пространстве:
Как и в двухмерном случае, скалярное произведение двух векторов вычисляем по формуле:
Угол между векторами
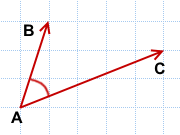
1) Углом между векторами
называется угол BAC:
2) Углом между двумя ненулевыми векторами называется угол между векторами, равными данным и имеющими общее начало.
Поскольку нулевой вектор считается коллинеарным любому вектору, если один из векторов нулевой либо если оба вектора нулевые, то и в этом случае угол между векторами равен 0°.
Угол между равными векторами также равен 0°.
Угол между противоположно направленными векторами равен 180°.
Если угол между векторами равен 90°, то такие векторы называются перпендикулярными.
Рассмотрим понятие угла между векторами на конкретных примерах.
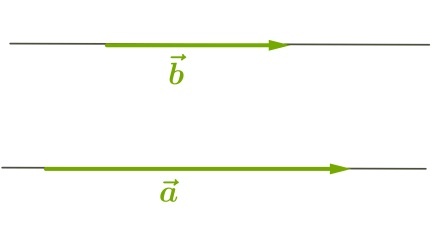
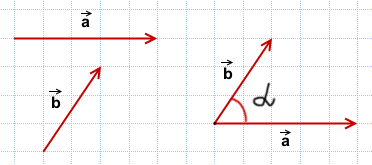
Определить угол между векторами:
1) Данные векторы не сонаправлены.
Выберем некоторую точку и от неё отложим векторы, равные данным.
Угол между ними равен α.
Значит, и угол между данными векторами равен α.
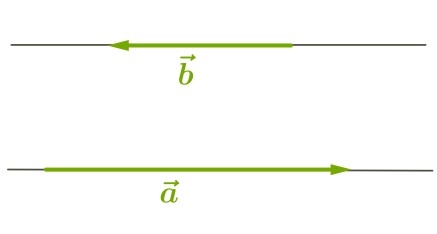
2) Данные векторы противоположно направлены.
Значит, угол между ними равен 180°:
Проиллюстрируем этот результат, отложив векторы, равные данным, от одной точки:
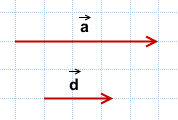
4) Отложим данные векторы от общего начала.
Так как угол между ними равен 90°:
Угол между векторами можно найти с помощью их скалярного произведения.
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Решение
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Решение
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Решение
и отсюда выведем формулу косинуса угла:
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу: