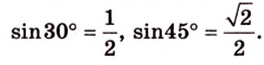Что называется углом между двумя прямыми в пространстве
Угол между прямыми в пространстве
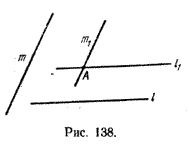
Пусть в пространстве заданы прямые l и m. Через некоторую точку А пространства проведем прямые l1 || l и m1 || m (рис. 138).
Заметим, что точка А может быть выбрана произвольно, в частности она может лежать на одной из данных прямых. Если прямые l и m пересекаются, то за А можно взять точку пересечения этих прямых (l1 = l и m1 = m).
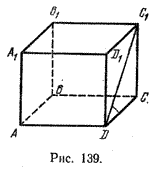
Найти угол между прямыми АВ и DС1.
Прямые АВ и DС1 скрещивающиеся. Так как прямая DC параллельна прямой АВ, то угол между прямыми АВ и DС1, согласно определению, равен \(\widehat
Следовательно, \(\widehat<(AB;DC_1)>\) = 45°.
Прямые l и m называются перпендикулярными, если \( \widehat <(l;m)>\) = π /2. Например, в кубе
Вычисление угла между прямыми.
Пусть прямые заданы своими каноническими уравнениями
Тогда угол φ между прямыми определяется с помощью формулы
Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).
Задача 1. Вычислить угол между прямыми
Направляющие векторы прямых имеют координаты:
По формуле (1) находим
Следовательно, угол между данными прямыми равен 60°.
Задача 2. Вычислить угол между прямыми
Аналогично находим направляющий вектор второй прямой:
Но формуле (1) вычисляем косинус искомого угла:
Следовательно, угол между данными прямыми равен 90°.
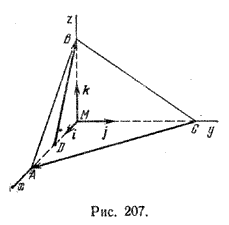
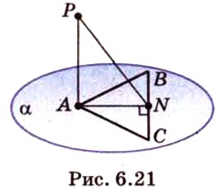
Задача 3. В треугольной пирамиде МАВС ребра MA, MB и МС взаимно перпендикулярны, (рис. 207);
По таблице косинусов находим, что угол между прямыми СА и DB равен приблизительно 72°.
Угол между скрещивающимися прямыми : определение, примеры нахождения
В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
Рассмотрим рисунок, приведенный ниже.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.
Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Для нахождения искомого угла между a 1 и b 1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a 1 и b 1 .
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
A D → и B C → являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
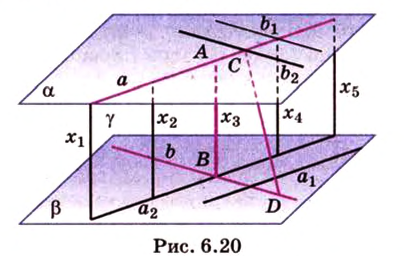
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
Угол между пересекающимися прямыми: определение, примеры нахождения
Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.
Что такое угол между пересекающимися прямыми
Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.
Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.
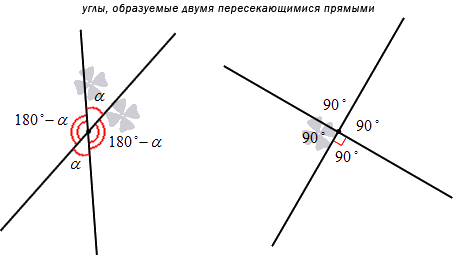
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.
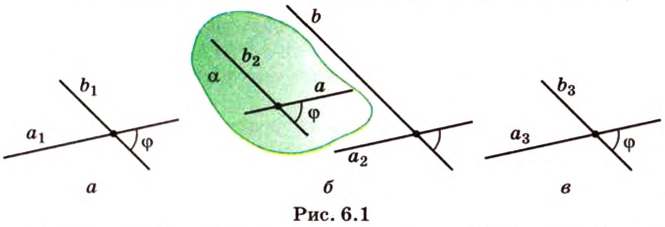
Взгляните на рисунок:
Перейдем к формулированию основного определения.
Как найти угол между пересекающимися прямыми на плоскости
Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.
Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.
Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.
Начнем с формулировки основного принципа нахождения угла в заданных условиях.
Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.
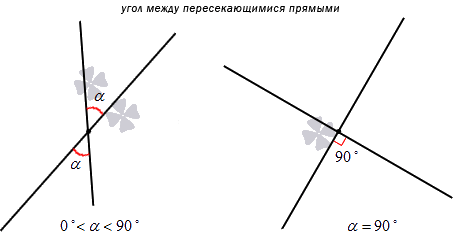
Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:
Теперь рассмотрим каждый способ отдельно.
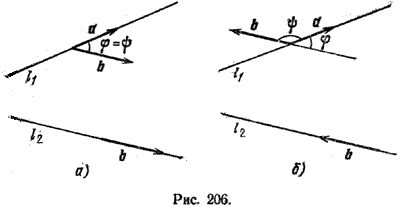
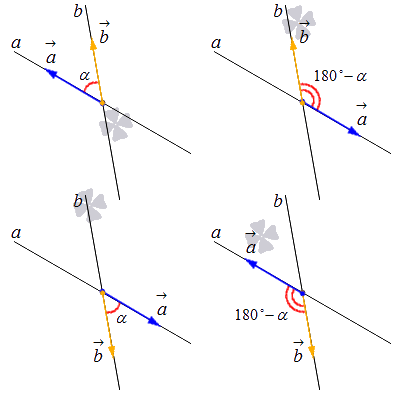
Во втором случае были использованы формулы приведения. Таким образом,
Запишем последнюю формулу словами:
Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.
Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:
cos α = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2 = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
Тогда сам угол можно найти по следующей формуле:
α = a r c cos a x · b x + a y + b y a x 2 + a y 2 · b x 2 + b y 2
Приведем пример решения задачи.
Решение
Ответ: данные прямые образуют угол в 45 градусов.
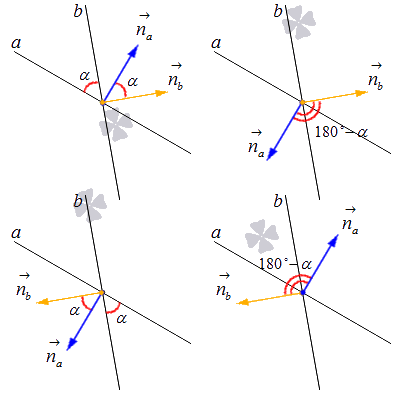
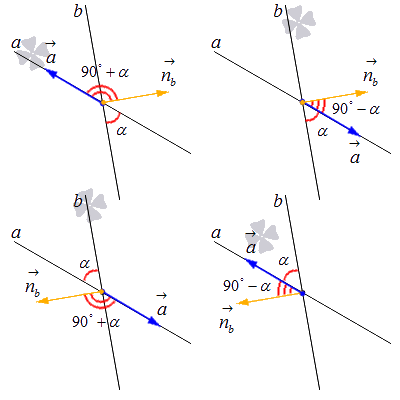
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:
Здесь n a → и n b → обозначают нормальные векторы двух заданных прямых.
Решение
Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.
Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.
Если он менее 90 градусов, то мы получим следующее:
Используя правило равенства косинусов равных углов, запишем:
Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.
Запишем необходимые формулы. Нахождение синуса угла:
Нахождение самого угла:
α = a r c sin = a x · n b x + a y · n b y a x 2 + a y 2 · n b x 2 + n b y 2
Здесь a → является направляющим вектором первой прямой, а n b → – нормальным вектором второй.
Решение
Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.
Ответ: α = a r c sin 7 2 34
Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.
Решение
Ответ: α = a r c cos 23 2 34
В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.
Как вычислить угол между пересекающимися прямыми в пространстве
Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.
Для нахождения самого угла нам понадобится эта формула:
α = a r c cos a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Решение
Содержание:
Угол между двумя прямыми в пространстве
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 
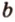
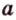
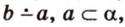
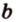
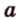
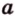
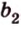
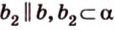
Итак,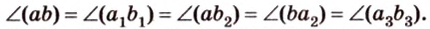
Если 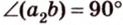
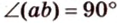
Угол между прямой и плоскостью в пространстве
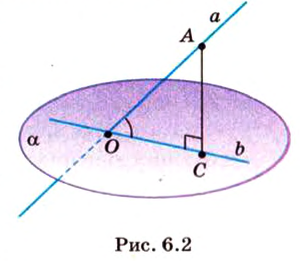
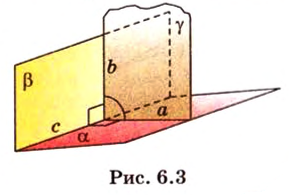
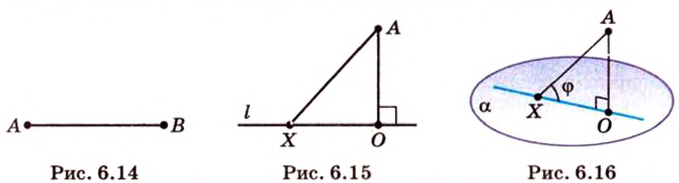
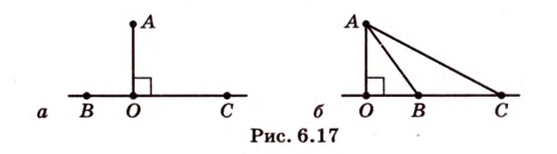
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 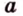
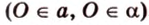
Угол между двумя плоскостями, пространства
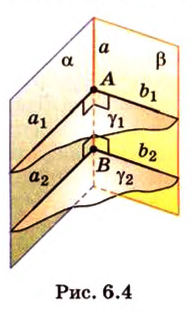
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например 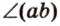
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Пример №1
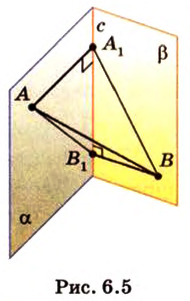
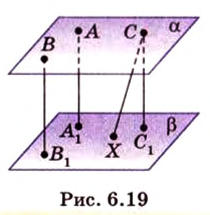
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 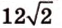
Дано: 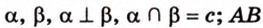
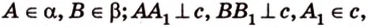
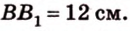
Найти: углы, образованные отрезком 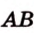
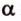
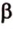
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
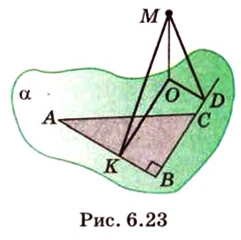
Расстояния в пространстве
Рассмотрим плоскость 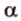
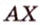
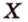
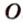
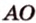
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
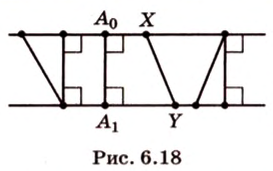
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 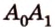
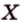
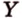
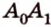
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Пусть имеем две параллельные плоскости 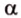
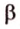
и второй, то перпендикуляр 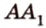
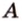
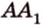
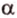
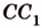
А это вытекает из того, что перпендикуляр 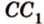
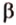
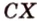
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Действительно, пусть 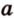
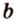
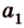
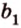
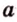
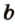
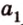
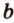
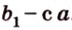
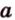
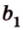
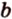
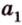
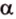
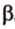
Плоскости 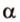
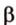
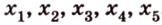
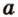
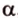
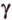
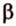
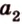
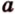
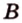
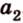
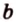
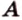
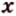
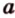
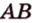
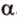
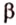
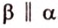
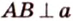
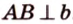
Отрезок 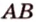
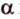
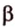
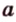
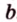
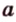
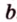
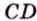
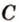
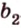
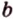

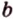
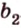
Поскольку она перпендикулярна прямым 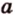
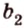

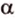




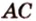
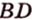
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Пример №2
Отрезок 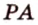
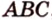
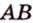
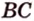
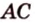
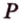
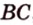
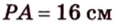
Пусть 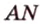
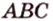
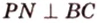
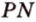
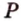
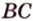
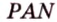
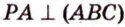
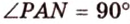
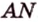
Из формулы для площади треугольника 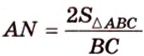
Необходимую площадь определим по формуле Герона: 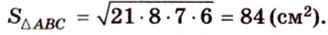
Тогда 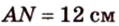
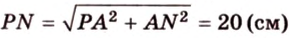
Пример №3
Прямая 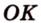
Пусть 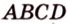
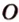
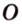
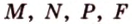
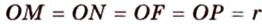
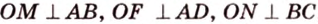
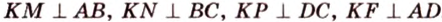
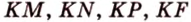
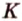
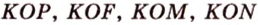
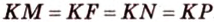
Пример №4
Точка 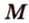
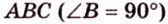
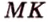
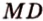
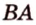
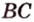
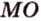
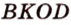
Поскольку отрезки 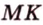
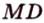
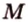
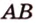
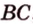
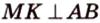
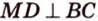
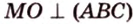
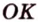
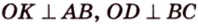
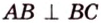
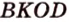
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.