Что называется удельным зарядом частицы

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЧАСТИЦЫ МЕТОДОМ ОТКЛОНЕНИЯ В МАГНИТНОМ ПОЛЕ

Ознакомьтесь с теорией в конспекте и учебниках: 1. Трофимова Т.И. Курс физики. Гл. 14, §115. 2. Детлаф А.А., Яворский Б.М. Курс физики. Гл. 23, §23.3.Запустите программу «Электричество и магнетизм». Выберите: «Масс-спектрометр». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).

· Знакомство с компьютерным моделированием движения заряженных частиц в магнитном поле.

· Ознакомление с принципом работы масс-спектрометра.

· Определение удельного заряда частиц.

1. СИЛА ЛОРЕНЦА- сила, действующая на движущуюся со скоростью v в однородном магнитном поле с индукцией В частицу с зарядом q:

(1)

Модуль этой силы равен

, (2)

где a- угол между векторами и . Сила Лоренца направлена перпендикулярно скорости частицы, сообщает ей только нормальное ускорение и вызывает искривление траектории частицы.

Если частица влетает в однородное магнитное поле в направлении, перпендикулярном линиям магнитной индукции, то частица будет двигаться по дуге окружности, плоскость которой перпендикулярна линиям индукции. Радиус окружности можно найти из второго закона динамики:

. (3)

УДЕЛЬНЫМ ЗАРЯДОМ ЧАСТИЦЫ называется отношение заряда частицы к её массе. Тогда из формулы (3) удельный заряд будет равен:

. (4)

Период обращения частицы равен

, (5)

и не зависит от скорости.

МАСС-СПЕКТРОМЕТРОМ называется прибор, для разделения ионизованных молекул и атомов (изотопов) по их массам, основанный на воздействии электрических и магнитных полей на пучки ионов, летящих в вакууме.

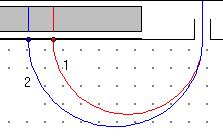
Простейшая модель масс-спектрографа показана на рис. 1.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

1.Подведите маркер мыши к движку регулятора величины магнитной индукции, нажмите левую кнопку мыши и, удерживая ее в нажатом состоянии, двигайте движок, установив числовое значение В, взятое из таблицы 1 для вашей бригады.

2. Аналогичным образом, зацепив мышью движок регулятора скорости, установите минимальное значение 10 3 м/с.

4. Нажмите мышью кнопку «Старт» и синхронно секундомер. Проследите за движением двух изотопов в магнитном поле модельного масс-спектрометра и по секундомеру определите время этого движения.

5. Запишите в таблицу 2 значения радиусов окружностей, по которым двигались эти изотопы (они показаны красным и синим цветом в правом углу окна) и время движения изотопов в вакуумной камере масс-спектрометра.

6. Последовательно увеличивая скорость частиц на 10 3 м/с, проделайте п.п.4-5 ещё 9 раз и заполните таблицу 2.

8. Проведите аналогичные измерения с изотопами урана и неизвестного химического элемента и заполните таблицы 4 и 5.

Таблица 1. Значения магнитной индукции В

Таблицы 2-5. Результаты измерений и расчётов

ОБРАБОТК РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:

1. Вычислите по формуле (4) удельные заряды изотопов углерода, неона, урана и неизвестного химического элемента и запишите полученные значения в соответствующие таблицы.

2. Используя справочные материалы по физике и химии, определите табличные значения удельных зарядов исследованных изотопов и сравните их с полученными в опыте.

3. Постройте график зависимости времени пролёта изотопов в камере масс-спектрометра от их скорости и сделайте выводы по результатам анализа этого графика.

4. Проведите оценку погрешностей проведённых измерений.

Вопросы и задания для самоконтроля

1. Как определяется направление действия силы Лоренца?

2. Почему сила Лоренца не совершает работы?

3. Как будет двигаться заряженная частица в магнитном поле, если угол a между векторами и меньше p/2?

5. Определите, во сколько раз изменится радиус окружности, по которой заряженная частица движется в однородном магнитном поле, если её кинетическую энергию увеличить в n раз?

6. Определите удельный заряд иона, который в масс-спектрометре совершает один оборот за 628 мкс в однородном магнитном поле с индукцией 50 мТл.

7. Пучок ионов, влетающих в вакуумную камеру масс-спектрометра перпендикулярно силовым линиям однородного магнитного поля, расщепляется (рис.2). Определите, какая траектория соответствует: а) большему импульсу,

если ионы имеют одинаковые заряды, но разные импульсы; б) большему заряду, если частицы имеют одинаковые импульсы, но разные заряды?

8. Два электрона движутся в одном и том же однородном магнитном поле по орбитам с радиусами R₁ R₂ (R₁> R₂). Сравните их угловые скорости.

9. В однородном магнитном поле движутся по окружностям протон и a-частица, имея равные кинетические энергии. Какая из этих частиц будет иметь орбитальный магнитный момент и период вращения больше и во сколько раз?

10. Заряженная частица влетела в однородное магнитное поле под углом a

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Определение удельного заряда электрона ответы

Oct 7, 2019 · 5 min read

Цель работы: определить удельный заряд электрона с помощью магнетрона.

Траектория и другие характеристики движения заряженной частицы в электрическом и магнитном полях определяются конфигурацией этих полей, ориентацией вектора скорости и отношением заряда частицы к ее массе (удельным зарядом). На заряженную частицу, движущуюся в магнитном поле, действует сила, которую называют магнитной:

СКАЧАТЬ ЯНДЕКС ДИСКА ОТВЕТЫ

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

где q — заряд частицы; v — её скорость; B — и н дукция магнитного поля. Направлена эта сила перпендикулярно плоскости, в которой лежат векторы v и B. Модуль магнитной силы F = qvB sin a, где a — угол между векторами v и B. Если имеются одновременно электрическое и магнитное поля, то сила, действующая на заряженную частицу, называется силой Лоренца и определяется как F = q(E+v×B), где Е — напряженность электрического поля.

Существуют различные методы определения удельного заряда электрона е/т (e — абсолютная величина заряда электрона, m — его масса), в основе которых лежат законы движения электрона в электрическом и магнитном полях. Один из них — метод магнетрона (конфигурация полей в нем напоминает конфигурацию полей в магнетронах — генераторах электромагнитных колебаний сверхвысоких частот). Метод магнетрона состоит в следующем. Электронная лампа с двумя цилиндрическими коаксиальными электродами помещается

СКАЧАТЬ ЯНДЕКС ДИСКА ОТВЕТЫ

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

внутри соленоида с той же осью. При разности потенциалов между электродами возникает электрическое поле. При пропускании тока в соленоиде создается магнитное поле. Электроны эмитируются нагретым катодом (внутренним электродом). Если тока в соленоиде нет, электроны движутся радиально к аноду (внешнему электроду). Устанавливается анодный ток. При токе в соленоиде на электроны начинает действовать магнитная сила, под действием которой их траектории искривляются. При увеличении тока в соленоиде электроны перестают достигать анода. Анодный ток падает. Рассмотрим подробнее движение электрона во взаимно перпендикулярных электрическом и магнитном полях. Электрическое поле направлено радиально к оси магнетрона, магнитное поле — вдоль этой оси. Введем цилиндрическую систему координат, в которой положение электрона определяется расстоянием r от оси, полярным углом j в плоскости, перпендикулярной оси, и координатой z вдоль оси. Движение электрона в двухэлектродной лампе в магнитном поле соленоида показано на рис. 1.

СКАЧАТЬ ЯНДЕКС ДИСКА ОТВЕТЫ

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Кинетическая энергия электрона будет равна работе сил электрического поля

где U — потенциал относительно катода точки поля, в которой находится электрон. Подставляя в (3) значение vj из (2), получаем

Вблизи анода r = ra (rа — радиус анода) и U = Ua (Ua — анодное напряжение). Для каждого значения анодного напряжения Uа при некотором значении магнитной индукции B = Вкр, которое называют критическим, скорость электрона вблизи анода станет перпендикулярной радиусу (vr = 0). Тогда уравнение (4) примет вид

Таким образом, если задано Ua и известно Вкр, можно определить е/m. Индукция B пропорциональна току в соленоиде Iс. На рис. 2 показана экспериментальная зависимость анодного тока Iа от тока в соленоиде Iс (сбросовая характеристика).

Если бы у всех электронов параметры движения были бы одни и те же, зависимость анодного тока от тока в соленоиде имела бы вид, показанный пунктирной линией. В этом случае при Iс Iкр ни один электрон не попадал бы на анод. Однако невозможно для всех электронов создать одинаковые условия движения. В эксперименте у электронов могут быть различные ВкриIкр. В результате у тока соленоида Iс существует «переходная» область значений, при которых одна часть электронов достигает анода, а другая часть — нет. При этом по мере возрастания тока Iс анодный ток Iа уменьшается. При расчетах можно взять значение критического тока Iкр, соответствующее середине самого крутого участка спада или точке перегиба графика сбросовой характеристики. Это значение будет критическим для наибольшего количества электронов. В центральной части соленоида магнитное поле можно считать однородным и магнитную индукцию рассчитывать как для центральной точки. Тогда

СКАЧАТЬ ЯНДЕКС ДИСКА ОТВЕТЫ

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

где N — число витков в соленоиде; L — его длина; D — диаметр; m0 = 4p · 10–7 Гн/м — магнитная постоянная.

На рисунке: ЭЛ — электронная лампа; С — соленоид; анодное напряжение устанавливается с помощью реостата R и контролируется вольтметром V; анодный ток измеряется миллиамперметром мA. Ток в соленоиде изменяется с помощью переменного сопротивления Rс и измеряется амперметром A. Параметры намотки соленоида: число витков N = 2006; длина L = 167 мм;

диаметр D = 62 мм. Параметры электродов лампы: радиус анода ra = 6 мм; радиус катода rк = 0,3 мм. Порядок выполнения работы 1. Установить анодное напряжение Ua = 50 В и занести в табл. 1 и 2. 2. Изменяя ток в соленоиде Iс от минимального (начального) значения до максимального через 0,1 A, снять сбросовую характеристику (зависимость анодного тока Iа от Iс). Результаты измерений занести в табл. 1. 3. Повторить пп. 2 и 3 при двух других значениях Ua (>50 В). 4. Для каждого значения Ua построить график сбросовой характеристики Iа(Iс), по графику определить критическое значение Iкр и занести в табл. 2. 5. Для каждого значения Iкр рассчитать по формуле (6) критическое значение магнитной индукции Вкр. 6. Для каждой пары Ua и Вкр вычислить по формуле (5) величину удельного заряда электрона е/m и определить среднее значение. 7. Оценить погрешность полученной величины е/m.

СКАЧАТЬ ЯНДЕКС ДИСКА ОТВЕТЫ

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Контрольные вопросы 1. Какие силы действуют на электроны, движущиеся в электрическом и магнитном полях? Как они направлены? 2. В чём суть метода магнетрона для определения отношения e/m? 3. Что такое критическая индукция и как ее определить? 4. Влияет ли на величину Bкр изменение направления тока в соленоиде на противоположное? 5. Зависит ли величина e/m от величины анодного напряжения?

теги: гуап, физика, ответы, лабораторные, методичка, скачать, экзамен, зачет, Санкт-Петербургский государственный университет аэрокосмического приборостроения

Источник

Определение удельного заряда электрона

Лабораторная работа № 5

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА

Ознакомление с одним из методов определения отношения заряда электрона к его массе, основанном на законах движения электрона в электрическом и магнитном полях.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Удельным зарядом частицы называется отношение заряда к массе этой частицы.

Удельный заряд можно определить, исследуя движение частицы в электрическом и магнитном полях. Такие исследования проводились в конце XIX века английским ученым Дж. Дж. Томсоном и привели к открытию электрона.

При движении электрона в поперечных электрическом или магнитном полях возможно определение удельного заряда по отклонению его траектории от первоначального направления.

Электрическое поле с напряженностью Е действует на электрон, находящийся в этом поле с силой

,

где е=–1.6 10–19 Кл – заряд электрона.

Направление этой силы противоположно направлению вектора напряженности электрического поля. Работа, совершаемая этой силой при движении электрона в поле, будет сопровождаться изменением кинетической энергии электрона.

Магнитное поле с индукцией В действует на электрон, движущийся в этом поле с силой , силой Лоренца, которая зависит от величины и направления скорости движения электрона (рис. 1).

Сила магнитного поля – сила Лоренца – равна

, (1)

где е – заряд электрона;

V – скорость электрона;

В – индукция магнитного поля.

Если движение электрона происходит в вакууме (воздухе), то эту силу можно выразить через напряженность магнитного поля Н:

, (2)

где a – угол между вектором напряженности поля и вектором скорости электрона;

m0=12,5×10-7 Гн/м – магнитная постоянная;

m – магнитная проницаемость среды (для вакуума равна 1).

Сила Лоренца перпендикулярна плоскости, в которой лежат векторы и . Направление ее можно определить по известному правилу правого винта (буравчика). На рис. 1 направление силы показано точкой от плоскости чертежа на нас.

Так как сила Лоренца перпендикулярна вектору скорости частицы, то она может изменить не величину, а только направление скорости электрона.

В случае движения электрона по направлению линий индукции маг-нитного поля (sina=0) cила , а при движении перпендикулярно к ним (sina=1) эта сила имеет макси-мальное значение и вызывает движение электрона по окружности (рис. 2).

Если в пространстве, где движется электрон, имеются одновременно электрическое и магнитное поля, то в общем случае будет происходить изменение скорос-ти электрона как по величине, так и по направлению.

Представим себе находящиеся в вакууме металлический цилиндр и металлическую накаливаемую нить, натянутую вдоль оси цилиндра (рис. 3). Если между нитью и цилиндром приложить разность потенциалов так, чтобы нить являлась катодом, а цилиндр положительным анодом, то электроны, вылетающие из нити, будут под действием электрического поля притягиваться к цилиндрическому аноду. Их движение будет прямолинейным и ускоренным. Если дополнительно создать внутри цилиндра однородное магнитное поле, напряженность которого параллельна оси цилиндра, то вылетающие из нити электроны, пересекая магнитное поле, будут двигаться не по радиальным, а по криволинейным траекториям.

Очевидно, что искривление траекторий электронов будет тем больше, чем больше будет действующая на них сила Лоренца, пропорциональная напряженности магнитного поля.

Практически такую установку можно осуществить, поместив электронную лампу с цилиндрическим анодом в соленоид с током.

Нагревая катод и создавая некоторую разность потенциалов U между катодом и анодом, будем пропускать через соленоид постоянный ток, получая тем самым постоянное магнитное поле внутри цилиндра-анода. Тогда на электрон, вылетевший из катода, одновременно будут действовать силы со стороны электрического и магнитного полей.

Электрическая сила направлена по радиусу от катода к аноду. Напряженность электрического поля в некоторой точке х пространства между двумя коаксиальными цилиндрами (катодом и анодом) определяется следующим выражением:

, (3)

где U – разность потенциалов между цилиндрами;

х – расстояние от оси цилиндра до точки, где, определяется напряженность;

r – радиус нити катода;

R – внутренний радиус цилиндрического анода.

Электрон, пролетевший от катода к аноду, приобретает кинетическую энергию, равную работе электрической силы независимо от того, движется ли он по прямой или по любой другой траектории:

. (4)

Сила, действующая со стороны магнитного поля, зависит от напряженности магнитного поля Н внутри соленоида с током. Если соленоид достаточно длинный, то напряженность рассчитывается следующим образом:

, (5)

где I – сила тока в соленоиде;

N – число витков в соленоиде;

1 – длина соленоида.

Магнитное поле искривляет траекторию движения электрона в плоскости, перпендикулярной оси катода и анода (предполагаем, что вылетающие из катода электроны не имеют скорости в направлении оси, в противном случае, траектории электронов будут спиральными). Очевидно, если Н мало, то траектории частиц будут слабо искривлены, и все электроны будут попадать на внутреннюю поверхность анода.

Однако можно создать поле с такой напряженностью, что траектории электронов не пересекут поверхности анода, все электроны вернутся на катод (рис. 4).

Предельное значение напря-женности магнитного поля, при котором прекращается попада-ние электронов на анод, назы-вается критическим .

При напряженности траектория электрона будет круговой с радиусом , который и будет определять нормальное (центростремительное) ускорение, приобретенное электроном под действием электрической и магнитной сил:

.

Тогда на основании (2) и (3) можно записать

. (6)

Учитывая, что величина скорости определяется только электрическим полем (3), получим

, (7)

откуда и получаем удельный заряд электрона:

. (8)

Источник

Введение

Удельным зарядом называется отношение заряда частицы к ее массе е/m.

Определив значение удельного заряда и величину заряда, подсчитывают массу частиц. Таким методом подсчитана масса электрона и других элементарных частиц.

Одним из методов определения удельного заряда является метод магнетрона. Магнетрон представляет собой двухэлектродную лампу, которая помещена в магнитное поле. Анод в этой лампе представляет собой металлический цилиндр, по оси которого натягивается нить накала – катод (рис. 1). При подогреве катода из него вылетают электроны. Вылетевшие из катода электроны образуют вокруг катода «электронное облачко». Если между катодом и анодом создать разность потенциалов, то электроны из облачка устремятся к положительно заряженному аноду. В анодной цепи лампы пойдет ток.

Если двухэлектродную лампу поместить в магнитное поле, то электрон попадет в сложное электромагнитное поле.

Известно, что на заряд, движущийся со скоростью v в магнитном поле с индукцией В, действует сила Лоренца

F = e· v ·B·sinα

Из формулы видно, что величина силы Лоренца зависит не только от значения скорости и индукции магнитного поля, но и от взаимной ориентации векторов v и В.

Сила Лоренца будет равна 0, если заряд будет двигаться вдоль линии индукции магнитного поля, и будет максимальна при движении заряда в направлении, перпендикулярном индукции магнитного поля.

В нашем случае магнетрон помещен внутри соленоида так, что созданное током в его обмотке магнитное поле параллельно оси лампы, т.е. нити накала.

При отсутствии магнитного поля электрон движется строго по радиусу от нагретого катода к аноду (рис. 2а). Если теперь пропустить ток по обмотке соленоида, то во внутренней его части возникает однородное магнитное поле. Сила, действующая на электрон в магнитном поле, отклонить электрон от прямолинейного пути. Путь электрона будет искривлен (рис. 2б). При некотором критическом значении магнитного поля электроны перестанут попадать на анод и будут двигаться по траектории, которую в первом приближении можно представить в виде окружности (рис. 2в).

Радиус этой окружности равен половине радиуса анода магнетрона.

где r – радиус траекторий движения электрона;

При движении электрона по окружности, сила Лоренца, обусловливающая это движение, является центростремительной силой и равна

Сократив обе части равенства на v, получим

(1)

В электрическом поле электрон приобретает скорость за счет разности потенциалов между анодом и катодом U = U_К – U_А. Следовательно

Отсюда можно определить скорость движения электрона

Подставим значение скорости в уравнение (1)

Решая равенство относительно , получим

(2)

Принимая во внимание, что , подставив значение r в формулу (2), получим

(3)

где

Напряженность магнитного поля соленоида определяется по формуле

(4)

Как показывает опыт, даже при малых магнитных полях анодный ток магнетрона начинает падать. Так как магнитное поле не влияет на число вылетевших из нити электронов, то постепенное падение анодного тока можно объяснить тем, что электроны вылетают из катода с различной скоростью и всегда будет некоторое число медленных, которые будут возвращаться на нить, не попадая на анод даже при малых магнитных полях.

При дальнейшем увеличении напряженности магнитного поля наступит такой момент, при котором большинство электронов, имеющих среднюю скорость, будут описывать окружность радиусом R/2 и будут возвращаться на катод. Анодный ток при этом очень быстро падает.

Зависимость анодного тока от силы тока в соленоиде, создающем магнитное поле, представлена на рис. 3. Будем считать, что формула (3) выведена для средней скорости движения электронов. Тогда в формуле Н есть то значение напряженности магнитного поля, при котором на рис. 3 получается точка перегиба.

Описание установки

В качестве магнетрона в данной работе используется кенотрон с радиусом анода R = 1,35 см = 0,0135 м. Эта лампа помещена внутри соленоида.

Обмотка соленоида питается от источника постоянного тока напряжением 50 В. Цепь соленоида собирается по схеме (рис. 4).

Анодное напряжение и напряжение накала катода подается с универсального источника питания УИП-1.

Порядок выполнения работы

1. Изучить рабочую установку.

2. Установить при помощи потенциометра в анодной цепи напряжение порядка 90 В.

Источник