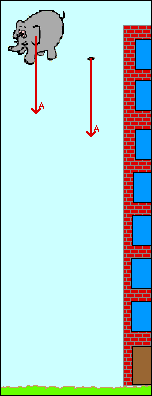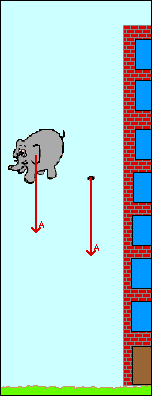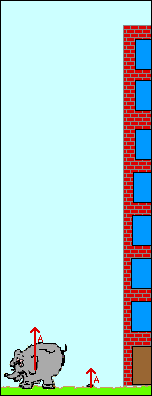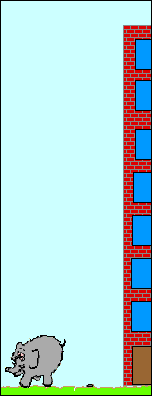
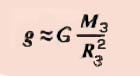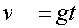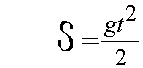Что называется свободным падением
Свободное падение тел
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Так как начальна скорость равна нулю, перепишем:
Отсюда находится выражение для времени падения тела с высоты h :
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
Максимальная высота подъема тела, брошенного вертикально:
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Условия для движения вдоль оси О Х :
Условия для движения вдоль оси O Y :
Приведем формулы для движения тела, брошенного под углом к горизонту.
Дальность полета тела:
Максимальная высота подъема:
Свободное падение тел
Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г.Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Свободное падение является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу в 1.4, положив υ0 = 0, y0 = h, a = –g. Обратим внимание на то, что если тело при падении оказалось в точке с координатой y 0, a = –g. Это дает:
Через время υ0 / g скорость тела υ обращается в нуль, т. е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой
Тело возвращается на землю (y = 0) через время 2υ0 / g, следовательно, время подъема и время падения одинаковы. Во время падения на землю скорость тела равна –υ0, т. е. тело падает на землю с такой же по модулю скоростью, с какой оно было брошено вверх.
Максимальная высота подъема
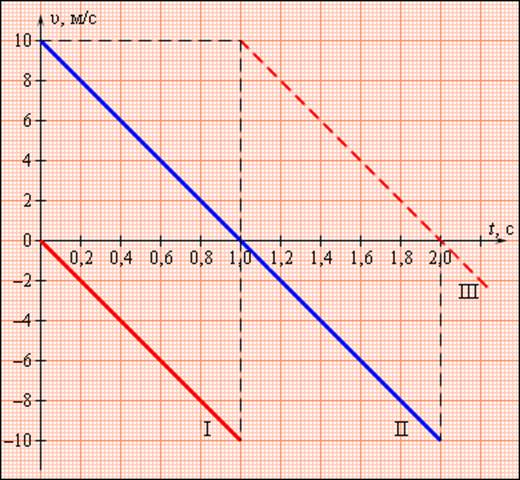
Графики скоростей для различных режимов движения тела с ускорением a = –g
На рис. 1.5.1 представлены графики скоростей для трех случаев движения тела с ускорением a = –g. График I соответствует случаю свободного падения тела без начальной скорости с некоторой высоты h. Падение происходило в течение времени tп = 1 с. Из формул для свободного падения легко получить: h = 5 м (все числа в этих примерах округлены, ускорение свободного падения принято равным 10 м/с 2 ).
График II – случай движения тела, брошенного вертикально вверх с начальной скоростью υ0 = 10 м/с. Максимальная высота подъема h = 5 м. Тело возвращается на землю через время t = 2 с.
График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II.
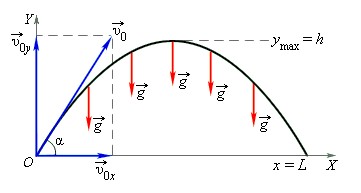
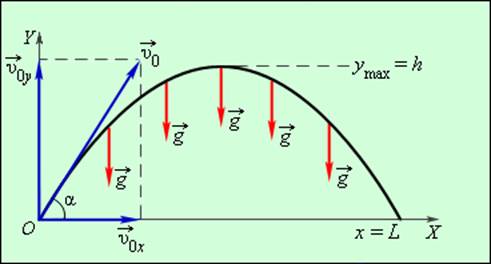
Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. На рис. 1.5.2 изображен вектор начальной скорости 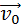
Движение тела, брошенного под углом 
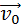
Таким образом, для движения вдоль оси OX имеем следующие условия:
а для движения вдоль оси OY
Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом α к горизонту.
Время полета:
Дальность полета:
Максимальная высота подъема:
Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.
Вопросы.
1. Что называется свободным падением тел?
Движение тела под действием силы тяжести называется свободным падением.
2. Как доказать, что свободное падение шарика, изображенного на рисунке 27, было равноускоренным?
Если модули векторов перемещения ISI пройденного шариком за последовательные промежутки времени t будут относится как S1: S2: S3. = 1 : 3 : 5. то это будет служить доказательством того, что падение происходит с одинаковым ускорением (см. § 8, 4 вопрос).
3. С какой целью ставился опыт, изображенный на рисунке 28, и какой вывод из него следует?
Опыт ставился с целью: определить, зависит ли ускорение свободного падения от массы, формы, материала и т.п. свойств тел. Из этого опыта может быть сделан вывод, что ускорение свободного падения для всех тел одинаково.
4. Что такое ускорение свободного падения?
5. Почему в воздухе кусочек ваты падает с меньшим ускорением, чем железный шарик?
При падении тела в воздухе на него действует сила сопротивления воздуха. Кусочек ваты падает медленнее так как например при одинаковом размере железного шарика и кусочка ваты, первый будет намного тяжелее второго, и вклад силы сопротивления в результирующую силу будет значительно больше для кусочка ваты, чем для железного шарика.
6. Кто первым пришел к выводу о том, что свободное падение является равноускоренным движением?
Существует легенда, что Галилео Галилей сбрасывал металлические шары разной массы с Пизанской башни. Однако падение было слишком быстрым и Галилей проделал опыты по скатыванию шаров по наклонной плоскости, чтобы увеличить время падения.
1. С какой высоты свободно падала сосулька, если расстояние до земли она преодолела за 4с?
2. Определите время падения монетки, если её выронили из рук на высоте 80 см над землей (g = 10 м/с 2 ).
3. Маленький стальной шарик упал с высоты 45м. Сколько времени длилось его падение? Какое перемещение совершил шарик за первую и последнюю секунды своего движения? (g = 10 м/с 2 ).
Что называется свободным падением
Свободное падение тел.
Свободным падением называют падение тел в безвоздушном пространстве (вакууме) из состояния покоя (т. е. без начальной скорости) под действием притяжения Земли.
Падение тел является свободным лишь в том случае, когда на падающее тело действует только сила тяжести. Падение тел в воздухе можно приближенно считать свободным лишь при условии, что сопротивление воздуха мало и им можно пренебречь.
Свободное падение тел впервые исследовал Галилей, который установил, что свободно падающие тела движутся равноускоренно с одинаковым для всех тел ускорением.
В вакууме все тела независимо от их масс падают с одинаковым ускорением.
Ускорение свободного падения
В условиях идеального падения падающие с одинаковой высоты тела достигают поверхности Земли, обладая одинаковыми скоростями и затрачивая на падение одинаковое время.
При идеальном свободном падении тело возвращается на Землю со скоростью, величина которой равна модулю начальной скорости.
Время падения тела равно времени движения вверх от момента броска до полной остановки в наивысшей точке полета.
Только на полюсах Земли тела падают строго по вертикали. Во всех остальных точках планеты траектория свободно падающего тела отклоняется к востоку за счет силы Кариолиса, возникающей во вращающихся системах (т.е. сказывается влияние вращения Земли вокруг своей оси).
Движение с постоянным ускорением свободного падения
Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Когда начальная скорость точки равна нулю или же направлена вдоль той же прямой, что и ускорение, то точка движется прямолинейно вдоль этой прямой. Если начальная скорость и ускорение не направлены по одной прямой, точка движется криволинейно.
Свободное падение
В частности, парашютист в течение нескольких первых секунд прыжка находится практически в свободном падении.
Свободное падение возможно на поверхность любого тела, обладающего достаточной массой (планеты и их спутники, звёзды, и т. п.).
Во время свободного падения какого-либо объекта этот объект находится в состоянии невесомости (как если бы он находился на борту космического аппарата, движущегося по околоземной орбите). Данное обстоятельство используется, например, при тренировке космонавтов: самолёт с космонавтами набирает большую высоту и пикирует, находясь в течение нескольких десятков секунд в состоянии свободного падения; космонавты и экипаж самолёта при этом испытывают состояние невесомости.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Теоре́ма промежу́точной оси́, или теоре́ма те́ннисной раке́тки в классической механике — утверждение о неустойчивости вращения твёрдого тела относительно второй главной оси инерции. Является следствием законов классической механики, описывающих движение твёрдого тела с тремя различными главными моментами инерции. Проявление теоремы при вращении такого тела в невесомости часто называют эффектом Джанибекова, в честь советского космонавта Владимира Джанибекова, который заметил это явление 25 июня.
Механи́ческим движе́нием тела называется изменение его положения в пространстве относительно других тел с течением времени. При этом тела взаимодействуют по законам механики.
В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).
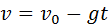
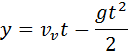
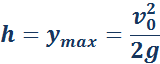
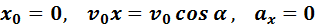
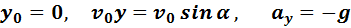
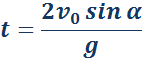
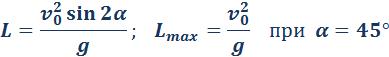
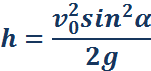



.jpg)