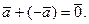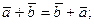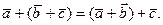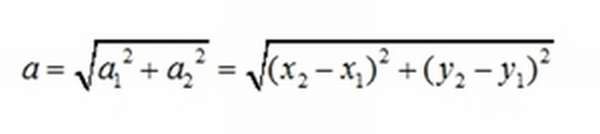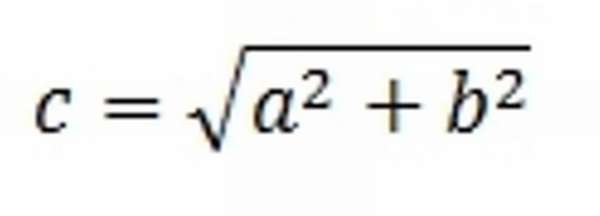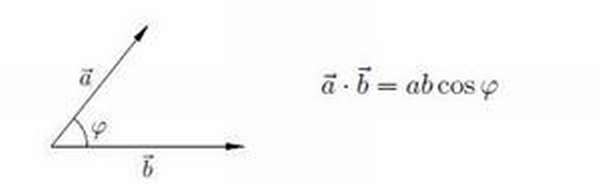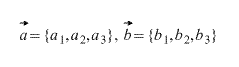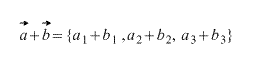Что называется суммой двух векторов
Сумма векторов
Определение. Суммой векторов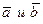 
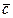
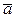
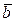
называется такой вектор 
, начало которого совпадает с началом вектора 
, а конец – с концом вектора 
(правило треугольника).
Из определения следует, что сумма двух противоположных векторов равна нулевому вектору: 
Сложение векторов подчиняется следующим законам:
а) переместительному закону
б) сочетательному закону
Операция сложения может быть распространена на любое число слагаемых векторов.
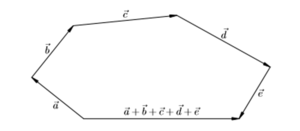
Для того чтобы сложить n векторов, надо к концу первого вектора приложить начало второго, затем к концу второго вектора приложить начало третьего и т.д. и, наконец, приложить к концу предпоследнего вектора начало последнего; тогда замыкающий вектор, соединяющий начало первого вектора с концом последнего, и будет являться вектором-суммой данных векторов.
При сложении векторов можно любым образом переставлять и группировать слагаемые.
Какой вектор называется суммой двух векторов
Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.
В геометрии и физике есть величины, характеризующиеся и числовым значением, и направлением.
Их целесообразно изображать направленными отрезками или векторами.
У таких величин есть начало (отображается точкой) и конец, обозначаемый стрелкой. Длина отрезка называется модулем (длиной).
Это интересно: как переводить градусы в радианы?
Координаты на плоскости
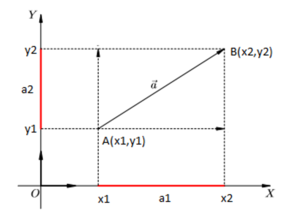
Зададим на плоскости отрезок, направленный из точки, А (x1,y1) в точку В (x2,y2). Его координатами a (a1, a2) являются числа а1=x2-x1, а2=y2-y1.
Модуль рассчитывается по теореме Пифагора: 
У нулевого вектора начало совпадает с концом. Координаты и длина равны 0.
Сумма векторов
Существуют несколько правил для расчета суммы
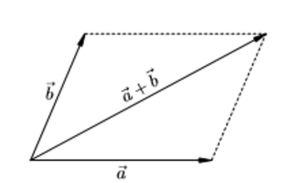
Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.
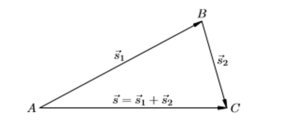
Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.
Результат двух перемещений или их сумма s = s1+ s2. Такой способ называется правилом треугольника.
Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».
Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).
Сумма параллельных (коллинеарных) векторов также определяется по правилу треугольника.
Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.
Примеры:
Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»
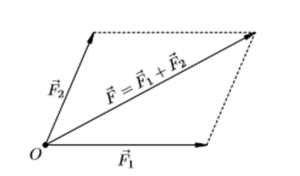
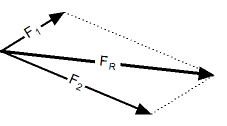
Предположим, что к точечному телу приложены силы F1 и F2.
Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.
Длина в этом случае вычисляется по формуле
, где θ угол между сторонами.
Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.
Обратите внимание: что такое луч в геометрии.
Элементы алгебры
Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:
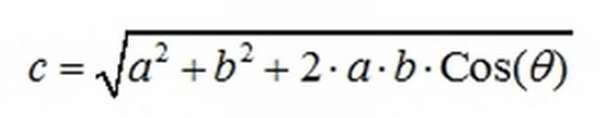
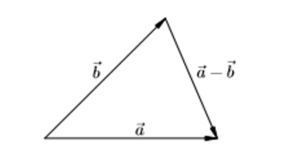
Для вычитания можно использовать видоизмененное правило треугольника.
Умножение на скаляр
Результатом умножения на скаляр будет вектор.
Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.
Скаляр — числовая величина со знаком плюс или минус, больше или меньше единицы.
Примеры скалярных величин в физике:
Примеры:
Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.
Пример:
Сложение и вычитание векторов
Существование: Имеем два следующих случая:
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
Такая операция выполняется по правилу многоугольника.
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора \( \overrightarrow \) выполняется равенство
Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.
Разность векторов. Вычитание векторов
Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)
Умножение вектора на число
Определение Произведением вектора \( \overrightarrow
Длина вектора \( \overrightarrow
Векторы \( \overrightarrow
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.
Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор
Покоординатное сложение векторов.
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов:
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
Правило параллелограмма. Сложение векторов по правилу параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
Правило треугольника. Сложение векторов по правилу треугольника.
Сложение векторов по правилу треугольника заключается в следующем:
Тригонометрический способ. Сложение векторов тригонометрическим способом.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Угол между результирующей силой и первой силой равен:
А угол между второй и результирующей силой можно посчитать следующим образом: as
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Консультации и техническая
поддержка сайта: Zavarka Team
Сложение векторов — свойства, правила и примеры решения задач
Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Сложение координат
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).
Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:
Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.
Правило параллелограмма
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.
Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.
Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.
Альтернативные методы
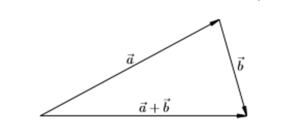
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
При сложении нескольких векторов удобно выполнять следующую последовательность построений:
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.
Следует отметить, что методы используются только, если направление отрезков является сонаправленным.
Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.