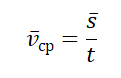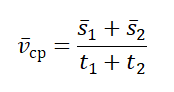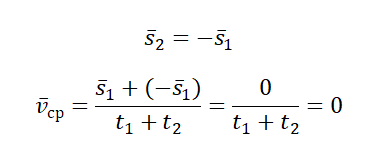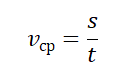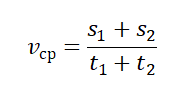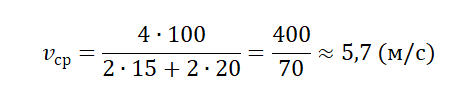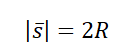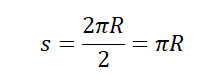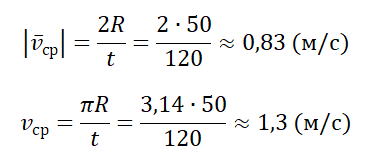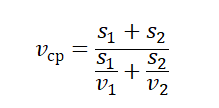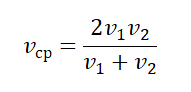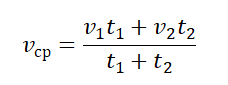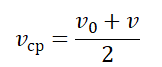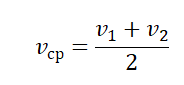Что называется средней скоростью перемещения что такое
Средняя скорость
Сре́дняя ско́рость — в кинематике некая усреднённая характеристика скорости частицы за время её движения. Различают два основных определения средней скорости.
Средняя путевая скорость
Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:
Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.
Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.
В то же время если, например, половину пути автомобиль двигался со скоростью 180 км/ч, а вторую половину со скоростью 20 км/ч, то средняя скорость будет 36 км/ч. В примерах, подобных этому, средняя скорость равна среднему гармоническому всех скоростей на отдельных, равных между собой, участках пути.
Средняя скорость по перемещению
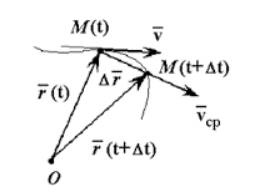
Можно также ввести среднюю скорость по перемещению, которая будет вектором, равным отношению перемещения ко времени, за которое оно совершено:
Средняя скорость, определённая таким образом, может равняться нулю даже в том случае, если точка (тело) реально двигалась (но в конце промежутка времени вернулась в исходное положение).
Если перемещение происходило по прямой (причём в одном направлении), то средняя путевая скорость равна модулю средней скорости по перемещению.
Полезное
Смотреть что такое «Средняя скорость» в других словарях:
средняя скорость U, м/с — 3.1.9 средняя скорость U, м/с: Средняя осевая скорость, определяемая отношением объемной подачи, к площади поперечного сечения трубы или любого иного поперечного сечения А проточной части: … … Словарь-справочник терминов нормативно-технической документации
средняя скорость — vidutinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Aritmetinis greičių vidurkis. atitikmenys: angl. average speed; mean velocity vok. Durchschnittsgeschwindigkeit, f; mittlere Geschwindigkeit, f rus. средняя скорость, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
средняя скорость — vidutinis greitis statusas T sritis fizika atitikmenys: angl. average speed; mean velocity vok. Durchschnittsgeschwindigkeit, f; mittlere Geschwindigkeit, f rus. средняя скорость, f pranc. vitesse moyenne, f … Fizikos terminų žodynas
средняя скорость — vidutinis greitis statusas T sritis ekologija ir aplinkotyra apibrėžtis Aritmetinis tam tikro reiškinio, vyksmo ar prietaiso, mašinos darbo arba veiksmo greičio vidurkis. atitikmenys: angl. average velocity; mean velocity vok. mittlere… … Ekologijos terminų aiškinamasis žodynas
средняя скорость — vidutinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Per pratybas arba varžybas įveikto nuotolio, jo dalių ilgio ir sugaišto laiko santykis. Pavyzdžiui, jeigu irkluotojas 1000 m nuotolyje sugaišo 4 min., vidutinis greitis =1000 … Sporto terminų žodynas
Средняя скорость фильтрования — 55. Средняя скорость фильтрования Величина, численно равная отношению объема фильтрата, получаемого с единицы поверхности фильтрования, ко времени собственно фильтрования Источник: ГОСТ 16887 71: Разделение жидких нео … Словарь-справочник терминов нормативно-технической документации
средняя скорость течения жидкости. — 3.13.10 средняя скорость течения жидкости. Средняя скорость: Условная скорость, равная отношению расхода к площади живого сечения. Источник: СО 34.21.308 2005: Гидротехника. Основные понятия. Термины и определения … Словарь-справочник терминов нормативно-технической документации
средняя скорость изменения напряжения возбуждения — 3.28 средняя скорость изменения напряжения возбуждения: Скорость изменения напряжения системы возбуждения или возбудителя турбогенератора (гидрогенератора, синхронного компенсатора), вычисленная заменой фактической кривой изменения напряжения… … Словарь-справочник терминов нормативно-технической документации
средняя скорость плавания — vidutinis plaukimo greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Plaukiko greitis visame nuotolyje, atmetus laiką, sugaištą starto ir posūkio nuotoliams įveikti. Pavyzdžiui, vyrų 100 m plaukimo laisvuoju stiliumi varžybose starto… … Sporto terminų žodynas
средняя скорость возможных столкновений — 3.12 средняя скорость возможных столкновений: Среднее значение относительной скорости, полученное усреднением относительных скоростей всех КО, с которыми может столкнуться заданный КО, т.е. усреднением по множеству возможных столкновений.… … Словарь-справочник терминов нормативно-технической документации
Мгновенная и средняя скорость
Если материальная точка находится в движении, то ее координаты подвергаются изменениям. Этот процесс может происходить быстро или медленно.
Величина, которая характеризует быстроту изменения положения координаты, называется скоростью.
Мгновенная скорость точки. Формулы
Мгновенная скорость характеризует движение в определенный момент времени. Выражение «скорость тела в данный момент времени» считается не корректным, но применимым при математических расчетах.
Мгновенной скоростью называют предел, к которому стремится средняя скорость » open=» υ при стремлении промежутка времени ∆ t к 0 :
Имеющееся выражение υ = l i m ∆ t ∆ r ∆ t = d r d t = r ˙ в декартовых координатах идентично ниже предложенным уравнениям:
Перемещение и мгновенная скорость
Запись модуля вектора υ примет вид:
Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением d r = υ ( t ) d t
Решение
Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:
Решение
Вычислим уравнение мгновенной скорости, подставим числовые выражения:
Что называется средней скоростью перемещения что такое
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.
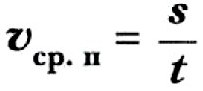
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения 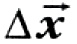
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.
Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»
Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
I. Механика
Тестирование онлайн
Виды неравномерного движения
Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.
Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.
Мгновенная скорость
Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Средняя скорость

У средних величин рисуют сверху горизонтальную черту.
Средняя скорость перемещения. Средняя путевая скорость
Главное запомнить
1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения
Формула для определения средней скорости*
Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.
Определение мгновенной скорости графически*
Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
Поезд прошел путь между городами со скоростью 50км/ч. Какая это скорость: средняя или мгновенная?
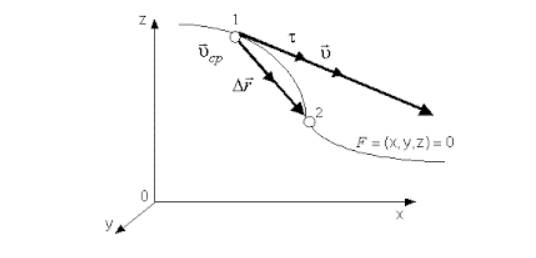
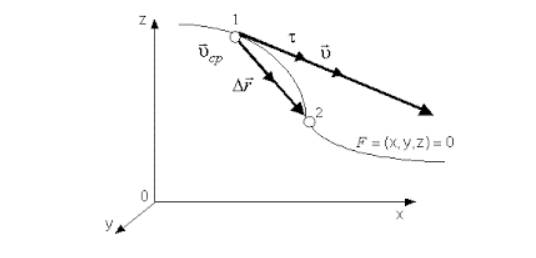
*Два шарика начали одновременно и с одинаковой скоростью двигаться по поверхностям, имеющим форму, изображенную на рисунке. Как будут отличаться скорости и время движения шариков к моменту их прибытия в точку В? Силу трения не учитывать.
Задача решается графическим способом. Скорости будут одинаковы. Время движения второго шарика меньше. Примерные графики движения шариков приведены на рисунке. Так как пути. пройденные шариками, равны, то, как видно из графика (на графике пути численно равны площадям заштрихованных фигур), время второго шарика меньше времени первого.
Неравномерное движение и средняя скорость
теория по физике 🧲 кинематика
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
v ср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому: