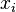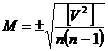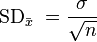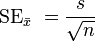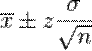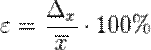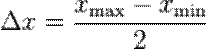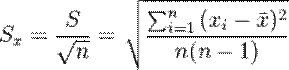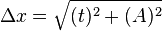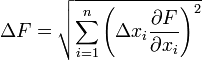Что называется средней квадратичной погрешностью
Виды погрешностей. Средняя квадратическая погрешность



Виды погрешностей. Практически всегда погрешность включает в себя две составляющие ее части: систематическую и случайную.
Систематической называется погрешность, которая в данных условиях сохраняет постоянное значение (или изменяется, но по известному закону).
Такие погрешности вызваны постоянно действующими причинами, в результате чего при измерении мы каждый раз «ошибаемся» на одну и ту же величину. Очень часто такие погрешности вызваны неточным изготовлением прибора (инструментальные погрешности), или постоянным внешним фактором. Например, собственное магнитное поле самолета вызывает погрешность измерения магнитного курса (девиацию), которая на каждом курсе имеет вполне определенное значение.
Систематические погрешности, поскольку они одинаковы при каждом измерении, можно один раз определить с помощью более точных приборов, а затем исключать их из результатов измерений путем ввода поправок.
Систематические погрешности не доставляют особых хлопот при навигации, поскольку после их устранения они уже отсутствуют. Поэтому далее будем считать, что систематические погрешности отсутствуют (уже учтены).
Случайная погрешность при каждом измерении принимает разное значение, причем заранее неизвестно какое именно.
А вот случайные погрешности в принципе устранить нельзя, поскольку они при каждом измерении различны. И они всегда остаются неизвестными.
Определить численные значения случайных погрешностей невозможно, однако пилот постоянно должен иметь в виду, что эти погрешности существуют и иметь представление об их возможных значениях. Наличие неопределенности в результатах измерений является одним из основных факторов, усложняющих навигацию и делающих ее не только наукой, и искусством.
Случайным событием называют событие, которое при данных условиях может произойти или не произойти. Степень возможности наступления такого события численно характеризуют величиной вероятности. Вероятность Р – это число, которое может лежать в пределах от 0 до 1. Если при данных условиях событие никогда не происходит, его называют невозможным событием и его вероятность равна нулю. Если же оно при данных условиях происходит всегда, то его называют достоверным и приписывают ему вероятность равную единице. Если, например, Р=0,3, то это означает, что в среднем в 30 случаях из 100 событие произойдет. Именно в среднем, поскольку событие является случайным. Если создать необходимые для наступления события условия и провести серию из 100 опытов, то событие может произойти, например, 23 раза, или 32 раза… Если провести несколько серий таких опытов, или одну серию из тысячи, десяти тысяч, миллиона опытов, то, чем большее количество опытов проведено, тем ближе среднее количество наступлений события будет ближе к 30% от общего количества опытов (если Р=0,3).
Каким же образом можно описать случайные погрешности, если они не имеют какого-либо определенного значения? Часто их характеризуют величиной средней квадратической погрешности (СКП), которая обозначается буквой σ (сигма). Так, например, СКП измерения величины a будем обозначать σa.
СКП является характеристикой степени рассеяния измеренного значения величины вокруг фактического ее значения. Чем больше σa, тем больше рассеяны (разбросаны) измеренные в разных опытах значения вокруг фактического значения величины.
На рис. 2.19 геометрически представлены в виде числовой оси возможные значения измеряемой величины a и отмечено фактическое ее значение. Крестиками на шкале обозначены полученные в результате нескольких опытов измеренные значения. В первом случае разброс измеренных значений вокруг фактического больше, чем во втором случае, следовательно «сигма», которая и характеризует степень разброса, во втором случае меньше.
Рис. 2.19. Средняя квадратическая погрешность
По величине СКП можно судить о вероятностях того, что измеренное значение примет то или иное значение. Но для этого недостаточно знать СКП, нужно также знать, какому закону распределения подчиняется данная случайная погрешность. Многие случайные величины подчиняются нормальному (гауссовскому) закону распределения. Для этого закона полезно запомнить следующие значения.
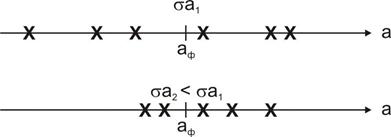
Если систематическая погрешность отсутствует и в результате измерения получено значение aизм, то фактическое значение величины лежит в пределах (рис. 2.20):
aизм ± σa с вероятностью Р=0,68;
aизм ± 2σa с вероятностью Р=0,95;
aизм ± 3σa с вероятностью Р=0,997.
Рис. 2.20. Некоторые вероятности для нормального закона распределения
в 68 случаях из 100 лежит в пределах 100º ±2º, то есть в интервале 98º…102 º;
в 95 случаях из 100 лежит в пределах 100º ±4º, то есть в интервале 96º…104º;
в 997 случаях из 1000 лежит в пределах 100º ±6º, то есть в интервале 94º …106º.
Значение вероятности Р=0,997 настолько близко к единице, что соответствующее ей значение погрешности в «три сигмы» часто называют максимальной погрешностью. На самом деле погрешность может его и превысить. Правда, редко – в среднем в трех случаях из тысячи.
Соответственно, в пяти случаях из ста погрешность может быть и больше. Для нормального закона распределения погрешности вероятность 0,95 соответствует удвоенной СКП. Следовательно, СКП измерения пеленга в данном примере составит 0,75º.
Погрешность средняя квадратическая
Смотреть что такое «Погрешность средняя квадратическая» в других словарях:
средняя квадратическая погрешность уравненного значения (результата геодезических измерений) — 3.7.11 средняя квадратическая погрешность уравненного значения (результата геодезических измерений) <тx0>Оценка значения геодезической величины по результатам уравнивания измерений, получаемая по формуле где mQ средняя квадратическая погрешность … Словарь-справочник терминов нормативно-технической документации
средняя квадратическая погрешность результата измерений — aritmetinio vidurkio vidutinė kvadratinė paklaida statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. root sum square error vok. mittlerer quadratischer Fehler, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
средняя квадратическая погрешность результата (геодезических) измерений — 3.6.13 средняя квадратическая погрешность результата (геодезических) измерений; СКП <т>Эмпирическая оценка среднего квадратического отклонения результата измерений. Примечание: Оценка т погрешности отдельного результата геодезических измерений… … Словарь-справочник терминов нормативно-технической документации
интегральная средняя квадратическая погрешность телеметрирования — Показатель, характеризующий среднюю квадратическую погрешность телеметрирования на наблюдаемом интервале времени и равный корню квадратному из результата усреднения квадрата погрешности как по времени, так и по множеству реализаций. [ГОСТ 19619… … Справочник технического переводчика
Интегральная средняя квадратическая погрешность телеметрирования — 54. Интегральная средняя квадратическая погрешность телеметрирования Е. Integral mean square error of telemetering Показатель, характеризующий среднюю квадратическую погрешность телеметрирования на наблюдаемом интервале времени и равный корню… … Словарь-справочник терминов нормативно-технической документации
Интегральная средняя квадратическая погрешность телеметрирования — 1. Показатель, характеризующий среднюю квадратическую погрешность телеметрирования на наблюдаемом интервале времени и равный корню квадратному из результата усреднения квадрата погрешности как по времени, так и по множеству реализаций… … Телекоммуникационный словарь
Погрешность — 10. Погрешность По title= РМГ 29 99 ГСИ. Метрология. Основные термины и определения Источник: ГОСТ 12.1.016 79: Система станд … Словарь-справочник терминов нормативно-технической документации
Средняя — периодическое увлажнение пола, при котором поверхность покрытия пола влажная или мокрая; покрытие пола пропитывается жидкостями. Источник: МДС 31 12.2007: Полы жилых, общественных и производственных зданий с применением м … Словарь-справочник терминов нормативно-технической документации
Погрешность измерения — Сюда перенаправляется запрос «Относительная точность». На эту тему нужна отдельная статья. Сюда перенаправляется запрос «Абсолютная то … Википедия
Погрешность — измерения оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины… … Википедия
Средняя квадратическая погрешность. Предельная и относительная погрешность.
Предельной погрешностью называют такое наибольшее по абсолютной величине значение случайной ошибки, которой она может достигнуть при данных условиях измерений. Установлено, что случайная ошибка может достигать удвоенной средней квадратической ошибки в пяти случаях из ста, утроенной – в трех из тысячи. Поэтому за предельную ∆пр. принимают утроенную среднюю квадратическую ошибку ∆пр. = 3m.
Относительной ошибкой называют отношение абсолютной ошибки к измеренной величине. Она выражается простой дробью, числитель которой равен единице. Обычно относительной ошибкой характеризуют линейные измерения.
Например, измерена линия длиной l=221,16 с абсолютной ошибкой ∆=0,11 м.
Средняя квадратическая погрешность арифметической средины.
Арифметическая средина является наиболее надежным результатом из многократных измерений. Ее точность характеризуется ошибкой, величина которой должна быть меньше заданной величины, чем количество измерений.
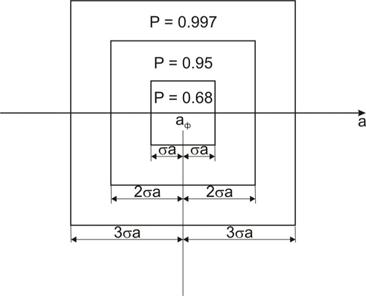
Средняя квадратическая погрешность арифметической средины определяется по формуле
 |
Оценка точности по вероятнейшей погрешности.
В большинстве случаев истинное значение измеряемой величины не известно, поэтому для вычисления средней квадратической ошибки используют отклонения результатов измерений от их среднего арифметического. Эти отклонения называют вероятнейшими погрешностями.
Для вычисления средней квадратической погрешности по вероятнейшим вычисляют разности между каждым результатом измерения и арифметической срединой Х0, эти разности возводят в квадрат и получают среднюю квадратическую погрешность по формуле Бесселя
[l] – nХ0 = [V], Суммарное уравнение,
Но n ≠ 0, следовательно [V] = 0.
Среднюю квадратическую погрешность арифметической средины по вероятнейшим ошибкам определяют по формуле

Среднюю квадратичную ошибку результата по разностям двойных измерений вычисляют по формуле:
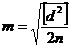
Неравноточные измерения.
Измерения могут быть равноточные и неравноточные. Неравноточными называются измерения одной и той же величины, которые выполняют разными приборами или исполнителями. По разным технологиям или в различных условиях. Неравноточные измерения имеют разный вес, тогда как равноточные измерения имеют одинаковый вес, т.е.степень доверия к результату.
Весом Р называют отношение целого числа С к квадрату средней квадратической погрешности
Из полученных неравноточных измерений, зная их вес, получают общую арифметическую средину или весовое среднее L0 по формуле
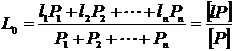
Пример 1. Линия измерена два раза и получили первый раз среднее арифметическое l1 = 212,45 с весом Р = 2.
Вторично эту же линию измеряли четыре раза и нашли среднее арифметическое l2 = 212,38 с весом Р = 4, тогда
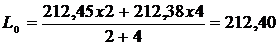
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Средняя квадратическая погрешность
Вот и еще одна средняя, которая связана с погрешностями.
Средняя квадратическая погрешность (СКП) является мерой точности результатов измерений либо функций измеренных величин и является вероятностной характеристикой.
Рис. 3.1. Нормальный закон распределения
— для диапазона ±m ® Р = 68,3% (» 68%);
— для диапазона ±2m® Р = 95,5% (» 95%);
— для диапазона ±3m® Р = 99,7% (практически 100%).
Таким образом, только в 3-х случаях из 1000 может появиться погрешность, превышающая значение 3m. Погрешности, по абсолютной величине превышающие 3m (предельную погрешность), принято считать грубыми, и результаты измерений, содержащие эту грубую погрешность, исключают из дальнейшей обработки. В некоторых случаях, для ужесточения требований к точности измерений, устанавливают предельную погрешность в диапазоне от 2m до 3m.
Значения коэффициента Стьюдента (t) для различных вероятностей (Р)
| t | P% | t | P% | t | P% |
| 0,1 | 8,0 | 1,1 | 72,9 | 2,1 | 96,4 |
| 0,2 | 15,9 | 1,2 | 77,0 | 2,2 | 97,2 |
| 0,3 | 23,6 | 1,3 | 80,6 | 2,3 | 97,9 |
| 0,4 | 31,1 | 1,4 | 83,8 | 2,4 | 98,4 |
| 0,5 | 38,3 | 1,5 | 86,6 | 2,5 | 98,8 |
| 0,6 | 45,1 | 1,6 | 89,0 | 2,6 | 99,1 |
| 0,7 | 51,6 | 1,7 | 91,1 | 2,7 | 99,3 |
| 0,8 | 57,6 | 1,8 | 92,8 | 2,8 | 99,5 |
| 0,9 | 63,2 | 1,9 | 94,3 | 2,9 | 99,6 |
| 1,0 | 68,3 | 2,0 | 95,5 | 3,0 | 99,7 |
Часто значение СКП указывают с коэффициентом t (коэффициент Стьюдента), который и определяет доверительный вероятностный интервал (х ± tm) результата измерений при установленном уровне вероятности Р. Для этого удобно пользоваться табл. 3.1.
Например, необходимо определить доверительный интервал для величины Х с вероятностью 90%. По таблице интерполированием находим, что для Р1 = 89,0% t1 = 1,6, для Р2 = 91,1% t2 = 1,7: tх = 1,6476 » 1,65.
Это значит, что результат измерений с вероятностью 90% находится в пределах (Х ± 1,65 m).
Если измеряемая величина Х известна, то значение СКП определяется по формуле Гаусса:
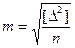
Напомним, что знак [. ] – это знак гауссовой суммы.
Для случаев, когда измеряемая величина неизвестна, используется формула Бесселя:

Как видно из формул (3.9) и (3.10), в случае, когда измеряемая величина известна, для оценки точности достаточно уже одного измерения (оно и является необходимым). Как уже указывалось выше, чаще всего формулу Гаусса используют при оценках точности эталонируемых приборов при измерении известных величин (эталонов). Для оценки точности по формуле Бесселя необходимыми являются как минимум два измерения. Формула Бесселя используется при оценках точности результатов массовых (многократных) измерений одной величины, заранее неизвестной.
При возрастании числа измерений значения СКП, полученные по формулам Гаусса и Бесселя, становятся практически одинаковыми (примерно с n ³ 20). При этом значение СКП одного измерения стремится к пределу mпред, который определяется точностью прибора, точностью метода или программы измерений. Очевидно, выше об этом уже было сказано, что на практике невозможно, да и нецелесообразно по ряду причин, обеспечивать весьма большое число измерений одной величины. При этом практическое число измерений должно обеспечивать получение результата измерения с заданной точностью при установленном уровне доверительной вероятности.
Поскольку число измерений является ограниченным, то сама СКП содержит погрешность, определяемую по приближенной формуле:

Она так и называется – средняя квадратическая погрешность средней квадратической погрешности (СКП СКП).
Здесь уместно возвратиться к классификации погрешностей. Не все виды погрешностей рассмотрены нами выше.
Часто при исследованиях рядов погрешностей измерений используют т.н. вероятную погрешность, которую обозначают буквой r. Величина вероятной погрешности может быть оценена по приближенной формуле

в предположении, конечно, что распределение погрешностей подчиняется нормальному закону.
Вероятную погрешность называют еще срединной погрешностью. Если не хочется делать вычисления по формуле (3.12), потому что в неё входит значение m, которое необходимо получить по формуле Бесселя, то можно определить вероятную или срединную погрешность, расположив ряд погрешностей по их возрастанию по абсолютным величинам. В середине полученного ряда и будет находиться значение этой погрешности. Это если число погрешностей нечётное. А если оно чётное, то срединной погрешностью будет среднее значение соседних погрешностей в середине ряда.
Не надо путать срединную погрешность со средней погрешностью vo, которую можно получить тоже по простой формуле:

Здесь также требуется условие подчинения ряда измерений (погрешностей) нормальному закону.
Средняя погрешность является математическим ожиданием абсолютных значений отклонений результатов измерений какой-либо величины от математического ожидания для этих результатов. Приближенно значение средней погрешности можно оценить по формуле:

где vi – уклонения результатов измерений от их среднего арифметического.
Часто формулу (3.13) используют для предварительной оценки средней квадратической погрешности:

Среднеквадратическая погрешность
Класс точности СИ
Класс точности— основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.
Погрешность может нормироваться, в частности, по отношению к:
результату измерения (по относительной погрешности);
длине (верхнему пределу) шкалы прибора (по приведенной погрешности).
Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.
Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.
Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.
Погрешность измерения —отклонение измеренного значения величины от её истинного (действительного) значения. Погрешность измерения является характеристикой точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение никакой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99 термин ошибка измерения не рекомендуется применять как менее удачный). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины хд, то есть значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него. Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью.
Доверительным называется интервал, который с заданной надежностью покрывает оцениваемый параметр.
Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, более предпочтительной при небольшом объёме выборки, чем точечная. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.
Доверительным интервалом параметра 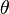
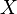
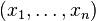
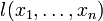
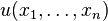
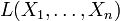
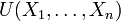
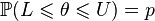
Граничные точки доверительного интервала 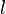
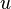
Стандартная ошибка среднего в математической статистике — величина, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке размера 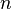
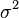
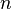
Стандартная ошибка среднего вычисляется по формуле:
где 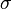
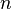
Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле:
где 
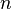
Пример использования: «средний рост студента первого курса составляет 180 ± 20 см с вероятностью 95 %»
180 см — среднее значение выборки;
95 % — доверительная вероятность (коэффициент надёжности);
160—200 см — доверительный интервал;
20 см — предел погрешности.
Толкование: «с вероятностью 95 % истинное среднее значение генеральной совокупности лежит в интервале 160—200 см»
Для нормального распределения:
где, 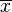
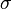
Пределом относительной погрешности называют величину:
Среднеквадратическая погрешность
Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
Средняя квадратическая погрешность среднего арифметического:
По форме представления
Абсолютная погрешность — 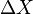
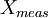
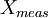
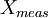
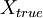

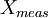
Существует несколько способов записи величины вместе с её абсолютной погрешностью.
Обычно используется запись со знаком ±. Например, рекорд в беге на 100 метров, установленный в 1983 году, равен 9,930±0,005 с.
Для записи величин, измеренных с очень высокой точностью, используется другая запись: цифры, соответствующие погрешности последних цифр мантиссы, дописываются в скобках. Например, измеренное значение постоянной Больцмана равно 1,3806488(13)×10 −23 Дж/К, что также можно записать значительно длиннее как 1,3806488×10 −23 ±0,0000013×10 −23 Дж/К
Относительная погрешность — погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или среднему значению измеряемой величины (РМГ 29-99):
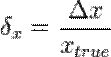
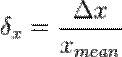
Относительная погрешность является безразмерной величиной; её численное значение может указываться, например, в процентах.
Приведённая погрешность — погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле 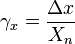
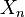
если шкала прибора односторонняя, то есть нижний предел измерений равен нулю, то 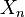
если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведённая погрешность также является безразмерной величиной.
По причине возникновения
Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определённой заранее заданной точностью — основной погрешностью, допускаемой в нормальных условиях эксплуатации для данного прибора. В различных областях науки и техники могут подразумеваться различные стандартные (нормальные) условия (например, Национальный институт стандартов и технологий США за нормальную температуру принимает 20 °C, а за нормальное давление — 101,325 кПа); кроме того, для прибора могут быть определены специфические требования (например, нормальное рабочее положение). Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора — например, температурная (вызванная отклонением температуры окружающей среды от нормальной), установочная (обусловленная отклонением положения прибора от нормального рабочего положения), и т. п.
Обобщённой характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведённых основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)×10n, где показатель степени n = 1; 0; −1; −2 и т. д.
По характеру проявления
Случайная погрешность — составляющая погрешности измерения, изменяющаяся случайным образом в серии повторных измерений одной и той же величины, проведенных в одних и тех же условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их влияние обычно можно устранить статистической обработкой. Описание случайных погрешностей возможно только на основе теории случайных процессов и математической статистики.
Математически случайную погрешность, как правило, можно представить белым шумом: как непрерывную случайную величину, симметричную относительно 0, независимо реализующуюся в каждом измерении (некоррелированную по времени).
Основным свойством случайной погрешности является возможность уменьшения искажения искомой величины путем усреднения данных. Уточнение оценки искомой величины при увеличении количества измерений (повторных экспериментов) означает, что среднее случайной погрешности при увеличении объёма данных стремится к 0 (закон больших чисел).
Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельности слабо влияет на результат измерения. По этой причине часто полагают распределение случайной погрешности «нормальным» (см. Центральная предельная теорема). «Нормальность» позволяет использовать в обработке данных весь арсенал математической статистики.
Однако априорная убежденность в «нормальности» на основании ЦПТ не согласуется с практикой — законы распределения ошибок измерений весьма разнообразны и, как правило, сильно отличаются от нормального.
Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления).
Систематическая погрешность— погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.
Систематическую ошибку нельзя устранить повторными измерениями. Её устраняют либо с помощью поправок, либо «улучшением» эксперимента.
Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).
Надо отметить, что деление погрешностей на случайные и систематические достаточно условно. Например, ошибка округления при определённых условиях может носить характер как случайной, так и систематической ошибки.
По способу измерения
Погрешность прямых измерений вычисляется по формуле
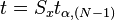
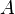
Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины. Если 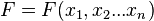
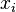
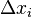
Погрешность косвенных невоспроизводимых измерений вычисляется аналогично вышеизложенной формуле, но вместо