Что называется сочетанием размещением перестановкой
Сочетания. Размещения. Перестановки
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Где 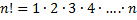
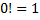
Рассмотрим пример: сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
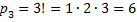
Или такой пример. Порядок выступления семи участников на студенческой конференции определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение: каждый вариант жеребьевки отличается только порядком участников, то есть является перестановкой из 7 элементов. Их число находится
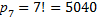
Пример. К кассе за получением денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?
Решение: очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырех человек, их число равно
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо их порядком, либо составом элементов.
Число всех возможных размещений рассчитывается
Пример: сколько можно составить сигналов из 6 флажков различного цвета, взятых по два?
Пример: расписание одного дня состоит из пяти уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Решение: каждый вариант расписания представляет набор 5 дисциплин из 11, отличающийся от других вариантов, как составом дисциплин, так и порядком их следования, то есть является размещением из 11 элементов по 5. Число вариантов расписания находят по формуле
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
Пример: сколькими способами можно выбрать 2 детали из ящика, содержащего 10 деталей?
Пример: в шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение: каждая партия играется двумя участниками из 16 и отличается только составом пар участников, то есть представляет собой сочетание из 16 элементов по два
Пример: имеется 6 штаммов бактерий. Для определения скорости их роста необходимо выбрать три штамма. Сколькими способами можно это сделать?
Решение: способы отбора считаются различными, если каждый отобранный штамм различается хотя бы одним элементом. Это число
То есть имеется 20 способов.
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
При решении задач комбинаторики используют следующие правила.
Правило суммы: если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно 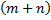
Правило произведения: если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А,В) в указанном порядке может быть выбрана 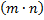
Пример: в студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение: по правилу умножения двух девушек можно выбрать 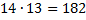
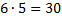
Контрольные вопросы
1. Что называют графом?
2. Какие вершины графа можно назвать смежными?
3. Возможно ли начертить граф с нечетным числом нечетных вершин?
4. Чем определяется полный граф?
5. Что называют перестановками, размещениями, сочетаниями?
6. Сформулировать правила суммы и произведения.
Мастер-класс по теме «Элементы комбинаторики: перестановки, сочетания и размещения»
Разделы: Математика
Элементы комбинаторики: перестановки, сочетания, размещения.
“Число, положение и комбинация – три
взаимно пересекающиеся, но различные
сферы мысли, к которым можно
отнести все математические идеи”.
Джозеф Сильвестр (1844 г.)
Оборудование: компьютеры, проектор, экран, презентация, электронные и на бумажных носителях тесты, задачи “Судоку”, кубики Рубика, папки для ВСР (внеаудиторная самостоятельная работа), рабочие тетради, чистые ватманы, калькуляторы, цветная бумага, клей, ножницы, фломастеры.
I. Организационный момент
Сообщение целей и задач занятия: В связи с тем, что по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа, а рассмотреть нужно много материала, решать задачи, создать проект, вам было выдано задание на внеаудиторную самостоятельную работу следующее: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2. Презентация
В календарно-тематическом плане по дисциплине “Математика” на 2 курсе специальности “Технология деревообработки” на тему “Основные понятия комбинаторика: перестановки, размещения, сочетания” отводится 2 часа. Изучить теоретический материал, решить задачи разных видов за такой временной промежуток невозможно. Для достижения глубокого изучения материала было выдано задание на внеаудиторную самостоятельную работу: в литературе по истории математики, в энциклопедиях, в учебниках и в интернете найти материал о разделе математики, имеющем звучное название “комбинаторика”. Слайды № 1–2.
Запись даты, темы урока.
II. Работа над темой занятия
Из глубокой древности до современного человечества дошли сведения о том, что уже тогда люди занимались выбором объектов и расположения их в том или ином порядке и увлекались составлением различных комбинаций. Так, например, в Древнем Китае увлекались составлением квадратов, в которых заданные числа располагали так, что их сумма по всем горизонталям, вертикалям и главным диагоналям была одной и той же (современная игра – задача “Судоку”). Такие задачи вы могли встречать в журналах и газетах. В частности, наша Мариинская газета “Вперед” довольно часто предлагает читателям такие задачи. В Древней Греции подобные задачи возникали в связи c такими играми, как шашки, шахматы, домино, карты и т.д.
Комбинаторика – самостоятельная ветвь математической науки. Cлайд № 3
Как трактует это слово Большой Энциклопедический Словарь?
Комбинаторика – это раздел математики, в котором изучаются простейшие “соединения”: перестановки, размещения, сочетания. Этот раздел иначе называют “комбинаторный анализ”.
Сегодня мы будем рассматривать перестановки, размещения, сочетания, как соединения, как комбинаторные конфигурации.
Разделы комбинаторики: перечислительная, структурная, вероятностная, топологическая – слайд № 5.
Давайте вспомним известное вам из детства сказание о том, как богатырь или другой добрый молодец, доехав до развилки трех дорог, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый КОМБИНАТОРИКОЙ, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую – слайд № 6.
Итак, комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.
Перестановки-соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их

Число n при этом называется порядком перестановки – слайд № 7–10.
Необходимо знать, что 0!=1
Термин “перестановки” употребил впервые Якоб Бернулли в книге “Искусство предположений”.
Примеры решения задач:
Задача №1. Сколькими способами 7 книг разных авторов можно расставить на полке в один ряд?
Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок обозначается Рп и оно равно п!, т.е. Рп = п!, где п! = 1 * 2 * 3 * … п.
Решение: Р7 = 7!, где 7! = 1 * 2 * 3 * 4 * 5 * 6 * 7 =5040, значит существует 5040 способов осуществить расстановку книг.
Ответ: 5040 способов.
Задача № 2 (о квартете)
В знаменитой басне Крылова “Квартет” “Проказница мартышка, Осел, Козел да косолапый Мишка” исследовали влияние взаимного расположения музыкантов на качество исполнения.
Зададим вопрос: Сколько существует способов, чтобы рассадить четырех музыкантов?
Размещения – соединения, содержащие по m предметов из числа n данных, различающихся либо порядком предметов, либо самими предметами; число их.
В комбинаторике размещением называется расположение “предметов” на некоторых “местах” при условии, что каждое место занято в точности одним предметом и все предметы различны.
В отличие от сочетаний размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов <1,2,3>(то есть, совпадают как сочетания).
Термин “Размещение” употребил впервые Якоб Бернулли в книге “Искусство предположений”.
Примеры решения задач:
Задача № 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений.
Размещаются здесь десять цифр по 6. Значит, ответ на выше поставленную задачу будет:
Задача № 2. В группе ТД – 21 обучается 24 студентов. Сколькими способами можно составить график дежурства по техникуму, если группа дежурных состоит из трех студентов?
Ответ: 12144 способа
Сочетания-соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом; число их 
Таким образом, количество вариантов при сочетании будет меньше количества размещений. Cлайды № 14–16.
В комбинаторике сочетанием из n по m называется набор m элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Термин “сочетание” впервые встречается у Блеза Паскаля в 1665 году.
Примеры решения задач:
Задача №1. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?
Решение: Так как кнопки нажимаются одновременно, то выбор этих кнопок – сочетание. Отсюда возможно
Ответ: 120 вариантов.
Задача № 2. Сколько экзаменационных комиссий, состоящих из 3 членов, можно образовать из 10 преподавателей?
Решение: По формуле находим:

Ответ: 120 комиссий.
Библиографическая справка – слайд № 17.
Общее у всех этих задач то, что их решением занимается отдельная область математики, называемая комбинаторикой. “Особая примета” комбинаторных задач – вопрос, который всегда можно сформулировать так, чтобы он начинался словами: “Сколькими способами…?”. Cлайд № 18.
3. Решение задач: тексты задач с решениями в приложении 1 – начало на слайде № 19.
4. Исторические сведения о комбинаторике на слайдах № 20–21 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).
5. Связи комбинаторики на слайдах № 22–31 (частично даны сведения при изучении темы, остальные данные для проекта студенты возьмут из материалов для ВСР).
6. Выдвижение гипотезы. Гипотеза – это научное предположение, выдвигаемое для объяснения каких-нибудь явлений, вообще – предположение, требующее подтверждения.
8. Защита проектов: при защите проекта сделать вывод: подтверждает ли проект выдвинутую гипотезу или опровергает.
9. Тестирование: Часть студентов тестируется на компьютерах, остальные – на бумажных носителях по теме занятия. По мере выполнения тестов студенты решают задачу “Судока” или собирают кубик Рубика.
10. При выходе из кабинета каждый студент выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
1. Фадеев Д.К., Никулин М.С., Соколовский. Элементы высшей математики для школьников. Москва. “Наука”, 1987 год.
2. Грэхем Р., Кнут Д.А., Паташник О. Конкретная математика.. Москва “Мир”, 1998 г.
3. Богомолов Н.В. Практические занятия по математике: Учеб. Пособие для техникумов, Москва. “Высшая Школа, 1983.
4. Перельман Я.И. “Занимательная алгебра. Занимательная геометрия, Москва, АСТ “Астрель”, 2002 год.
5. Савин А.П. “Энциклопедический словарь юного математика”, Москва “Педагогика”, 1985.
6. Сканави М.И. “Сборник задач по математике для поступающих в вузы”, Москва, “Высшая школа”, 1998 г.
8. Элементы теории вероятностей. Математика. Приложение к газете «Первое сентября», № 41, 42.
10. Лютикас В.С. Факультативный курс по математике: Теория вероятностей, Москва, “ Просвещение”, 1990.
12. Андреева Е. В. “Комбинаторные задачи”, Москва, “Чистые пруды”, 2005 г.
Лекция по теме «Комбинаторика. Перестановки, размещения и сочетания»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
1.Основные правила комбинаторики
Например: сколько существует способов выбора 3 человек из 20? Сколько существует вариантов составления расписания? Задачи такого типа называются комбинаторными, а раздел математики называется комбинаторикой.
Комбинаторика – это раздел математики, изучающий вопросы о том, сколько комбинаций (соединений) определенного вида можно составить из данных элементов.
Основные правила комбинаторики. 1. Правило умножения (произведения); 2. Правило сложения (суммы).
(чаще всего при решении задач используют правило произведения) Пример 1. Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3?
Решение: в качестве первой цифры может быть выбрана любая из цифр 1, 2, 3 (т. е. три варианта). Второй цифрой может быть выбрана любая из четырех данных цифр 0, 1, 2, 3. Чтобы найти количество всевозможных двузначных чисел надо 3 умножить на 4.
Получится 12 чисел.
Пример 2. Сколько различных трехзначных чисел можно составить с помощью цифр 0, 1, 2, 3?
Решение: На первое место можно поставить любую из цифр 1, 2, 3. ( три варианта). На второе – четыре варианта, на третье место тоже четыре варианта. Значит по правилу произведения 3* 4 * 4 = 48 Ответ: 48 чисел.
Для решения этой задачи использовано правило произведения. Правило произведения. Если существует n вариантов выбора первого элемента и для каждого из них имеется m вариантов выбора второго элемента, то всего существует n*m различных пар с выбранными таким образом первым и вторым элементами.
2.Перестановки, размещения и сочетания
Но мы должны научиться решать задачи, используя формулы:
перестановки, размещения и сочетания.
Сначала дадим определение факториала.
Факториалом натурального числа n называется произведение
всех натуральных чисел от 1 до n
Обозначается n! читается: «эн факториал»
n! = 1 

Примеры. 1! = 1; 5! = 1*2*3*4*5 = 120; 0! = 1
Определение: комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.
Обозначение: Рn
Формула: Рn = n! где п – число элементов входящих в перестановку.
Пример1. В турнире участвует 6 команд. Сколько вариантов распределения очередности участия между ними возможно? Решение: Р6 = 6! = 1*2*3*4*5*6 = 720
Ответ: 720 вариантов
Пример 2. Сколько различных трехзначных чисел можно составить из цифр 3, 4, 5. Если цифры не повторяются?
Решение: мы имеем только три цифры и при составлении чисел мы эти цифры просто переставляем (т. е меняем местами). Применим формулу Р3 = 3! = 1*2*3 = 6
Пример 3. Найти значение выражения:



Определение. Размещениями из n элементов по m элементов (n 
элементов, взятых из данных n разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Обозначение: Аn Формула: Аn m  , где n
, где n  m
m
Пример 1. Сколькими способами можно обозначить данный вектор, используя буквы А, Б, В, С, Д, Е?
Решение: по условию задачи даны 6 букв. Для обозначения вектора используются 2 буквы, причем порядок этих букв в обозначении имеет значение. Поэтому задача сводится к нахождению числа размещений
из 6 по 2. Находим А
Пример 2. На третьем курсе 9 предметов. Сколькими способами можно составить расписание на один день, если в учебный день разрешается проводить занятия только по 4 разным предметам?
Решение: всего 9 предметов, разрешается проводить только 4 предмета,
причем предметы разные. А
Ответ: 3024 способа
Пример 3 . Сколько можно записать трехзначных чисел, используя все 9 цифр ( кроме 0)?
Решение: всего цифр 6, одновременно берем 3 цифры, причем порядок
цифр имеет значение. А
Определение. Комбинации из n элементов по m элементам, которые отличаются друг от друга хотя бы одним элементом, называются сочетаниями.
Обозначение : Сn m Формула: Cn m  , где n
, где n  m
m
Пример 1. Сколькими способами можно распределить 3 путевки в один санаторий между пятью желающими?
Решение: Всего желающих 5 человек, путевок 3, порядок не важен т.к.
все путевки в один и тот же санаторий. Значит это сочетание.
сочетания С
Пример 3. В цехе работают 12 человек: 5 женщин и 7 мужчин. Сколькими способами можно сформировать бригаду из 7 человек, что бы в ней было 3 женщины?
Решение: сначала найдем количество выбора женщин. Всего женщин 5, в бригаде должно быть 3 женщины.
С 
Найдем количество выбора мужчин. Всего мужчин 7, в бригаде должно быть 4 мужчины.
С 
И применим правило произведения:
С5 3 

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
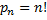
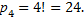
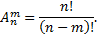

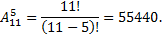

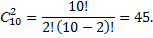

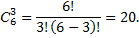
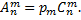







 , где n
, где n  m
m


 , где n
, где n  m
m