Что называется событием в математике
Лекция «События.Виды событий.Комбинации событий!
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Все, что происходит или не происходит в реальной действительности, называют явлениями или событиями. Если некоторое событие происходит довольно часто, то в его наступлении существует определенная закономерность. Раздел математики, изучающий закономерности массовых явлений называется теорией вероятностей.
1) Событие, которое в некотором испытании может произойти, а может и не произойти, называют случайным событием.
2) Событие, которое в данном испытании обязательно произойдет, называют достоверным событием.
3) Событие, которое в данном испытании наступить не может, называют невозможным событием.
Играющий бросает кубик и смотрит, какое число выпало на грани, которая располагается сверху. Какие предположения он может сделать, когда бросает игральный кубик? Например, такие:
Ø событие А – выпадет цифра 1, 2, 3, 4, 5 или 6 – достоверное;
Ø событие В – выпадет цифра 7, 8 или 9 – невозможное;
Ø событие С – выпадет цифра 1 – случайное.
4) События несовместны, если появление одного из них исключает появление другого.
Два события, которые в данных условиях могут происходить одновременно, называют совместными, а те, которые не могут происходить одновременно, – несовместимыми.
5) События называются равновозможными, когда в их испытании нет преимуществ.
Среди данных событий указать пары, которые являются совместными, а какие – несовместимыми.
1. Таня и Ваня сыграли партию в шахматы:
а) Таня выиграла; Ваня проиграл; б) Таня проиграла; Ваня проиграл.
2. Брошен игральный кубик. На верхней грани оказалось:
а) число 6; число 5; б) число 6; четное число.
Суммой (объединением 
Произведением (пересечением 
Например. Пусть в опыте с бросанием игральной кости события: А – выпало число очков, кратное 2; В – выпало число очков, кратное 3. Тогда событие А + В означает, что выпало хотя бы одно из чисел 2, 3, 4, 6; событие АВ – выпало число 6.
Задача . Пусть из колоды вынимают одну карту. Рассмотрим события:
А – это король, В – это карта масти пик.
Тогда: А + В – вынут король или карта масти пик;
АВ – из колоды вынут король пик.
Для каждого события А можно рассмотреть противоположное событие Ā, которое наступит тогда и только тогда, когда событие А не наступает.
Например: А – выпадение чётного числа очков, Ā – выпадение нечетного числа очков; А – попадание в цель, Ā – промах.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Понятие вероятности события
Вы будете перенаправлены на Автор24
Основными понятиями теории вероятностей являются понятия события и вероятности события.
Событие
Событием будем называть любое утверждение, которое может как произойти, так и не произойти.
Обычно события обозначаются большими английскими буквами.
В связи с тем, что событие может иметь две вариации исхода («произошло» и «не произошло») мы сталкиваемся с понятие вероятности такого события.
Понятие вероятности события
Вероятностью события будем называть число, которое обозначает степень возможности, что такое событие произойдет.
Чтобы определить границы значения этого числа введем понятие достоверного и невозможного событий.
Достоверным событием будем называть такое, которое произойдет при любых обстоятельствах.
Вероятность такого события мы будем принимать за единицу.
Невозможным событием будем называть такое, которое не может произойти ни при каком обстоятельстве.
В современной теории вероятности принято выделять четыре определения для вероятности: классической, геометрическое, статистическое и аксиоматическое определения. Рассмотрим их отдельно.
Готовые работы на аналогичную тему
Классическое определение
Классическое определение связано с такими неопределяемыми понятиями как равновозможность и элементарность события. Интуитивно их можно понять на следующих примерах:
Равновозможность: При подбрасывании монеты она может упасть как аверсом, так и реверсом независимо от внешних условий. То есть можно сказать что вероятность выпадения одной или другой стороны по сути одинакова.
Математически это выглядит следующим образом:
Геометрическое определение
Статистическое (частотное) определение
Аксиоматическое определение
Данное определение задается с помощью аксиоматики Колмогорова.
Примеры задач
Решение.
Тут мы будем использовать геометрическое определение. Изобразим вначале область, в которую в принципе может попасть эта точка (рис. 1).
Из этого рисунка видим, что
$S=8\cdot 5=40,s=3\cdot 3=9$
Тогда из геометрического определения:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 17 06 2021
События, виды событий
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба <Г>и выпадение цифры <Ц>при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = <1, 2, 3, 4, 5, 6>.
Элементарные события, составляющие пространство Ω, обозначаются ω1, ω2, …, ω6.
Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
2. Определим еще несколько важных понятий теории вероятностей
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω=
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Примеры и разбор решения заданий тренировочного модуля
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
События. Виды событий



Одно из базовых понятий – это событие. События бывают достоверными, невозможными и случайными.
Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания. Пример невозможного события: в условиях земного тяготения подброшенная монета улетит вверх.
И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила/направление броска, сопротивление воздуха и т.д.
Подчёркнутый критерий случайности очень важен – так, например, карточный шулер может очень ловко имитировать случайность и давать выигрывать жертве, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.
Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.
События (любые) обозначают большими латинскими буквами 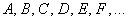
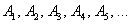
Исключение составляет буква 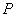
Запишем следующие случайные события:
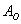
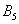
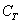
Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).
Следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле снова показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие 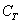
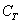
Другая важная характеристика событий – это их равновозможность. Два или большее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другие. Например:
· выпадение орла или решки при броске монеты;
выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
извлечение карты трефовой, пиковой, бубновой или червовой масти из колоды.
При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.
Могут ли быть те же события не равновозможными? Могут! Например, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Как говорится, ещё одна лазейка для мошенников. События 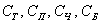
Тем не менее, в рассмотренных трёх случаях при потере равновозможности всё же сохраняется случайность событий.
Совместные и несовместные события. Противоположные события.
Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой вверху. Например:
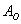
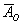
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
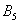
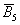
Либо пять, либо не пять – третьего не дано, т.е. события несовместны и противоположны.
Аналогично – или трефа или карта другой масти:
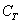
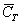
Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу. Однако в различных задачах с одним и тем же объектом могут фигурировать разные события, например, для игрального кубика характерно рассмотрение следующего набора:
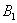
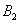
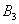
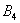
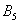
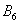
События 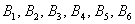
Ещё одно важное понятие, которое нам скоро потребуется – это элементарность исхода (события). Если совсем просто, то элементарное событие «нельзя разложить на другие события». Например, события 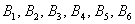
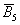
В примере с картами события 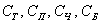
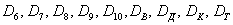
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и, разумеется, 36 несовместных элементарных исходов тоже образуют полную группу событий.
Совместные события менее значимы с точки зрения решения практических задач, но обходить их стороной не будем. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого.
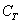
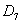
Если быть совсем лаконичным, одно не исключает другого.
Понятие совместности охватывает и большее количество событий:
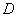
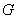
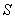
Ситуация, конечно, довольно редкая, но совместное появление всех трёх событий в принципе не исключено. Следует отметить, что перечисленные события совместны и попарно, т.е. может быть только ливень с грозой или грибной дождик, или погромыхает неподалёку на фоне ясного неба.
Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:
Операция сложения событийозначает логическую связку ИЛИ,
а операция умножения событий – логическую связку И.
1) Суммой двух событий 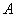
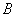
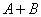
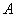
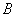
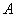
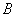
Правило распространяется и на большее количество слагаемых, например, событие 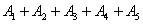
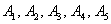
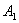
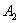
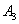
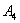
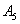
События 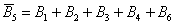
Событие 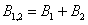
Событие 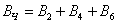
Событие 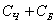
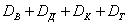
Чуть занятнее дело с совместными событиями:
Событие 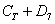
Событие 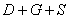
– или будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.
То есть, событие 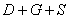
2) Произведением двух событий 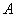
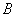
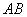
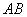
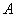
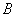
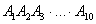
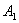
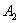
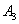
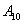
Рассмотрим испытание, в котором подбрасываются две монетыи следующие события:
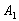
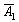
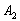
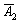
Тогда:
– событие 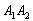
– событие 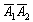
– событие 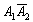
– событие 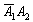
Нетрудно заметить, что события 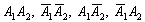
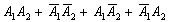
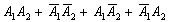
Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае – две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:
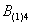
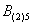
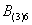
Тогда событие 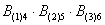
…Понимаю, что, возможно, разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько анонимов, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали.










