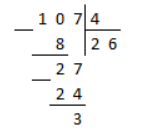Что называется смешанной дробью
Смешанные дроби
Что такое смешанная дробь
Число, содержащее в себе целую и дробную части, называется смешанной дробью.
По сути, данное понятие представляет собой сумму целого числа и правильной дроби:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Превращение смешанной дроби в неправильную
Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.
Преобразование смешанной дроби в неправильную можно записать в виде формулы:
Выполнение действий со смешанными дробями, формулы и примеры
Сложение
Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.
Формульное выражение сложения смешанных чисел:
\(a\frac bc+d\frac ef=\left(a+d\right)+\left(\frac bc+\frac ef\right)\)
Вычисляем наименьший общий знаменатель дробных слагаемых:
Вычитание
Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.
Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:
\(a\frac bc-d\frac ef=\left(a+\frac bc\right)-\left(d+\frac ef\right)\;=\left(a-d\right)+\left(\frac bc-\frac ef\right)\)
В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:
\(a\frac bc-d\frac ef=\left(\left(a-d\right)-\frac ef\right)+\frac bc\)
Для решения этого выражения найдем наименьший общий знаменатель:
8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.
Умножение и деление
Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.
Формула умножения смешанных чисел выглядит так:
Формула деления смешанных дробей:
При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.
Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.
Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.
Смешанные дроби
Вы будете перенаправлены на Автор24
Определение смешанной дроби
Перевод смешанного числа в неправильную дробь
Алгоритм перевода смешанного числа в неправильную дробь:
Готовые работы на аналогичную тему
Решение.
Воспользуемся алгоритмом перевода смешанного числа в неправильную дробь.
Запишем краткую запись данного решения:
Решение.
Выделение целой части из неправильной дроби
При получении числового решения не принято оставлять ответ в виде неправильной дроби. Неправильная дробь преобразуется в равное ей натуральное число (если числитель делится нацело на знаменатель), или выделяют целую часть из неправильной дроби (если числитель не делится нацело на знаменатель).
Выделением целой части из неправильной дроби называется замена дроби равным ей смешанным числом.
Решение.
Выполним деление в столбик:
Сложение смешанного числа и натурального числа
Правило сложения смешанного и натурального числа:
Для сложения смешанного и натурального числа нужно к целой части смешанного числа прибавить данное натуральное число, дробная часть остается без изменения:
Решение.
Сложение двух смешанных чисел
При сложении двух смешанных чисел складываются их целые части и дробные части.
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 21 06 2021
Смешанные дроби или смешанные числа.
Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.
Как сделать из неправильной дроби правильную дробь?
Рассмотрим неправильную дробь \(\frac<21><9>\)
Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.

Получаем дробь \(2\frac<3><9>\), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а \(\frac<3><9>\) – правильная дробь.
Смешанные дроби состоят из целой и дробной части.
Рассмотрим еще одну неправильную дробь \(\frac<76><5>\)
Разделим ее столбиком:

Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: \(\frac<508><17>\)
Решение:
Разделим дробь столбиком:
Ответ: Получили смешанную дробь \(29\frac<15><17>\)
Пример №2:
Представьте число в виде неправильной дроби: а) \(9\frac<2><3>\), б) \(1\frac<3><7>\)
Решение:
а) \(9\frac<2> <3>= \frac<9 \times 3 +2> <3>= \frac<29><3>\\\\\)
б) \(1\frac<3> <7>= \frac<1 \times 7 +3> <7>= \frac<10><7>\\\\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил \(\frac<2><5>\) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь \(\frac<2><5>\), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
\(120 \div 5 = 24\) задачи это одна часть или \(\frac<1><5>\)
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
\(24 \times 2 = 48\) задач
Ответ: за неделю Миша решил 48 задач.
Что такое смешанная дробь с примером?
еще, что такое неправильная дробь с примером?
Далее, Какова формула смешанной фракции?
Формула смешанной фракции
Тогда что вы подразумеваете под смешанной дробью?
Более конкретно, смешанная фракция просто неправильная дробь, записанная как сумма целого числа и правильной дроби. Например, неправильная дробь 3/2 может быть записана как эквивалентная смешанная дробь 1-1 / 2 (читается вслух как «полторы» или «полторы»).
Что такое правильный пример дроби?
Что такое неправильная дробь, приведите два примера?
Дробь, в которой числитель (верхнее число) больше или равен знаменателю (нижнему числу). Так что обычно это «тяжеловесно». Пример: 5/3 (пять третей) и 9/8 (девять восьмых) неправильные дроби.
Как решить неправильную дробь?
Чтобы преобразовать смешанную дробь в неправильную, выполните следующие действия:
Как записать 17 4 как смешанное число?
Ответ: 17/4 как смешанное число 4 ¼.
Какая дробь равна 8 5 9?
8 5/9 как неделимая дробь.
Какой пример смешанного числа?
Какие бывают виды дроби?
Какие бывают три типа дробей? Три типа дробей, основанные на числителе и знаменателе: правильные, неправильные и смешанные фракции.
Каковы 2 примера правильной дроби?
Какие бывают 7 типов фракций?
Типы дробей с примером: сколько типов дробей существует?
| Что такое 7 типов дробей?
Какие бывают примеры двух дробей?
Дробь называется правильной дробью, если числитель меньше знаменателя. Примеры: ⅓, ⅔, ⅖, 3/7, 5/9, И т.д.
Смешанная фракция?
Более конкретно, смешанная фракция просто неправильная дробь, записанная как сумма целого числа и правильной дроби. Например, неправильная дробь 3/2 может быть записана как эквивалентная смешанная дробь 1-1 / 2 (читается вслух как «полторы» или «полторы»).
Что такое 1 и 2/3 как неправильная дробь?
Что такое 7/4 как смешанное число?
Ответ: 7/4 как смешанное число можно записать как 1 3/4.
Что такое 5/2 в смешанном числе?
Что 9 4 в смешанном числе?
Ответ: 9/4 как смешанное число 2 1/4.
Что такое 11 3 как смешанное число?
Что 19 3 как смешанное число?
Что такое 29 3 как смешанное число?
29/3 как смешанное число 9 2/3.
Какой вид дроби равен 5 9?
Таблица преобразования десятичных и дробных чисел
| Доля | Эквивалентные дроби | |
|---|---|---|
| 2/9 | 4/18 | 18/81 |
| 4/9 | 8/18 | 36/81 |
| 5/9 | 10/18 | 45/81 |
| 7/9 | 14/18 | 63/81 |
Какие бывают 8 типов фракций?
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо: