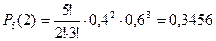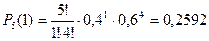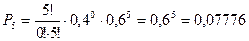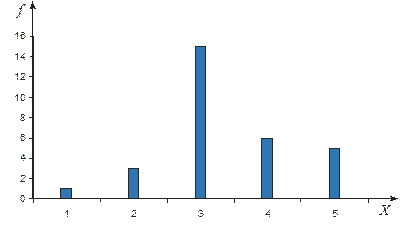Что называется случайной величиной дискретной и непрерывной случайной величиной
Лекция № 4. Дискретные и непрерывные случайные величины



При проведении стохастического эксперимента формируется пространство элементарных событий – возможных исходов этого эксперимента. Считают, что на этом пространстве элементарных событий задана случайная величина X, если задан закон (правило) по которому каждому элементарному событию сопоставляется число. Таким образом, случайную величину X можно рассматривать, как функцию, заданную на пространстве элементарных событий.
? Дискретная случайная величина – случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.
? Непрерывная случайная величина – случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины – бесконечно.
? Закон распределения случайной величины – соответствие между возможными значениями случайной величины и их вероятностями, т.е. каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение. Закон распределения случайной величины может быть задан таблично (в форме таблицы), аналитически (в виде формулы) и графически.
| X | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
В результате испытания дискретная случайная величина X принимает одно и только одно из возможных значений, поэтому события X=x1, X=x2, …, X=xn образуют полную группу попарно несовместных событий, и, значит, сумма вероятностей этих событий равна единице, т.е. p1 + p2 +… + pn =1.
Пример 2.23. Студент сдает два экзамена: по математике и информатике. Составьте закон распределения случайной величины X, числа полученных пятерок, если вероятность получения пятерки по математике равна 0,7, а по информатике – 0,6.
Решение. Пусть A1 и A2 – события, заключающиеся в том, что математика и информатика сданы на «5». Возможные значения X есть 0, 1, 2, причем
Следовательно, закон распределения данной случайной величины в форме таблицы и в виде графика будет таким (см. рис. 2.4).
Контроль: 0,12 + 0,46 + 0,42 = 1.
 |
? Функция распределения случайной величины – функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение, меньшее x, т.е.
Контроль: 0,001+ 0,01+ 0,044 + 0,117+ 0,205 + 0,246 + 0,205 + 0,117 + 0,044 + + 0,01 + 0,001 = 1.
Дискретные и непрерывные случайные величины
Рассматривая случайные события, сталкивались с такими, которые состоят в появлении того или иного числа. Например, при бросании игрального кубика выпавшие очки выражаются числом от 1 до 6. Наперед определить какое именно число появится в результате опыта невозможно. В этом смысле число выпавших очков при бросании кубика есть величина случайная (СВ). Случайная величина является количественной характеристикой случайного результата опыта.
Определение. Случайной величинойназывается величина, которая в результате опыта может принимать то или иное числовое значение, причем заранее неизвестно какое именно.
· случайные величины заглавными буквами латинского алфавита: X, Y, Z, U, V …
· значения случайных величин малыми буквами с индексами: x1, x2,…y1, y2,…
Примеры случайных величин:
1) X – число попаданий в мишень при двух выстрелах;
возможные значения этой СВ: x1 = 0 (нет ни одного попадания), x2 = 1 (одно попадание), x3 = 2 (два попадания).
2) Y – рост случайно выбранного человека;
Возможные значения СВ Y перечислить нельзя, можно лишь указать промежуток, которому эти значения принадлежат: ymin – ymax.
Примеры 1) и 2) показывают, что случайные величины можно разделить на две категории: те, которые принимают отдельные, изолированные значения на числовой прямой и те, которые заполняют некоторый промежуток на числовой прямой. Эти категории образуют Дискретные и Непрерывные случайные величины.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать счетное, хотя и бесконечное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
§2. Закон распределения дискретной случайной величины.
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
Найдем вероятности пяти попаданий из пяти возможных, четырех из пяти, трех из пяти, двух из пяти, одного из пяти и нуля из пяти по формуле Бернулли:
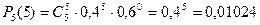
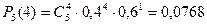
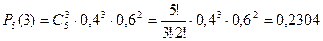
Проверим, что сумма вероятностей равна единице:
Запишем ряд (таблицу) распределения СВ:
| X | ||||||
| p | 0,07776 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,01024 |
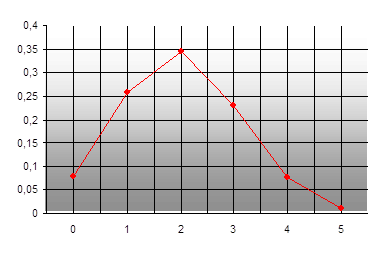 |
Представим графически зависимость числа попаданий от их вероятностей.
При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.
§3. Функция распределения случайной величины.
Задание случайной величины путем определения значений этой величины и вероятностей этих значений применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. P(Х 5, то меньше такого х все шесть значений: вероятность того, что X
Дата добавления: 2016-05-25 ; просмотров: 3970 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Что называется случайной величиной дискретной и непрерывной случайной величиной
1. Формирование представление о случайной величине, дискретных и непрерывных случайных величинах.
2. Знакомство с законом распределения дискретной случайной величины, функцией распределения и плотностью распределения непрерывной случайной величины, числовых характеристиках случайных величин.
1. Виды случайных величин.
2. Закон распределения дискретной случайной величины.
3. Функция распределения вероятностей случайной величины.
4. Плотность распределения вероятностей непрерывной случайной величины.
5. Математическое ожидание.
6. Дисперсия и среднеквадратическое отклонение.
1. Виды случайных величин.
Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений.
По множеству возможных значений различают дискретные и непрерывные случайные величины.
Дискретными называются случайные величины, значениями которых являются только отдельные точки числовой оси. (Число их может быть как конечно, так и бесконечно).
Пример: Число родившихся девочек среди ста новорожденных за последний месяц- это дискретная случайная величина, которая может принимать значения 1,2,3,…
Непрерывными называются случайные величины, которые могут принимать все значения из некоторого числового промежутка.
2. Закон распределения дискретной случайной величины.
Закон распределения дискретной случайной величины— это соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения можно задать таблично, аналитически, графически.
При задании закона распределения таблично, в первую строку таблицы вносятся возможные значения случайно величины, а во вторую- их вероятности.
Пример: Монету подбросили 3 раза. Запишите закон распределения числа выпадения «герба».
Возможные значения данной случайной величины: 0, 1, 2, 3.
Найдем вероятность того, что «герб» не появится (0 раз).
Найдем вероятность того, что «герб» появится 1 раз.
Найдем вероятность того, что «герб» появится 2 раза.
Найдем вероятность того, что «герб» появится 3 раза.
Тогда закон распределения данной дискретной случайной величины можно представить таблицей:
Для наглядности закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки с координатами (xi ; pi), а затем соединяют их отрезками прямых. Полученная фигура называется многоугольником распределения.
Однако, такой способ задания (перечисление всех возможных значений случайной величины и их вероятностей) не подходит для непрерывных случайных величин. Составить перечень их возможных значений невозможно.
3. Функция распределения вероятностей случайной величины.
Дадим новый способ задания любых типов случайных величин. С этой целью введем функцию распределения вероятностей случайной величины.
Функцией распределения случайной величины называют функцию F ( x ), определяющую вероятность того, что случайная величина Х в результате испытания примет значение меньшее х, т.е. F ( x ) P ( X x ).
Геометрически это равенство можно истолковать так: F ( x ) –есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Иногда вместо термина «функция распределения» используется термин «интегральная функция».
Свойства функции распределения:
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале (а; b ), равна приращению функции распределения на этом интервале:
Пример: Случайная величина Х задана функцией распределения:
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0; 2).
Следствие: Если возможные значения непрерывной случайной величины распределены на всей числовой оси, то справедливы следующие предельные соотношения:
Рассмотренные выше свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у=0, у=1 (1 свойство).
4. При возрастании значения х в интервале ( a ; b ), в котором заключены все возможные значения случайной величины, график растет вверх (2 свойство).
5. При ординаты графика равны 0, при ординаты графика равны 1 (3 свойство).
Замечание: График функции распределения дискретной случайной величины имеет ступенчатый вид.
Пример: Дискретная случайная величина Х задана таблицей распределения:
Найдите функцию распределения и постройте ее график.
Итак, функция распределения имеет следующий вид:
4. Плотность распределения вероятностей непрерывной случайной величины.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (дифференциальной функцией).
Плотность распределения вероятностей непрерывной случайной величины Х называют функцию f ( x )- первую производную от функции распределения F ( x ).
Пример: Задана плотность вероятностей случайной величины Х.
Найдите вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Свойства плотности распределения вероятностей:
Свойство 1: Плотность распределения- неотрицательная функция: f ( x ) > 0.
Часто, для того чтобы характеризовать случайную величину используют числа, которые описывают случайную величину суммарно. Такие числа называются числовыми характеристиками случайной величины. К числу важнейших числовых характеристик относятся математическое ожидание и дисперсия.
5. Математическое ожидание.
Математическое ожидание приближенно равно среднему значению случайной величины. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и следовательно стреляет лучше.
Пример: Найдите математическое ожидание, зная закон распределения дискретной случайной величины.
Дискретные и непрерывные случайные величины



Как правило, при изготовлении продукции на процесс её производства оказывает влияние множество различных факторов, в результате чего наблюдается разброс значений показателей качества продукцию. Таким образом, показатели качества изготовляемой продукции или оказываемых услуг следует рассматривать как случайные величины.
Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные значения и не могут принимать значения промежуточные между ними. Например, количество негодных деталей в партии может быть только целым положительным числом 1, 2, 3 и т.д., но не может быть 1,3; 1,7 и т.п.
Непрерывной случайной величиной называется такая величина, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.
Например, действительные размеры деталей, обработанных на станке, являются случайными величинами непрерывного типа, так как они могут принять любое численное значение в определенных границах.
Возможности случайных величин принимать при испытаниях те или иные численные значения оцениваются при помощи вероятностей.
Совокупность значений случайных величин, расположенных в возрастающем порядке с указанием их вероятностей для каждого из значений, называется распределением случайных величин (согласно СТБ ГОСТ Р 50779.10 распределение – это функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений).
Распределение случайной величины можно представить в табличном, графическом виде и при помощи статистических оценок.
При представлении распределения случайной величины в табличном виде каждому номеру исследуемой единицы продукции (номеру измерения) соответствует значение показателя качества для данной единицы продукции (результат измерения).
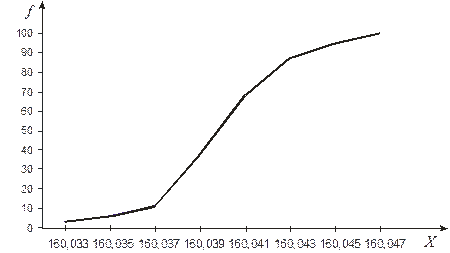
При представлении распределения случайной величины в графическом виде строят график распределения в координатах значение случайной величины – вероятность (частота, частость) значения случайной величины.
На рисунке ниже показаны графики распределения дискретной и непрерывной случайных величин.
Различают теоретические и эмпирические распределения случайных величин. В теоретических распределениях оценка возможных значений случайной величины производится при помощи вероятностей, а в эмпирических — при помощи частот или частостей, полученных в результате испытаний.
Следовательно, эмпирическим распределением случайной величины называется совокупность экспериментальных ее значений, расположенных в порядке возрастания, с указанием частот или частостей для каждого из значений (согласно СТБ ГОСТ Р 50779.10 распределение частот – это эмпирическое отношение между значениями признака и его частотами или его относительными частотами).
Таблица. Пример табличного представления теоретического распределения дискретной случайной величины
| X | X1 | X2 | X3 | X4 | X5 | |
| P(X) | P(X1) | P(X2) | P(X3) | P(X4) | P(X5) | SP(Xi)=1 |
Таблица. Пример табличного представления эмпирического распределения дискретной случайной величины
| X | X1 | X2 | X3 | X4 | X5 | |
| mx | 1/30 | 3/30 | 15/30 | 6/30 | 5/30 | Smxi=1 |
Графически эмпирическое распределение дискретной случайной величины можно представить в виде столбиковой диаграммы, образуемой набором столбцов равной ширины, высоты которых пропорциональны частотам дискретных значений случайной величины.
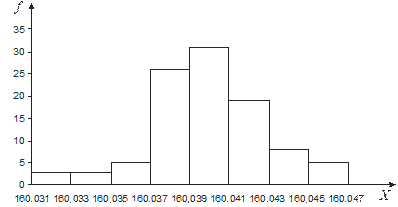
Если случайная величина является непрерывной, то возникают некоторые сложности с представлением ее распределения в виде таблицы или графика. Поэтому на практике при изучении случайных величин непрерывного типа полученные значения разбивают на равные интервалы с таким расчетом, чтобы значение интервала было несколько больше погрешности измерения исследуемой величины. Затем подсчитывают частоты не по действительным значениям случайной величины, а по интервалам. Поэтому таблица эмпирического распределения случайной величины непрерывного типа будет иметь следующий вид.
Таблица. Эмпирическое распределение случайной величины непрерывного типа.
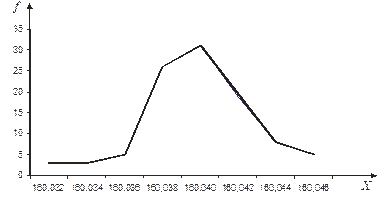
Эмпирическое распределение случайной непрерывной величины графически может быть представлено в виде гистограммы распределения, полигона частот или полигона кумулятивных частот.
Гистограмма распределения представляет собой совокупность соприкасающихся прямоугольников, основания которых равны интервалам разбиения непрерывной случайной величины, а площади пропорциональны частотам, с которыми значения случайной величины попадают в эти интервалы (согласно СТБ ГОСТ Р 50779.10 гистограмма (распределения) – это графическое представление распределения частот для количественного признака, образуемое соприкасающимися прямоугольниками, основаниями которых служат интервалы классов, а площади пропорциональны частотам этих классов).
Полигон частот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны серединам интервалов разбиения, а ординаты – соответствующим частотам.
Полигон кумулятивныхчастот – это ломаная линия, получаемая при соединении точек, абсциссы которых равны верхним границам интервалов разбиения, а ординаты – либо кумулятивным частотам, либо кумулятивным частостям (кумулятивным относительным частотам).
При теоретических описаниях случайных величин непрерывного типа используется функция распределения. Теоретическое распределение случайной непрерывной величины графически может быть представлено в виде интегральной, обратной интегральной, дифференциальной функций распределения и функции интенсивности.
Пусть Х — случайная величина, а х — какое-либо действительное число (при этом Х х1) равна приращению интегральной функции на этом участке, т.е.
Дискретные и непрерывные случайные величины.
По своей физической природе случайные величины могут быть детерминированными и случайными.
Дискретной называют случайную величину, отдельные значения которой можно перенумеровать (число изделий, количество деталей – бракованных и годных и т.п.).
Непрерывной называют случайную величину, возможные значения которой заполняют некоторый промежуток (отклонение размера изготовленной детали от номинала, погрешность измерения, величина отклонения формы детали, высота микронеровностей и т.п.).
Случайная величина не может характеризоваться каким-то одним значением. Для неё необходимо указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.
В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом x > X. Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
Дата добавления: 2016-06-15 ; просмотров: 19415 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ