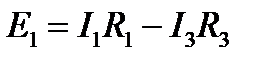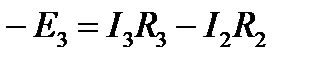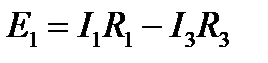Что называется сложной электрической цепью

Сложная электрическая цепь

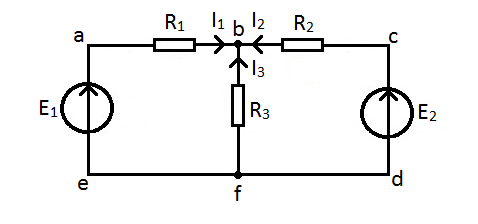
Сложной называется цепь, состоящая из нескольких контуров, и содержащая несколько источников ЭДС. Пример сложной цепи показан на рис. 19. Цепь содержит два источника ЭДС и несколько резисторов. В схеме можно выделить несколько контуров.

Перед началом рассмотрения данной темы необходимо повторить свойства параллельного соединения резисторов.

Рис. 19. Сложная электрическая цепь

Контуром называется любой замкнутый участок электрической цепи. В данной схеме можно выделить три контура: контур a, b, f, e, a, контур b, c, d, f, b и контур: a, c, d, e, а.

Расчет сложных цепей ведется с применением первого и второго законов Кирхгофа. Первый закон Кирхгофа был рассмотрен при изучении параллельного соединения резисторов. Второй закон Кирхгофа гласит: алгебраическая сумма ЭДС, входящих в контур равна алгебраической сумме падения напряжения на элементах этого контура.

Обычно, требуется найти значения токов во всех ветвях, если известны значения ЭДС всех источников и величина всех сопротивлений.

Для решения этой задачи требуется составить и решить систему уравнений. Число уравнений, входящих в систему, равно числу неизвестных токов. Для рассматриваемой схемы потребуется три уравнения, т.к. в схеме три ветви и, соответственно три тока, которые нужно найти.

Расчет сложных цепей производится по определенному алгоритму:

1. Прежде всего, произвольно обозначаем направление токов в ветвях (см. рис. 19). Мы пока не знаем, в какую сторону направлены токи, обозначаем направление токов наугад. Позже, решение задачи укажет нам на ошибку, если она допущена.

2. По первому закону Кирхгофа составляем (n-1) уравнений, где n – число узлов. В нашей схеме два узла: это точки b и f. Для узла b, по первому закону Кирхгофа, запишем: 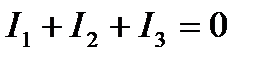, т.к. все три тока направлены к узлу b. (На самом деле такой вариант невозможен. Не может быть, чтобы были токи, подходящие к узлу и не было токов, отходящих от узла. Но сейчас это не имеет значения.)

3. Всего нужно составить 3 уравнения (по числу неизвестных токов). Недостающие уравнения составим по второму закону Кирхгофа для двух любых контуров. Предварительно договоримся, что обход по контуру при составлении уравнения будем совершать по часовой стрелке. Термин обход по контуру следует понимать так: Выбираем на контуре любую точку и начинаем двигаться вдоль контура. «По дороге» записываем встречающиеся на пути ЭДС (Е) и напряжения на резисторах.

ЭДС входит в уравнение с плюсом, если направление стрелки источника совпадает с направлением обхода по контуру. В противном случае запишем его со знаком «минус».

Падение напряжения на сопротивлении (U=I•R) входит в уравнение с плюсом, если направление тока в резисторе совпадает с направлением обхода.

Для контура a, b, f, e, a, запишем:

Для контура b, c, d, f, b:

4) Объединяя составленные нами уравнения, получим систему уравнений:

5) Теперь дело за малым. В систему уравнений нужно подставить известные из условия задачи величины и решить систему относительно токов. Будут получены числовые значения токов.

Если ток получается со знаком «минус», значит, мы неправильно указали его направление и, на самом деле, он протекает в направлении, противоположном, указанному на рис.19.

Чем сложнее схема, тем больше уравнений в системе и тем сложнее ее решить.

Источник

СЛОЖНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА

Общие сведения

Электрические цепи с последовательно-параллельным соеди­нением приемников энергии при питании их от одного источника электрической энергии, а также одноконтурные цепи называют простыми цепями. Расчет этих цепей осуществляется по формулам закона Ома и первого закона Кирхгофа. При этом заданные сопро­тивления часто заменяют одним эквивалентным. Так, цепь на рис. 6.1, а можно привести к элементарному виду с одним экви­валентным сопротивлением г, подключенным к источнику энергии с ЭДС Е₁ (рис. 6.1,6). В данном случае Электрические цепи с несколькими контурами, состоящими из разных ветвей с произвольным размещением потребителей и источников энергии, называются сложными электрическими цепя­ми. Сложные электрические цепи рассчитывают методами: 1) уз­ловых и контурных уравнений; 2) контурных токов; 3) узлового напряжения; 4) наложения (суперпозиции); 5) эквивале­нтного преобразования тре­угольника и звезды сопротив­лений. В первом методе ис- ‘пользуются первый и второй законы Кирхгофа. Первый за­кон был рассмотрен в § 4.3.

Второй закон Кирхгофа

Сложная электрическая цепь(рис. 6.2, а) имеет два узла (Б и Д) и три ветви с токами .Обозначим контуры цепи I — АБДЕА; II — АБВГДЕА; III — БВГДБ. В контуре АБДЕА включены ЭДС Е₁, Е₁ и сопротивления на которых созда­ются падения напряжения: , . Если точку А заземлить, то ее потенциал будет равен нулю. Потенциалы точек Б и Д выразятся следующим образом: ; Если от потенциала от­нять падение напряжения и прибавить к нему ЭДС Е₁, то полу­чим потенциал : , или В левой части полученного равенства оставим ЭДС Е₁ и Е₂, а все остальные его члены перенесем в правую часть. Тогда получим или В левой части этого уравнения записана алгебраическая сумма ЭДС, действующих в первом контуре, а в правой — сумма падений напряжения во всех сопротивлениях, входящих в этот контур. В общем виде для любого контура

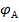
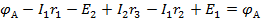
Равенство (6.1) является математическим выражением второго закона Кирхгофа: в любом контуре электрической цепи алгебраиче­ская сумма ЭДС равна алгебраической сумме падений напряжений в отдельных сопротивлениях.

Для каждого контура сложной электрической цепи по второму закону Кирхгофа можно составить

только одно уравнение. При этом особое внимание следует обра­тить на знаки ЭДС и падение напряжения. Вначале произвольно выбирают направление обхода контура. Если действующая в кон­туре ЭДС совпадает с направлением обхода, то ее считают поло­жительной, при обратном направлении ЭДС отрицательна. Паде­ние напряжения на сопротивлении считают положительным, если направление тока в нем совпадает с направлением обхода контура

В электрических цепях встречаются элементы с выводами, на которых имеются напряжения U (сеть напряжения, делитель напряжения и т. д.). В этом случае удобнее использовать следую­щую форму записи второго закона Кирхгофа: . При этом ЭДС напряжения и токи, положительные направления кото­рых совпадают с направлением обхода контура, записываются в соответствующую часть уравнения с положительным знаком. В противном случае эти же величины записываются с отрицатель­ным знаком. Например, для контура (рис. 6.2, б) при обходе его по часовой стрелке имеем

Источник

Электрическая цепь

Электри́ческая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.

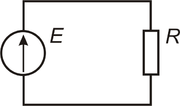
Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

Содержание

Классификация электрических цепей

Неразветвленные и разветвленные электрические цепи

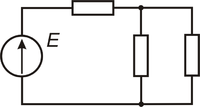
Электрические цепи подразделяют на неразветвленные и разветвленные. На рисунке 1 представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 2. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом

Линейные и нелинейные электрические цепи

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.

Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту от напряжения на этом компоненте называют вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.

Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть прменён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).

Источник

Трудные темы по физике. Сложные электрические цепи

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Аннотация работы

Данная работа представляет из себя модуль дистанционного обучения «Трудные темы по физике. Сложные электрические цепи», разработанный в рамках программы переподготовки управленческих и педагогических кадров «Большие вызовы». Может являться материалом для самостоятельного изучения школьниками, а также вспомогательным материалом для учителей, которые готовят школьников к олимпиадам по физике муниципального и регионального уровней. Представлен как теоретический материал, необходимый для освоения указанной «трудной» темы, так и практический – собрана небольшая коллекция задач из олимпиад прошлых лет с решениями. Распространяется в сети интернет свободно.

1.ПРОГРАММА ДИСТАНЦИОННОГО МОДУЛЯ ОБУЧЕНИЯ «ТРУДНЫЕ ТЕМЫ ПО ФИЗИКЕ. СЛОЖНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ»

Модуль рассчитан на 12 часов, из них 8 часов – разбор методов и решений олимпиадных задач прошлых лет самостоятельно или совместно с наставником, 4 часа – самостоятельное выполнение домашних заданий, обсуждение решений на форуме и обратная связь.

Программа дистанционного модуля обучения «Трудные темы по физике. Сложные электрические цепи»

Тема занятия (теоретическая часть)

Задачи для разбора (практическая часть)

Основные законы электрических цепей. Закон Ома для участка цепи и для полной цепи

Термины и определения. Активное и реактивное сопротивление. Эквивалентная схема.

Классификация олимпиадных задач на электрические цепи

Последовательное и параллельное соединение резисторов, катушек, конденсаторов. Задачи на нахождение полного сопротивление

«простых» цепей. Нахождение эквивалентной схемы.

Метод эквивалентных схем:

Метод соединения узлов

Метод размножения узлов

Метод расщепления ветвей

Задачи «Мост», «Звезда», «Звезда в треугольнике», «Куб», «решетка»

Задачи «Конвертик», «Звезды»

Метод эквивалентных схем:

Задачи на периодические цепи «бесконечная цепь», «челюсти», «вагоны»

Задачи на периодические цепи

Метод Кирхгофа. Алгоритм метода и два правила Кирхгофа.

Метод эквивалентного источника

Задачи на разветвленные цепи с несколькими источниками

Задачи на поиск эквивалентного источника

Задачи на правила Кирхгофа с проверкой решения по балансу мощностей

Любые задачи на электрические цепи, в которых найдены токи во всех ветвях

Метод контурных токов

Задачи по методу Кирхгофа и МКТ

Метод узловых потенциалов

Задачи «перемычка без резистора», «конденсаторы», «нелинейные цепи», «квадратная сетка»

«перемычка с резистором»

Мини-олимпиада по модулю

Соревновательное решение задач по теме модуля.

Изложение трудных для понимания школьниками тем по физике. сложные электрические цепи

Одна из трудных для школьников тем по физике – «Сложные электрические цепи». В разделе представлены материалы, разработанные для дистанционного модуля по этой теме и могут быть использованы как учителями для подготовки детей к соревнованиям по физике, так и для самостоятельного освоения школьниками.

Классификация олимпиадных задач на электрические цепи

Электрические цепи могут включать следующие элементы: источники ЭДС, резисторы, конденсаторы, катушки, диоды и другие нелинейные элементы. В задачах требуется найти ток в какой-либо ветви, падение напряжения на элементе, заряд на обкладке, сопротивление на участке и т.д. В связи с этим возникает вопрос о методах, оптимальных для конкретных задач.

Методы решения задач могут быть аналитические (получение выражения-формулы для искомой величины), графические (точные или приближенные вычисления с использованием графиков – ВАХ, временных зависимостей и др.).

Существует множество способов расчета электрических цепей, состоящих из батарей и резисторов [ 1 ]. Практически любой из них годится и для цепей батарей и конденсаторов, а при переходе к комплексным числам – и для цепей переменного тока.

Рассмотрим простые способы расчета ЭЦ постоянного тока, состоящих из резисторов и источников питания.

Методические рекомендации учителям по преподаванию сложной темы

Поскольку преподаваемый раздел подразумевается для углубленного изучения физики, то нет необходимости объяснять школьникам азы физики постоянного и переменного тока. Однако напомнить ребятам некоторые моменты будет все же полезно. К таким моментам относятся: законы параллельного и последовательного соединения элементов (соотношения для токов и напряжений на элементах), закон Ома для участка цепи и закон Ома для полной цепи [ 2 ], закон сохранения энергии (баланс мощности, выделяемой в цепи), закон Джоуля-Ленца. Полезным будет вспомнить об идеальных и реальных амперметре и вольтметре [ 3 ], активном и реактивном сопротивлениях.

Активное и реактивное сопротивление

СОПРОТИВЛЕНИЕМ в электротехнике называется величина, которая характеризует противодействие участка цепи электрическому току. Оно обусловлено преобразованием электрической энергии в другие типы энергии.

В ЭЦ имеется необратимое изменение энергии и передача энергии между участниками электрической цепи. При необратимом изменении электроэнергии участка цепи в другие виды энергии СОПРОТИВЛЕНИЕ элемента является АКТИВНЫМ, а п ри осуществлении обменного процесса электроэнергией между элементом цепи и источником – РЕАКТИВНЫМ [ 4 ].

Электрическая энергия в элементе может преобразовываться в тепловую, световую, механическую и другие виды энергии, таким образом, элемент, в котором происходит это НЕОБРАТИМОЕ преобразование, обладает АКТИВНЫМ СОПРОТИВЛЕНИЕМ.

В индуктивном элементе (катушке индуктивности или резисторе, скрученном в спираль), электрический ток создает магнитное поле. Под воздействием переменного тока в элементе возникает ЭДС самоиндукции, которая препятствует изменению магнитного потока в элементе (закон Фарадея), и, таким образом, имеет РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ.

Аналогичный обмен энергией происходит между источником ЭДС и конденсатором при протекании переменного тока. Конденсатор заряжается и разряжается, что означает протекание тока в цепи и, соответственно, РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ.

Индуктивный и емкостной элемент (иногда это не конденсаторы и катушки, а паразитные емкости и индуктивности участка цепи, имеющего скрутки и близкие расположения проводников) в цепи переменного тока работают какое-то время как потребители энергии (накапливая магнитное и электрическое поле), а какое-то время являются эффективными генераторами, возвращая и преобразуя накопленную энергию обратно в цепь в виде электричества.

Активное сопротивление

При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, которое обратно в электрическую энергию не превращается [ 5 ]. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.

Отличительной чертой элементов, имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле.

Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.

Реактивное сопротивление

Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.

Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока. Сопротивление конденсатора можно рассчитать по формуле

Треугольник сопротивлений

На диаграмме это выражение можно представить в виде ТРЕУГОЛЬНИКА СОПРОТИВЛЕНИЙ (считая резистивный, индуктивный и емкостной элементы соединенными последовательно):

Обобщение информации

Для обобщения представленных сведений можно вместе с ребятами составить и проанализировать следующую таблицу (табл. 3.1).

Соотношения токов и напряжений на элементах цепи при их последовательном и параллельном подключении.

Метод эквивалентных схем

Другие названия метода эквивалентных схем (МЭС), встретившихся автору работы в книгах и на просторах интернет: метод эквивалентных преобразований, метод свертывания. Здесь будем использовать аббревиатуру – МЭС.

Суть метода эквивалентных схем

Метод эквивалентных схем (МЭС) заключается в том, что исходную схему электрической цепи надо УПРОСТИТЬ, для чего ее необходимо представить в виде последовательных участков, на каждом из которых соединение элементов схемы либо последовательно, либо параллельно. Под УПРОЩЕНИЕМ СХЕМЫ будем понимать соединение или разъединение каких-либо узлов схемы, удаление или добавление резисторов, конденсаторов, добиваясь того, чтобы новая схема, состоящая из последовательно и параллельно соединенных элементов, была эквивалентна исходной.

Эквивалентная схема – это такая схема, в которой токи и напряжения на соответствующих участках такие же, как в исходной схеме. В этом случае все расчеты производятся с преобразованной схемой.

МЭС годится для сравнительно простых цепей (что считать простыми ЭЦ?), поэтому применяется сравнительно редко, так как далеко не каждую цепь можно упростить. Последовательно и параллельно соединенные резисторы заменяем их эквивалентами, шаг за шагом упрощая схему. После того, как найдены токи в цепи, выполняется обратное преобразование – развертывание цепи к исходной, с нахождением токов в элементах.

Для получения эквивалентной схемы цепи со сложным смешанным соединением элементов можно воспользоваться несколькими приемами [ 6 ]:

метод эквипотенциальных узлов;

метод исключения участков цепи;

метод «размножения» узлов;

метод расщепления ветвей;

Рассмотрим некоторые из этих методов.

Метод соединения эквипотенциальных узлов

Этот способ заключается в том, что в симметричных схемах отыскиваются узлы с равными потенциалами (ЭКВИПОТЕНЦИАЛЬНЫЕ УЗЛЫ). Эти узлы соединяются между собой, причем, если между этими точками был включен какой-то участок схемы, то его отбрасывают, так как из-за равенства потенциалов на концах ток по нему не течет и этот участок никак не влияет на общее сопротивление схемы [7].

Таким образом, замена нескольких эквипотенциальных узлов одним приводит к более простой эквивалентной схеме.

Рассмотрим примеры решения задач этим методом.

Задача «Мост»

Решение:

В силу симметрии ветвей цепи точки С и D являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и D соединяем в один узел. Получаем очень простую эквивалентную схему:

Задача «Звезда»

Решение:

Линия BF делит звезду на две симметричные части. Найдем эквипотенциальные точки. В точках потенциалы равны, значит сопротивление между ними можно отбросить. Эквивалентная схема выглядит так:

Сопротивления участков и равны, а эти участки подключены параллельно друг другу. Сопротивление каждого из них найти легко:

Задача «Звезда в треугольнике»

Решение:

Точки С и D имеют равные потенциалы, т.к. линия С D – ось симметрии схемы. Исключением сопротивление между ними. Получаем эквивалентную схему:

Задача «Куб»

Решение:

Рекуррентный метод

Рекуррентным называется метод, при котором задача решается по шагам, причем на каждом следующем шаге используются результаты, полученные на предыдущих шагах. Этот метод становится удобным, когда схема имеет повторяющиеся элементы и число элементов цепи велико [12].

Особую группу образуют задачи на расчет эквивалентных сопротивлений бесконечных цепей. Как правило, эти цепи симметричны и во многих случаях содержат одинаковые элементы (резисторы). Рассматриваемые задачи можно разбить на три группы: а) линейные (одномерные); б) плоскостные (двумерные); в) объемные (трехмерные). Последние два типа задач решаются только с помощью искусственного приема [ 7 ], содержание которого будет рассмотрено в следующей типичной задаче [ 8 ].

Задача «Бесконечная цепь»

Решение

Выделим в этой цепи бесконечно повторяющееся звено, оно состоит в данном случае из трех первых сопротивлений. Если мы отбросим это звено, то полное сопротивление бесконечной цепи от этого не изменится, так как получится точно такая же бесконечная цепь.

Так же ничего не изменится, если мы выделенное звено подключим обратно к бесконечной цепи, но при этом следует обратить внимание, что часть звена и бесконечная цепь сопротивлением R соединены параллельно. Таким образом получаем эквивалентную схему:

Для этой схемы находим полное сопротивление:

Задача «Челюсти»

Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки, которая состоит из одинаковых проволочных резисторов сопротивлением r каждый [13].

Решение

Эквивалентная схема представлена на рисунке.

Двигаясь по эквивалентной схеме справа налево, получим сопротивления:

Преобразуя последнее уравнение, получаем:

Откуда следует, что

Отрицательный корень уравнения не имеет смысла. Окончательный результат:

Задача «Вагоны»

Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки, которая состоит из одинаковых проволочных резисторов сопротивлением r каждый [13].

Решение

Чтобы найти эквивалентное сопротивление цепи, необходимо сначала выделить общую секцию, которая бесконечно повторяется. Понятно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится. Выделить повторяющуюся секцию в рассматриваемой цепи можно, но заменить сопротивление остальной части цепи искомым сопротивлением R _х нельзя, т.к. оставшаяся часть схемы имеет четыре соединительных провода. Если посмотрим на каркас слева, то получим изображение цепи в перспективе, приведенное на рисунке:

Полученная схема является бесконечной, и при исключении внешней рамки, содержащей точки А и В, мы получим схему с таким же сопротивлением. Нарисуем эквивалентную схему.

Метод размножения узлов

Иногда бывает целесообразнее замена одного узла несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части цепи.

Задача «Решетка»

Решение:

Поэтому достаточно рассчитать сопротивление одной из них: Тогда полое искомое сопротивление

Метод расщепления ветвей

Помимо метода размножения узлов, известен еще и метод расщепления ветвей. Обычно несколько параллельных и последовательных ветвей заменяют одной эквивалентной ветвью, но иногда можно сделать и наоборот – не объединить ветви, а расщепить.

Покажем на примере [12].

Задача «Конвертик»

Решение

Сопротивление на участках ОС ₁ B и O C ₂ D одинаковы и равны, как легко подсчитать, по 3r. Новая эквивалентная схема:

Сопротивление на участке AOB (не включая участок АО) равно сопротивлению на участке AОD (не включая участок АО). Найдем эти сопротивления:

Окончательная эквивалентная схема будет состоять из трех параллельно соединенных сопротивлений:

Ее общее сопротивление равно

Метод Кирхгофа непосредственный

Суть метода

Этот метод является универсальным, но расчет вручную возможен для не слишком сложных схем. Для сложных ЭЦ применяется машинный счет. Очень удачное методическое пособие [ 12 ], в котором методом Кирхгофа решаются задачи на разветвленные цепи переменного тока с резистивными, емкостными и индуктивными элементами (в том числе со взаимными индуктивностями) с поясняющими примерами и применением машинного счета, приведена в [18]. Для ученика этот материал может оказаться довольно сложным, поскольку составлялся для студентов 3 курса физ-теха, а для учителя – максимально полезным при освоении этой трудной темы.

Алгоритм решения задач по правилам Кирхгофа

На схеме ЭЦ задаются направления токов во всех ВЕТВЯХ цепи.

Задаются направления обхода контуров

Для узлов схемы (всех, кроме одного любого) составляются уравнения по первому правилу Кирхгофа

Для контуров схемы (всех, кроме одного) составляются уравнения по второму правилу Кирхгофа.

Число независимых уравнений должно быть равно числу неизвестных.

Рассмотрим подробнее правила Кирхгофа.

Первое правило Кирхгофа

УЗЕЛ – это точка соединения ВЕТВЕЙ (см. рис. 3.1.).

ВЕТВЬ – это участок РАЗВЕТВЛЕННОЙ электрической цепи, содержащий один или несколько последовательно соединенных элементов, или, иначе говоря – это участок цепи между двумя узлами.

Первое правило Кирхгофа – это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает.

Второе правило Кирхгофа

Для начала нужно выбрать направления токов в ЭЦ и задать стрелкой направление обхода контура (см. рис. 3.1).

Второе правило Кирхгофа гласит:

Если направление обхода контура совпадает с направлением увеличения потенциала ЭДС, то ЭДС берется со знаком «плюс», в противном случае – со знаком «минус».

Если направление тока совпадает с направлением обхода контура, то ток берется со знаком «плюс», в противном случае – со знаком «минус».

КОНТУРОМ называется замкнутый путь от узла по ветвям ЭЦ до этого же узла (см. рис.3.1).

Поясняющий пример

Поясним правила по применению метода Кирхгофа для ЭЦ, представленной на рис. 3.1.

По первому правилу Кирхгофа имеем для токов в УЗЛАХ:

Из узла А все токи вытекают, а в узел D все токи втекают в соответствии с выбранными нами направлениями токов (красные стрелочки на рисунке).

По второму правилу Кирхгофа имеем для алгебраической суммы напряжений в КОНТУРАХ:

В каждой из систем одно из уравнений является линейной комбинацией остальных, поэтому достаточно взять на одно уравнение меньше в каждой системе. Например, для ЭЦ, содержащей М узлов, нужно записать только (М-1) уравнений для токов по первому правилу Кирхгофа, и (К-1) уравнение по второму правилу Кирхгофа, если цепь содержит К контуров.

Чем более разветвленной является цепь, тем больше уравнений и неизвестных содержит система, и тем более громоздкими могут оказаться вычисления. Однако метод довольно прост в применении и годится для цепей постоянного и переменного тока, содержащих активные и реактивные элементы.

Решение задачи сводится к решению объединенной системы линейных уравнений для токов и напряжений и поиску искомых величин. Если в ответе один из токов получается с отрицательным знаком, то, значит, направление тока противоположно тому, что было выбрано на схеме. Таким образом, на правильность ответа в задаче выбор направления токов и обхода контуров не влияет. Правильность полученного ответа можно проверить с помощью баланса мощностей.

Методическое пособие [ 13 ], в котором приведены олимпиадные задачи на правила Кирхгофа, доступно для скачивания (ссылка в списке использованных источников).

Решение олимпиадных задач методом Кирхгофа

Несколько задач из этого сборника [19] решим здесь.

Задача 1 из [19]

Решение

Поясняющие схемы к задаче 4

Составим уравнения по второму правилу Кирхгофа. (Первым правилом Кирхгофа мы уже воспользовались в уме, когда выражали ток верхнего ЭДС через ток нижнего ЭДС и амперметр.) Наша цепь содержит три контура (верхний, нижний, и большой внешний), поэтому уравнений по второму правилу Кирхгофа будет по два для каждого случая.

Задача 2 из [19]

Решение

Составим уравнения по второму правилу Кирхгофа. (Первым правилом Кирхгофа мы уже воспользовались в уме, когда выражали ток верхнего ЭДС через ток нижнего ЭДС и амперметр.) Наша цепь содержит три контура (верхний, нижний, и большой внешний), поэтому уравнений по второму правилу Кирхгофа будет два.

Посмотрим, что будет в случае, если учесть внутренние сопротивления источников и амперметра. Обозначим их через для верхнего, нижнего источников и амперметра, соответственно.

Система уравнений примет вид:

Решение для тока через амперметр в этом случае имеет вид:

Считая сопротивления источников и амперметра малыми по сравнению с сопротивлениями резисторов, можно пренебречь последним слагаемым в знаменателе ввиду его малости.

Для упрощения записи примем обозначения:

Тогда разность токов выразится так:

Вводя новые обозначения:

Баланс мощности

Для проверки правильности решения задачи и полученных соотношений для токов и напряжений на элементах цепи, применяют уравнение БАЛАНСА МОЩНОСТИ, которое является следствием законом сохранения энергии:

суммарная мощность, вырабатываемая (генерируемая) источниками электрической энергии, равна сумме потребляемых в цепи мощностей.

Источники ЭДС вырабатывают электрическую энергию, если направления тока в ветви и увеличения потенциала соответствующего источника ЭДС совпадают, а если направления ЭДС и тока направлены в противоположно друг другу, то источник ЭДС потребляет энергию и его мощность записывают со знаком минус (так бывает в случае, когда в задаче учитывается внутреннее сопротивление истоника ЭДС).

Поясним примером. Для этого в схеме, представленной на рис. 3.1, зададим параметры цепи, найдем токи во всех ветвях и проверим правильность решения задачи с помощью баланса мощности.

Решение задачи по методу Кирхгофа с проверкой баланса мощностей

Найдите токи во всех ветвях электрической цепи, представленной на рис. 3.1, для следующих параметров:

Решение

Для выбранных на рис. 3.1. направлений токов и обходов контуров составим систему линейных уравнений относительно неизвестных токов и решим в общем виде.

При переходе ко второй системе мы учли условия задачи Решение системы в общем виде выражается так:

Подставляя данные в полученные выражения для токов, находим их (округляя до сотых):

Как видим, мы не «угадали» с направлением только одного тока – текущего в нижней ветви цепи. Анализируя рис. 3.1 и полученные значения для токов, заключаем, что источник ЭДС в ветви AD генерирует электрическую мощность (направление тока совпадает с направлением возрастания потенциала ЭДС, найденный ток в этой ветви отрицательный и направлен противоположно стрелочке на рисунке). Источник ЭДС в ветви BD является потребителем электрической энергии, наряду с резисторами в цепи, так как направление тока в нем противоположно направлению возрастания потенциала ЭДС.

Т.е. работу по перемещению зарядов в данной цепи выполняет нижний источник ЭДС, а правый источник ЭДС этому препятствует.

Проверим правильность решения задачи, составив уравнение БАЛАНСА МОЩНОСТЕЙ. В одной части уравнения представим суммарную мощность, выделяемую источниками, в другой части – суммарную мощность, потребляемую резисторами. В общем виде для нашей схемы уравнение примет вид:

В левой части уравнения стоят знаки «минус», так как для обоих источников ЭДС направления тока на схеме и направления ЭДС (точнее, направление увеличения потенциала ЭДС) противоположны. Подставляя числа, получим:

Как видим, баланс мощностей выполняется (с учетом погрешности на округление), значит, токи найдены верно.

Метод контурных токов

Суть и алгоритм метода

КОНТУРНЫЙ ТОК – это величина, которая одинакова во всех ветвях данного контура.

ДЕЙСТВИТЕЛЬНЫЙ ТОК в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

КОНТУРНАЯ ЭДС – это сумма всех ЭДС входящих в этот контур.

СОБСТВЕННЫМ СОПРОТИВЛЕНИЕМ контура называется сумма сопротивлений всех ветвей, которые в него входят.

ОБЩИМ СОПРОТИВЛЕНИЕМ контура называется сопротивление ветви, смежное двум контурам.

Общий алгоритм составления уравнений:

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Рассмотрим метод контурных токов на примере задачи < Задача 1 из [19] >, решенной выше по методу Кирхгофа.

Решение задачи < Задача 1 из [19] >методом контурных токов

Электрическую схему для решения задачи по методу контурных токов нарисуем в следующем виде (можно сравнить с рис. 3.2).

Схема с выбранными контурными токами (зеленые стрелки) и действительными токами в ветвях (красные стрелки).

Решая систему уравнений, находим контурные токи, а затем и действительные, по алгоритму, описанному выше.

Метод наложения

Наряду с методом контурных токов для анализа электрических цепей используется другой метод, основанный на принципе наложения, который применяется только к линейным системам.

Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою лепту в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником).

Порядок расчета [14]:

2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой.

3 – Алгебраическое суммирование всех частичных токов, для нахождения токов в исходной цепи.

Метод узловых потенциалов

Суть метода узловых потенциалов (МУП)

Согласно закону сохранения энергии, ток на этом участке равен

откуда видно, что для нахождения токов в каждой из ветвей достаточно знать потенциалы на ее концах (точнее — разности потенциалов). Точки соединения неразветвленных участков цепи (ВЕТВЕЙ) называют УЗЛАМИ, отсюда и название способа — метод узловых потенциалов.

Таким образом, в качестве неизвестных величин для составления уравнений, выбирают потенциалы узлов схемы. Удобно потенциал одного из них (любого) принять равным нулю. Тогда потенциалы остальных узлов будут равны напряжениям, измеренным относительно выбранного нами узла. Уравнения для определения узловых потенциалов записываются для токов, которые втекают в узлы и вытекают из них: сумма втекающих в узел токов равна сумме вытекающих.

Покажем несколько задач с подробным решением на применение МУП.

Задачи с применением МУП

Задача «Перемычка без резистора»

В схеме на рис. 1 найти ток через перемычку АВ [ 14 ].

Решение

Упростим схему, заменив параллельно соединенные резисторы 1 и 3, а также 2 и 4 их эквивалентами. Получится простая цепь с общим сопротивлением

Напряжения на резисторах 1 и 3 равны, значит,

Теперь найдем ток через перемычку АВ.

Рассмотренный метод хотя и прост, но очень громоздок. Кроме того, он не универсален — далеко не всякую схему удается так упростить. Например, если на рисунке 1 заменить перемычку резистором, в получившейся схеме не окажется ни параллельно, ни последовательно соединенных резисторов, и это уже совсем другая задача.

Задача «Параллельные ЭДС»

Решение

Из этого уравнения находим потенциал точки В:

Ток через резистор

Задачу к представленной схеме можно сформулировать иначе (см. следующий параграф).

Задача «Поиск эквивалентного ЭДС»

Можно ли параллельно соединенные источники с ЭДС с внутренними сопротивлениями заменить эквивалентным источником? Если можно, то каковы должны быть его ЭДС и внутреннее сопротивление? [ 20 ]

Решение

Для ответа на эти вопросы нужно попытаться выражение, полученное в предыдущей задаче для тока нагрузки, привести к виду

Сравним его с выражением для тока нагрузки, полученным в предыдущей задаче:

Соответствующая эквивалентная схема электрической цепи будет выглядеть так:

Можно доказать, что любую систему, состоящую из источников питания и резисторов, подключенную двумя проводами к внешней цепи, можно заменить эквивалентной схемой.

Задача 3 «Перемычка с резистором»

В схеме, изображенной на рисунке, найдите сопротивление между точками А и В. [20]

Решение

Как видим, в этой системе уравнений три неизвестных: потенциалы в указанных точках и ЭДС источника, который мы ввели искусственно для решения задачи.

Решая систему для заданных сопротивлений, находим потенциалы в точках:

Ток, протекающий через узел А (или В, т.к. это точки в одной ветви), находится сложением токов, протекающих через два правых резистора (направления токов на схеме показаны красными стрелочками). Математически это выглядит следующим образом:

В ситуации, когда сопротивления резисторов заданы иначе, не пропорциональны друг другу, последовательность рассуждений сохраняется, но выражения для потенциалов, токов и общего сопротивления могут быть более громоздкими.

Для схем с конденсаторами идея расчета та же, но вместо токов узлов нужно рассматривать заряды проводников, соединенных с узлом.

Задача 4 «Конденсаторы»

Рассчитайте заряды конденсаторов в схеме, приведенной на рисунке. [20]

Решение

Обозначим. (рис. 8) и расставим предполагаемые знаки зарядов обкладок конденсаторов (это можно сделать произвольно, как и для направлений токов в предыдущих примерах. Если знак заряда в ответе получится отрицательным, то, значит, е угадали со знаком при задании зарядов на обкладках). Если конденсаторы вначале не были заряжены, то можно записать:

Теперь легко найти заряды каждого из конденсаторов.

Выше мы рассмотрели линейные цепи, содержащие резисторы или конденсаторы, но этот метод годится также и для расчета и нелинейных цепей. Продемонстрируем на примере.

Задача «МУП для нелинейных цепей»

Найдите ток через нелинейный элемент, для которого зависимость тока от напряжения имеет вид:. [20]

Решение

Тогда для узла В получим уравнение:

МУП можно пользоваться и в случае, когда ВАХ нелинейного элемента задана графически. В этом случае полученную при решении уравнений зависимость между током элемента и потенциалом узла нужно изобразить на том же графике, где приведена ВАХ, и найти точку пересечения графиков, т. е. решить уравнение графически.

Задача «После замыкания»

Какой заряд протечет через батарею (рис. 11)‚ если точки А и В замкнуть перемычкой? [20]

Решение

Расставим знаки и значения предполагаемых зарядов на обкладках конденсаторов, учитывая, что участки цепи, содержащие точки А и В, имеют нейтральный заряд, обкладки одного конденсатора имеют равные по модулю и противоположные по знаку заряды, а также учитывая знаки потенциалов батареи.

Шаг 1. Найдем потенциалы точек А и В, приняв потенциал точки D за 0, а точки С за :

Найдем заряды на обкладках и потенциалы точек А и В:

Шаг 2. Найдем заряды конденсаторов и потенциалы точек А и В после замыкания перемычки АВ.

После замыкания АВ потенциалы этих точек уравняются, знаки зарядов на конденсаторах останутся прежними, а модули зарядов изменятся (см. рис.). На обкладках конденсаторов, контактирующих с ЭДС, произойдет перераспределение зарядов, и через батарею протечет электрических ток (заряд). На внутренних обкладках, контактирующих с АВ, суммарный заряд останется нейтральным. Тогда заряды на обкладках «было»-«стало» будут удовлетворять соотношениям:

Аналогично, разности потенциалов на правых конденсаторах равны, тогда мы можем записать:

Задача «Перемычка с конденсатором»

Решение

Рассуждения и шаг 1 такие же, как в предыдущей задаче. Таким образом, при разомкнутой ветви АВ имеем:

.

Составим систему уравнений и решим ее методом матриц относительно неизвестных зарядов:

Таким образом, заряды всех конденсаторов после подключения конденсатора АВ, найдены. Задача решена.

Завершение модуля

Мы рассмотрели одни из самых популярных методов решения задач на электрические цепи. Многообразие задач неисчерпаемо, поэтому данный модуль будет развиваться, наполняться новыми методами, еще не рассмотренными здесь, и новыми интересными задачами.

В завершение модуля рекомендуется провести тематическую мини-олимпиаду в соответствии с расписанием. После объявления результатов – обсуждение решений и рефлексия.

Основные результаты выполненной работы можно сформулировать следующим образом.

Проведено исследование состояния дистанционного образования в Ульяновской области и проведен мониторинг работы с одаренными детьми. Сделан вывод о высоком потенциале одаренности в УО и сформулирован план региональных мероприятий, направленных на улучшение результатов школьников на межрегиональном и международном уровне.

Проведен аналитический обзор существующих методов решения задач со сложными электрическим цепями, представлен теоретический (методы решения) и практический (задачи с решениями, некоторые – авторские) материалы для учителя и школьника.

Разработан модуль обучения «Сложные электрические цепи» (раздел 3)

При участии автора в регионе запущены проекты:

– Сообщество Клуб юных физиков «КлЮФ» (https://vk.com/klyuff);

– Студия «Уроки настоящего г. Ульяновск» (https://vk.com/club_ulapo);

Проходят регулярные онлайн- и офлайн-встречи «олимпиадников» в «Точке кипения. Ульяновск».

Планы автора по развитию данной темы

Работа с одаренными детьми и подготовка к занятиям позволяет учителям быть «в тонусе», постоянно учиться и развиваться. И хотя эта работа требует много ресурсов (временных, физических), она же и обогащает наставника и его подопечных интеллектуально и эмоционально во время общения, достижения результатов, маленьких открытий. Дети из отдаленных уголков нашего региона, как бывает часто, лишены такого личного общения с наставником, поэтому хорошей траекторией их развития может стать дистанционное обучение, когда есть связь с наставником из регионального центра и занятия носят регулярных характер.

Задача-максимум на ближайший год – наладить систему дистанционного образования по физике и тьюторского сопровождения одаренных детей в регионе на платформе «Архитектор талантов» (система прошла тестовый режим).

Выражаю искреннюю благодарность ОЦ «Сириус» за идею программы «Большие вызовы», за возможность участвовать в ней мотивированным учителям из регионов, за создание сообщества учителей, работающих в регионах с одаренными детьми, а также за опыт взаимодействия с лучшими наставниками страны.

Благодарю Фонд поддержки талантов Ульяновской области за привлечение меня к работе с одаренными детьми – это оказалось очень увлекательным и развивающим процессом.

Благодарю своих учеников из 20 лицея, моих юных физиков, за помощь в подборке тематических задач, обсуждение их решений, за сложные вопросы и стимул больше узнавать.

Благодарю научного руководителя – Юдина Ивана Сергеевича – за интересные семинары, качественное наставничество и ценный практический опыт.

1 А.Ф. Газизуллина. Рекомендации по решению нетрадиционных задач на расчет электрических цепей постоянного тока

2 ЭДС. Закон Ома для полной цепи.

3 В.В. Ефимов. Идеальные и реальные вольтметры и амперметры в цепях постоянного тока//Физика, с.28-39.

4 Активное и реактивное сопротивление

5 Активное и реактивное сопротивление

6 А. Хацет. Методы расчета эквивалентных сопротивлений//Журнал Квант. 1972. №2. С. 54-59.

7 Задачник олимпиадника http://fizportal.ru/electric-current-8

8 Методы расчета резисторных цепей

9 Форум МАИ. Задачи на бесконечные резистивные цепи. https://club443.ru/arc/index.php?showtopic=131763

10 Форум. Бесконечные цепи.

1.12 Курганов С.Б., Новиков С.Г., Сабитов О.Ю. Сборник задач по ТОЭ с примерами решения на MathCad. Изд-во Ульяновского государственного университета, 2004 г. https://www.twirpx.com/file/18962/

13 И.В. Яковлев. Материалы по физике. Правила Кирхгофа

Источник