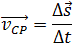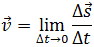Что называется скоростью физика

Кинематика. Скорость.

Скорость характеризует быстроту любых изменений в окружающем мире. Распространение звука или света в воздухе, движение облаков, испарение воды, полет птиц, движение пешеходов по улице – все явления характеризуются определенно скоростью.

Скорость – векторная физическая величина, характеризующая не только быстроту перемещения тела, но и направление его движения.

Скоростью точки называется предел отношения перемещения к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении Δt к нулю:

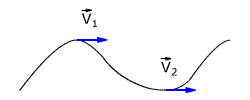
Такое определение скорости называют также мгновенной скоростью. Оно справедливо и для любых видов движения. Вектор мгновенной скорости всегда направлен по касательной к траектории движения, указывая направление, по которому происходило бы движение тела, если бы с момента времени t на него прекратилось действие других тел.

Понятие средней скорости вводится для характеристики неравномерного движения (движения с переменной скоростью). Определяется она скалярно или векторно.

Когда средняя скорость тела υ_ср равна отношению всего пути Δs ко всему времени движения Δt, то Здесь пройденный путь и время – скалярные величины, следовательно скорость тоже величина скалярная.

Когда средняя скорость тела равна отношению перемещения точки к промежутку времени, в течение которого это перемещение произошло, то Здесь средняя скорость перемещения – векторная величина.

Для неравномерного криволинейного движения векторное определение средней скорости не всегда позволяет определить реальные скорости на пути движения тела. Например, при движении тела по замкнутой траектории в течение некоторого времени его перемещение равно нулю, хотя скорость была отлична от нуля. В таком случае лучше пользоваться скалярным определением скорости.

Источник

Скорость

Ско́рость (часто обозначается , от англ. velocity или фр. vitesse ) — векторная физическая величина, характеризующая быстроту перемещения и направления движения материальной точки в пространстве относительно выбранной системы отсчёта (например, угловая скорость). Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке используется также скорость в широком смысле, как быстрота изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще изменения во времени, но также в пространстве или любой другой). Так, например, говорят о скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения, угловой скорости и т. д. Математически характеризуется производной функции.

Содержание

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора этой точки:

Здесь — модуль скорости, — направленный вдоль скорости единичный вектор касательной к траектории в точке .

Скорость направлена вдоль касательной к траектории и равна по модулю производной дуговой координаты по времени.

Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю) и тогда:

Скорость — характеристика движения точки, при равномерном движении численно равная отношению пройденного пути s к промежутку времени t, за который этот путь пройден.

Следует различать координатную и физическую скорости. При введении криволинейных или обобщённых координат положение тел описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями.

Мгновенная и средняя скорость

Следует отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Когда говорят о средней скорости, для различения, скорость согласно выше приведённому определению называют мгновенной скоростью.

Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

В полярных координатах

Проекции скорости в декартовой системе координат

В то же время , поэтому

Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки:

.

Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна , а скорость системы отсчёта S’ относительно системы отсчёта S равна , то скорость тела при переходе в систему отсчёта S’ будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношения между единицами скорости

См. также

Скорости волн
Групповая скорость | Фазовая скорость | Фронтовая скорость | Сигнальная скорость

Полезное

Смотреть что такое «Скорость» в других словарях:

СКОРОСТЬ — СКОРОСТЬ, скорости, мн. и, скоростей, жен. 1. только ед. (мн. спец.). Та или иная степень быстроты движения. Поезд двигался с большой скоростью. Автомобиль развил бешеную скорость. Эксплоатационная скорость поезда. Поставить рекорд скорости.… … Толковый словарь Ушакова

СКОРОСТЬ — в механике, одна из осн. кинематич. характеристик движения точки; величина векторная, определяемая равенством: v=dr/dt, где r радиус вектор точки, t время. При равномерном движении С. точки численно равна отношению пройденного пути s к промежутку … Физическая энциклопедия

СКОРОСТЬ — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Современная энциклопедия

Скорость — СКОРОСТЬ, характеристика поступательного движения точки (тела), численно равная при равномерном движении отношению пройденного пути s к промежуточному времени t, то есть v= s/t. При вращательном движении тела пользуются понятием угловой скорости … Иллюстрированный энциклопедический словарь

СКОРОСТЬ — СКОРОСТЬ, и, мн. и, ей, жен. 1. Степень быстроты движения, распространения, действия. Развить с. Рекорд скорости бега. Двигаться на больших скоростях. С. звука (скорость распространения звуковых волн в среде). С. света (скорость распространения… … Толковый словарь Ожегова

скорость — скорость; мгновенная скорость Скорость точки жидкости, рассматриваемая как векторная функция переменных Эйлера … Политехнический терминологический толковый словарь

СКОРОСТЬ — СКОРОСТЬ, характеристика движения точки (тела), численно равная при равномерном движении отношению пройденного пути к промежутку времени, за которое этот путь пройден. Скорость (физическая) характеризует движение тела в определенном направлении,… … Научно-технический энциклопедический словарь

Скорость — Скорость, лазание на скорость вид скалолазания со следующими специфическими особенностями: большая протяженность большая высота, необходима страховка с веревкой на соревнованиях применяется верхняя страховка относительно несложные движения… … Энциклопедия туриста

Источник

Формула скорости — обозначение, единицы измерения и примеры нахождения

Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник

Скорость

Скорость – это количественная характеристика движения тела.

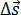
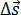
Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения Средняя скорость определяется по формуле:

Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения 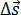к очень малому промежутку времени, за который это перемещение произошло.

Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).

Рис. 1.6. Вектор мгновенной скорости.

В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с. Часто скорость измеряют в других единицах. Например, при измерении скорости автомобиля, поезда и т.п. обычно используется единица измерения километр в час:

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том, что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта. Вагон, по которому идёт человек, является частью поезда.

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY, а с подвижной системой отсчёта – систему координат X_ПО_ПY_П (см. также раздел Система отсчёта). А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

Это закон сложения перемещений. В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Это закон сложения скоростей:

Источник