Что называется системой автоматического регулирования

Системы автоматического регулирования

В такой системе непрерывно идет обмен информацией между объектом и регулятором, воздействие передается от одного эле­мента регулятора к другому, последовательно меняя при этом свою физическую природу и уровень. Сформированное в результате регулирующее воздействие по своей природе может быть различно. Если, например, объект — электродвигатель привода подачи электродной проволоки, то регулирующее воздействие должно быть напряжением, подаваемым на его якорь; для сварочного источника питания регулирующее воздействие — это ток или напряжение, изменяемые в цепи управления.

Именно САР противодействует возмущениям, компенсирует, нейтрализует или ослабляет их вырабатываемыми встречными регулирующими воздействиями, обеспечивая заданное на каждый момент времени состояние объекта. Регулирование продолжается до тех пор, пока ошибка не становится меньше порога чувствительности системы.

Разнообразные САР отличаются одна от другой функциональными возможностями, принципами построения, конструктивной реализацией. По роду используемой энергии САР делят на электромеханические, электронные, пневматические, гидравлические, а также смешанного типа — электропневматические, электрогидравлические и др.

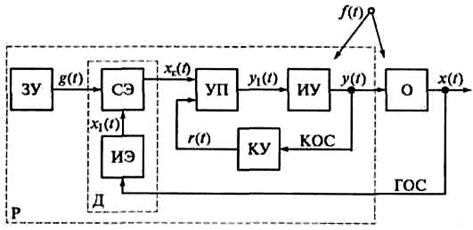
Все многообразие входящих в различные системы автоматики элементов по функциональному назначению может быть сведено в обобщенную функциональную схему САР (рисунок 5.4), состоящую из устройств, узлов, элементов, каждый из которых исполняет свою функцию в системе и графически изображается прямоугольниками, а также из связей между ними, изображаемых стрелками, указывающими направление прохождения сигналов (информации). Регулятор в таких схемах представляют в развернутом виде, а объект часто вообще опускают. Рассмотрим элементы САР.

Р — регулятор; ЗУ — задающее устройство; СЭ — сравнивающее устройство; ИЭ — измерительный преобразователь; Д — датчик; УП — усилитель-преобразо­ватель; КУ — корректирующее устройство; ИУ — исполнительное устройство; КОС — корректирующая обратная связь; О — объект; ГОС — главная обратная связь;

g(t) — задающее воздействие; f(t) — возмущение; x(t) — регулируемая величина; x₁(t), x_ε(t) — сигнал и ошибка регулируемой величины; y(t) — регулирующее воздействие; y₁(t) — сигнал регулирующего воздействия; r(t) — дополнительное воздействие

Рисунок 5.4 – Функциональная схема системы автоматического регулирования

1. Датчик, или измерительный преобразователь (элемент ИЭ), измеряет действительную регулируемую величину x(t) и преобразует ее в сигнал х₁(t), удобный для дальнейшего использования (чаще всего в ток или напряжение).

2. Задающее устройство (ЗУ) формирует требуемое на каждый момент времени задающее воздействие g(t) в удобном для сравнения с х₁(t) виде, имитирующее заданное значение регулируемой величины x(t).

4. Усилитель или усилитель-преобразователь (УП) усиливает и преобразует сигнал ошибки до величины y₁(t), достаточной и пригодной для управления исполнительным устройством (ИУ), преобразует входной сигнал количественно и (или) качественно, согласует вход исполнительного устройства с выходом СЭ по роду используемой энергии.

5. Исполнительное устройство под воздействием y₁(t) вырабатывает регулирующее воздействие y(t), поступающее на регулирующий орган (РО) объекта управления (О).

6. Корректирующее устройство (КУ) включают последовательно или параллельно названным элементам (на схеме показан пос­ледний вариант). Его назначение — улучшить качество регулиро­вания объекта с помощью формирующихся в них дополнитель­ных воздействий r(t).

Если выбранный для контролируемой системы параметр достаточно полно характеризует объект, то можно считать, что задача регулирования — поддерживать регулируемую величину на за­данном уровне. Это позволяет при дальнейшем рассмотрении САР не изображать на функциональных схемах объект.

Некоторые элементы автоматической системы в отдельных случаях могут отсутствовать, но главная обратная связь (ГОС) должна функционировать всегда, ибо с ее помощью выявляется соответствие действительного состояния объекта регулирования состоянию, заданному на данный момент времени. Наличие ГОС — основной признак САР.

Автоматическое регулирование — это автоматическое поддержание заданной регулируемой величины (переменной состояния) объекта путем постоянного контроля его состояния и действующих на него возмущений, а также регулирующего воздействия (при необходимости) на его регулирующий орган.

Управляющее воздействие может быть неизменным (системы автоматической стабилизации), в этом случае его называют установкой (например, система автоматического поддержания напряжения дуги путем изменения ее длины в установках аргонодуговой сварки неплавящимся электродом; система поддержания напряжения дуги путем изменения скорости подачи электродной проволоки в аппаратах для дуговой сварки типа АДС-1000-4; система поддержания постоянства частоты вращения обечайки, в которой фактическая скорость измеряется тахогенератором).

В системах программного регулирования управляющее воздействие изменяется программным устройством по заранее назначенной программе в функции времени или перемещения (положения). Такие системы используют, например, для регулирования параметров режима сварки (тока, скорости сварки, скорости подачи проволоки, амплитуды или частоты поперечных колебаний электрода) в зависимости от пространственного положения электрода в установках для сварки неповоротных стыков труб; в электрогазорезательной машине «Кристалл» с программным управлением, предназначенной для газовой или газоэлектрической резки листов из стали или цветных сплавов.

Если САР вместо функциональной зависимости воспроизводит на выходе изменения входного воздействия, причем чаще на более высоком уровне мощности (т.е. реализует простую пропорциональную зависимость), а управляющее воздействие заранее неизвестно, произвольно, то такую САР называют следящей системой. Их применяют при электронно-лучевой, а особенно при дуговой сварке стыков большой протяженности (или криволинейных) для автоматической ориентации электрода относительно изделия, когда уход стыка из-за коробления и дефектов сборки заранее неизвестен. Используют следящие системы в сварочных манипуляторах и роботах.

Известны также САР, обеспечивающие изменение регулируемой величины по производной, интегралу или более сложной функции от задающего воздействия и др.

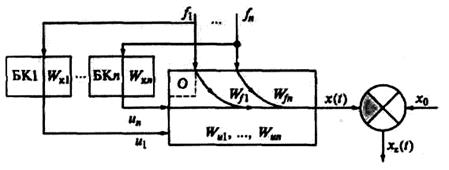
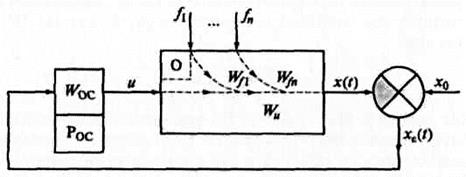
Поэтому принципы построения систем автоматического управления (САУ) вполне пригодны для различных по своей физической природе объектов управления. Если возмущающее воздействие при работе объекта может быть измерено в любой момент времени, то задача управления объектом может быть решена с помощью принципа компенсациивозмущения, действующего на систему (принцип разомкнутого управления по выходному параметру объекта). Этот принцип предполагает управление, основанное на возможности измерения возмущений f_n, действующих на объект управления, и их компенсации через СУ (рисунок 5.6).

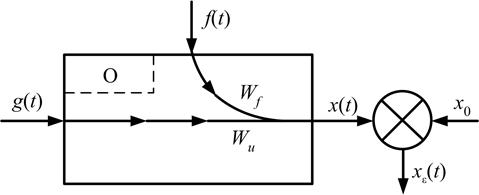
W_f и W_u — передаточные функции объекта соответственно по возмущению и по управлению; х₀ — установленное значение регулируемой величины; f(t) — возмущение; x(t) — регулируемая величина; x_ε(t) — ошибка регулируемой величины;

Рисунок 5.5 – Схема воздействий на объект управления

БК1. БКn — блоки компенсации; W_к1. W_кn — передаточные функции блоков компенсации; W_f и W_u — передаточные функции объекта соответственно по возмущению и по управлению; х₀ — установленное значение регулируемой величины; u₁. и_n — управляющие воздействия; f(t) — возмущение; x(t) — регулируемая величина; x_ε(t) —ошибка регулируемой величины

Рисунок 5.6 – Структурная схема системы управления по возмущению

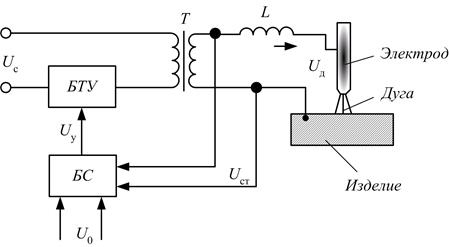
Примером построения САУ по принципу компенсации является система регулирования напряжения в сварочном трансформаторе с помощью контроля изменения напряжения питающей сети U_c (рисунок 5.7).

БТУ — блок тиристорного управления; БС — блок сравнения; L — индуктивность; U₀ — эталонная уставка по напряжению сети; U_y — сигнал управления; Û_ст — напряжение со вторичной обмотки трансформатора Т, I_д — ток дуги

Рисунок 5.7 – Система регулирования напряжения в сварочном трансформаторе при возмущении по напряжению сети U_c

Принцип компенсации обеспечивает высокое быстродействие системы регулирования. Однако при построении таких систем обычно ограничиваются выделением и компенсацией небольшого числа возмущений, играющих основную роль в отклонении регулируемой величины объекта от ее заданного значения, оставляя некомпенсированными все остальные возмущения.

Для устранения этого недостатка в теории построения СУ более широко применяют принцип обратной связи. Этот принцип предполагает управление, основанное лишь на изучении отклонения х_ε регулируемой величины х от ее заданного значения х₀ и непосредственно не связанное с измерением возмущений f₁. f_n, действующих на объект регулирования.

Для построения структурной схемы САУ замкнутой ОС (рисунок 5.8) необходимо, в отличие от САУ по возмущению (см. рисунок 5.6) лишь одно управляющее устройство — регулятор Р_ос с передаточной функцией W_oc

индекс ОС относится к блоку обратной связи; W_f1 и W_fn — передаточные функции объекта соответственно по возмущению и по управлению; х₀ — установленное значение регулируемой величины; f(t) — возмущение; x(t) — регулируемая величина; x_ε(t) — ошибка регулируемой величины; u — управляющее воздействие

Рисунок 5.8 – Структурная схема системы управления с обратной связью (принцип управления по отклонению)

К недостаткам принципа обратных связей следует отнести затруднения, возникающие в процессе разработки быстродействующих САУ, особенно для сложных инерционных объектов. Стремление повысить точность работы таких систем и увеличение коэффициента усиления регулятора Р₀с могут привести к потере устойчивости.

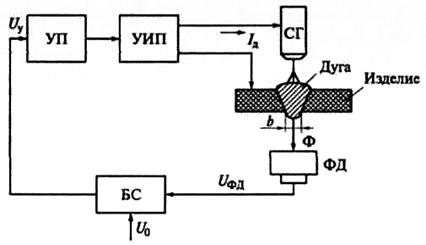
Пример применения принципа ОС в САУ сварочными процессами приведен на рисунке 5.9. Регулируемая величина в данном случае — ширина обратного валика b. Измерительное устройство величины b — это фотодатчик, устанавливаемый с обратной стороны изделия, при расплавлении последнего дугой.

ФД — фотодатчик контроля проплавления; УП — усилитель-преобразователь; УИП — управляемый источник питания дуги; СГ — сварочная горелка; U_фд — напряжение фотодатчика; Ф — световой поток; БС — блок сравнения; U₀ — эталонная уставка по напряжению сети; U_y — сигнал управления; I_д — ток дуги

Рисунок 5.9 – Система регулирования значения b — ширины обратного валика с фотодатчиком в цепи обратной связи

Недостатки САУ с ОС можно устранить созданием комбинированных автоматических систем управления, объединяющих оба отмеченных принципа управления (рисунок 5.10).

1 и 2 — контуры регулирования по возмущению и отклонению; Р_к — регулятор в блоке компенсации; Р_ос — регулятор в цепи обратной связи; х_к— сигнал компенсации; индекс ОС относится к блоку обратной связи; х₀ — установленное значение регулируемой величины; f(t) — возмущение; u — управляющее воздействие;

Рисунок 5.10 – Принципы комбинированного управления

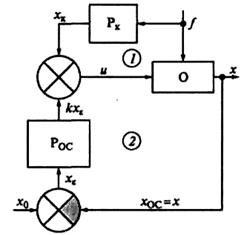
В подобных комбинированных системах основная тяжесть компенсации главного возмущения f, действующего на систему, ложится на регулятор Р_к. Точный регулятор Р_oс подавляет или ослабляет остальные возмущения, действующие на объект, и приводит действительное значение регулируемой величины х к заданной х₀. Пример использования комбинированного управления в сва­рочных установках приведен на рисунке 5.11. Принцип компенсации реализован в контуре 1, формирующем систему стабилизации напряжения на дуге U_aпри возмущениях по длине дуги l_д (при регулировании использована линейная связь U_д= кl_д). Контур 2 построен по принципу работы системы, представленной на рисунке 5.9. Регулируемая величина — это ширина обратного валика b.

1 и 2 — контуры регулирования по возмущению (длине дуги l_д) и отклонению (ширине обратного валика b); УУ1 — привод перемещения СГ по вертикали; УУ2 — устройство управления параметрами УИП по сигналу от датчика проплавления (ДП); U_вэ — уставка номинального параметра b; U_д.э — уставка по напряжению дуги; U_дп — сигнал на выходе ДП; УИП — управляемый источник питания дуги; СГ — сварочная горелка; Ф — световой поток; БС — блок сравнения; I_д — ток дуги.

Рисунок 5.11 – Система комбинированного управления параметрами сварочного процесса

Источник

Введение в теорию автоматического управления. Основные понятия теории управления техническим системами

Публикую первую главу лекций по теории автоматического управления, после которых ваша жизнь уже никогда не будет прежней.

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика привествуется.

1. Основные понятия теории управления техническими системами

1.1. Цели, принципы управления, виды систем управления, основные определения, примеры

Развитие и совершенствование промышленного производства (энергетики, транспорта, машиностроения, космической техники и т.д.) требует непрерывного увеличения производительности машин и агрегатов, повышения качества продукции, снижения себестоимости и, особенно в атомной энергетике, резкого повышения безопасности (ядерной, радиационной и т.д.) эксплуатации АЭС и ядерных установок.

Реализация поставленных целей невозможна без внедрения современных систем управления, включая как автоматизированные (с участием человека-оператора), так и автоматические (без участия человека-оператора) системы управления (СУ).

Определение: Управление – это такая организация того или иного технологического процесса, которая обеспечивает достижение поставленной цели.

Теория управления является разделом современной науки и техники. Она базируется (основывается) как на фундаментальных (общенаучных) дисциплинах (например, математика, физика, химия и т.д.), так и на прикладных дисциплинах (электроника, микропроцессорная техника, программирование и т.д.).

Любой процесс управления (автоматического) состоит из следующих основных этапов (элементов):

Для реализации Процесса Управления система управления (СУ) должна иметь:

Определение: Если система управления (СУ) содержит все перечисленные выше части, то она является замкнутой.

Определение: Управление техническим объектом с использованием информации о результатах управления называется принципом обратной связи.

Схематично такая система управления может быть представлена в виде:

Рис. 1.1.1 — Структура системы управления (СУ)

Если система управления (СУ) имеет структурную схему, вид которой соответствует рис. 1.1.1, и функционирует (работает) без участия человека (оператора), то она называется системой автоматического управления (САУ).

Если СУ функционирует с участием человека (оператора), то она называется автоматизированной СУ.

Если Управление обеспечивает заданный закон изменения объекта во времени независимо от результатов управления, то такое управление совершается по разомкнутому циклу, а само управление называется программным управлением.

К системам, работающим по разомкнутому циклу, относятся промышленные автоматы (конвейерные линии, роторные линии и т.д.), станки с числовым программным управлением (ЧПУ): см. пример на рис. 1.1.2.

Задающее устройство может быть, например, и “копиром”.

Поскольку в данном примере нет датчиков (измерителей), контролирующих изготавливаемую деталь, то если, например, резец был установлен неправильно или сломался, то поставленная цель (изготовление детали) не может быть достигнута (реализована). Обычно в системах подобного типа необходим выходной контроль, который будет только фиксировать отклонение размеров и формы детали от желаемой.

Автоматические системы управления подразделяются на 3 типа:

САР и СС являются подмножествами САУ ==> .

Определение: Автоматическая система управления, обеспечивающая постоянство какой-либо физической величины (группы величин) в объекте управления называется системой автоматического регулирования (САР).

Системы автоматического регулирования (САР) — наиболее распространенный тип систем автоматического управления.

Первый в мире автоматический регулятор (18-е столетие) – регулятор Уатта. Данная схема (см. рис. 1.1.3) реализована Уаттом в Англии для поддержания постоянной скорости вращения колеса паровой машины и, соответственно, для поддержания постоянства скорости вращения (движения) шкива (ремня) трансмиссии.

В данной схеме чувствительными элементами (измерительными датчиками) являются “грузы” (сферы). «Грузы» (сферы) также “заставляют” перемещаться коромысло и затем задвижку. Поэтому данную систему можно отнести к системе прямого регулирования, а регулятор — к регулятору прямого действия, так как он одновременно выполняет функции и “измерителя” и “регулятора”.

В регуляторах прямого действия дополнительного источника энергии для перемещения регулирующего органа не требуется.

В системах непрямого регулирования необходимо присутствие (наличие) усилителя (например, мощности), дополнительного исполнительного механизма, содержащего, например, электродвигатель, серводвигатель, гидропривод и т.д.

Примером САУ (системы автоматического управления), в полном смысле этого определения, может служить система управления, обеспечивающая вывод ракеты на орбиту, где управляемой величиной может быть, например, угол между осью ракеты и нормалью к Земле ==> см. рис. 1.1.4.а и рис. 1.1.4.б

1.2. Структура систем управления: простые и многомерные системы

В теории управления техническими системами часто бывает удобно систему разделить на набор звеньев, соединенных в сетевые структуры. В простейшем случае система содержит одно звено, на вход которого подается входной воздействие (вход), на входе получается отклик системы (выход).

В теории Управления Техническими Системам используют 2 основных способа представления звеньев систем управления:

— в переменных “вход-выход”;

— в переменных состояния (более подробно см. разделы 6…7).

Представление в переменных “вход-выход” обычно используется для описания относительно простых систем, имеющих один “вход” (одно управляющее воздействие) и один “выход” (одна регулируемая величина, см. рисунок 1.2.1).

Обычно такое описание используется для технически несложных САУ (систем автоматического управления).

В последнее время широкое распространение имеет представление в переменных состояния, особенно для технически сложных систем, в том числе и для многомерных САУ. На рис. 1.2.2 приведено схематичное представление многомерной системы автоматического управления, где u₁(t)…u_m(t) — управляющие воздействия (вектор управления), y₁(t)…y_p(t) — регулируемые параметры САУ (вектор выхода).

Рассмотрим более детально структуру САУ, представленную в переменных “вход-выход” и имеющую один вход (входное или задающее, или управляющее воздействие) и один выход (выходное воздействие или управляемая (или регулируемая) переменная).

Предположим, что структурная схема такой САУ состоит из некоторого числа элементов (звеньев). Группируя звенья по функциональному принципу (что звенья делают), структурную схему САУ можно привести к следующему типовому виду:

Рис. 1.2.3 — Структурная схема системы автоматического управления

Символом ε(t) или переменной ε(t) обозначается рассогласование (ошибка) на выходе сравнивающего устройства, которое может “работать” в режиме как простых сравнительных арифметических операций (чаще всего вычитание, реже сложение), так и более сложных сравнительных операций (процедур).

Задача системы управления состоит в том (если она устойчива), чтобы “работать” на уничтожение рассогласования (ошибки) ε(t), т.е. ==> ε(t) → 0.

Следует отметить, что на систему управления действуют как внешние воздействия (управляющее, возмущающее, помехи), так и внутренние помехи. Помеха отличается от воздействия стохастичностью (случайностью) своего существования, тогда как воздействие почти всегда детерминировано.

Для обозначения управляющего (задающего воздействие) будем использовать либо x(t), либо u(t).

1.3. Основные законы управления

Если вернуться к последнему рисунку (структурная схема САУ на рис. 1.2.3), то необходимо “расшифровать” роль, которую играет усилительно-преобразующее устройство (какие функции оно выполняет).

Если усилительно-преобразующее устройство (УПУ) выполняет только усиление (или ослабление) сигнала рассогласования ε(t), а именно: , где – коэффициент пропорциональности (в частном случае = Const), то такой режим управления замкнутой САУ называется режимом пропорционального управления (П-управление).

Если УПУ выполняет формирование выходного сигнала ε1(t), пропорционального ошибке ε(t) и интегралу от ε(t), т.е. , то такой режим управления называется пропорционально-интегрирующим (ПИ-управление). ==> , где b – коэффициент пропорциональности (в частном случае b = Const).

Обычно ПИ-управление используется для повышения точности управления (регулирования).

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t) и ее производной, то такой режим называется пропорционально-дифференцирующим (ПД-управление): ==>

Обычно использование ПД-управления повышает быстродействие САУ

Если УПУ формирует выходной сигнал ε₁(t), пропорциональный ошибке ε(t), ее производной, и интегралу от ошибки ==> , то такой режим называетсято такой режим управления называется пропорционально-интегрально-дифференцирующим режимом управления (ПИД-управление).

ПИД-управление позволяет зачастую обеспечить “хорошую” точность управления при “хорошем” быстродействии

1.4. Классификация систем автоматического управления

1.4.1. Классификация по виду математического описания

По виду математического описания (уравнений динамики и статики) системы автоматического управления (САУ) подразделяются на линейные и нелинейные системы (САУ или САР).

Каждый “подкласс” (линейных и нелинейных) подразделяется на еще ряд “подклассов”. Например, линейные САУ (САР) имеют различия по виду математического описания.
Поскольку в этом семестре будут рассматриваться динамические свойства только линейных систем автоматического управления (регулирования), то ниже приведем классификацию по виду математического описания для линейных САУ (САР):

1) Линейные системы автоматического управления, описываемые в переменных «вход-выход» обыкновенными дифференциальными уравнениями (ОДУ) с постоянными коэффициентами:

где x(t) – входное воздействие; y(t) – выходное воздействие (регулируемая величина).

Если использовать операторную («компактную») форму записи линейного ОДУ, то уравнение (1.4.1) можно представить в следующем виде:

где, p = d/dt — оператор дифференцирования; L(p), N(p) — соответствующие линейные дифференциальные операторы, которые равны:

2) Линейные системы автоматического управления, описываемые линейными обыкновенными дифференциальными уравнениями (ОДУ) с переменными (во времени) коэффициентами:

В общем случае такие системы можно отнести и к классу нелинейных САУ (САР).

3) Линейные системы автоматического управления, описываемые линейными разностными уравнениями:

где f(…) – линейная функция аргументов; k = 1, 2, 3… — целые числа; Δt – интервал квантования (интервал дискретизации).

Уравнение (1.4.4) можно представить в «компактной» форме записи:

Обычно такое описание линейных САУ (САР) используется в цифровых системах управления (с использованием ЭВМ).

4) Линейные системы автоматического управления с запаздыванием:

где L(p), N(p) — линейные дифференциальные операторы; τ — время запаздывания или постоянная запаздывания.

Если операторы L(p) и N(p) вырождаются (L(p) = 1; N(p) = 1), то уравнение (1.4.6) соответствует математическому описанию динамики звена идеального запаздывания:

а графическая иллюстрация его свойств привдена на рис. 1.4.1

5) Линейные системы автоматического управления, описываемые линейными дифференциальными уравнения в частных производных. Нередко такие САУ называют распределенными системами управления. ==> «Абстрактный» пример такого описания:

Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.
Если система управления представляет собой «пространственный» объект, то ==>

где зависит от времени и пространственных координат, определяемых радиусом-вектором

6) САУ, описываемые системами ОДУ, или системами разностных уравнений, или системами уравнений в частных производных ==> и так далее…

Аналогичную классификацию можно предложить и для нелинейных САУ (САР)…

Для линейных систем выполеняются следующие требования:

Статической характеристикой называется зависимость выхода от величины входного воздействия в установившемся режиме (когда все переходные процессы затухли).

Для систем, описываемых линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами статическая характеристика получается из уравнения динамики (1.4.1) приравниванием нулю всех нестационарных членов ==>

На рис.1.4.2 представлены примеры линейной и нелинейных статических характеристик систем автоматического управления (регулирования).

Нелинейность членов, содержащих производные по времени в уравнениях динамики, может возникнуть при использовании нелинейных математических операций (*, /, , , sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ

отметим, что в этом уравнении при линейной статической характеристики второе и третье слагаемые (динамические члены) в левой части уравнения — нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.

1.4.2. Классификация по характеру передаваемых сигналов

По характеру передаваемых сигналов системы автоматического управления (или регулирования) подразделяются:

Системой непрерывного действия называется такая САУ, в каждом из звеньев которой непрерывному изменению входного сигнала во времени соответствует непрерывное изменение выходного сигнала, при этом закон изменения выходного сигнала может быть произвольным. Чтобы САУ была непрерывной, необходимо, чтобы статические характеристики всех звеньев были непрерывными.

Системой релейного действия называется САУ, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторые моменты процесса управления меняется “скачком” в зависимости от величины входного сигнала. Статическая характеристика такого звена имеет точки разрыва или излома с разрывом.

Системой дискретного действия называется система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина имеет вид отдельных импульсов, появляющиеся через некоторый промежуток времени.

Звено, преобразующее непрерывный сигнал в дискретный сигнал, называется импульсным. Подобный вид передаваемых сигналов имеет место в САУ с ЭВМ или контроллером.

Наиболее часто реализуются следующие методы (алгоритмы) преобразования непрерывного входного сигнала в импульсный выходной сигнал:

На рис. 1.4.5 представлена графическая иллюстрация алгоритма амплитудно-импульсной модуляции (АИМ). В верхней части рис. представлена временная зависимость x(t) — сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис.). Длительность импульсов – одинакова и равна Δ. Амплитуда импульса на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе данного блока.

Данный метод импульсной модуляции был весьма распространен в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) в 70-х…80-х годах прошлого столетия.

На рис. 1.4.6 представлена графическая иллюстрация алгоритма широтно-импульсной модуляции (ШИМ). В верхней части рис. 1.14 представлена временная зависимость x(t) – сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования Δt (см. нижнюю часть рис. 1.14). Амплитуда всех импульсов – одинакова. Длительность импульса Δt на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе импульсного блока.

Данный метод импульсной модуляции в настоящее время является наиболее распространенным в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) и САУ других технических систем.

Завершая данный подраздел, необходимо заметить, что если характерные постоянные времени в других звеньях САУ (САР) существенно больше Δt (на порядки), то импульсная система может считаться непрерывной системой автоматического управления (при использовании как АИМ, так и ШИМ).

1.4.3. Классификация по характеру управления

По характеру процессов управления системы автоматического управления подразделяются на следующие типы:

Выходной стохастический сигнал характеризуется:

Кроме приведенных основных видов классификации систем управления, существуют и другие классификации. Например, классификация может проводиться по методу управления и основываться на взаимодействии с внешней средой и возможности адаптации САУ к изменению параметров окружающей среды. Системы делятся на два больших класса:

1) Обыкновенные (несамонастраивающиеся) СУ без адаптации; эти системы относятся к разряду простых, не изменяющих свою структуру в процессе управления. Они наиболее разработаны и широко применяются. Обыкновенные СУ подразделяются на три подкласса: разомкнутые, замкнутые и комбинированные системы управления.

2) Самонастраивающиеся (адаптивные) СУ. В этих системах при изменении внешних условий или характеристик объекта регулирования происходит автоматическое (заранее не заданное) изменение параметров управляющего устройства за счет изменения коэффициентов СУ, структуры СУ или даже введения новых элементов.

Другой пример классификации: по иерархическому признаку (одноуровневые, двухуровневые, многоуровневые).

Источник