Что называется ребрами маршрута

05. Маршруты в графе

Определение. Маршрутом В графе называется чередующаяся последовательность вершин и рёбер 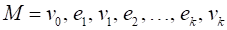, в которой любые два соседних элемента являются инцидентными.

Длиной маршрута называется число ребер в нём с учётом повторений.

Замкнутым называется маршрут, начало и конец которого находятся в одной вершине. Иначе, маршрут называется Открытым.

Цепью называется открытый маршрут с различными ребрами. Циклом называется замкнутый маршрут с различными ребрами. Простыми называются цепь и цикл с различными вершинами.

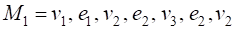
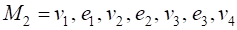
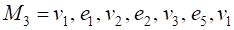
Например, в графе, диаграмма которого приведена на рис. 1, последовательность является открытым маршрутом длиной 3; последовательность является простой цепью длиной 3; последовательность является простым циклом длиной 3.

Задачи и упражнения

17. Составьте различные маршруты, содержащие четвертую вершину графа задачи 1.

18. Составьте различные маршруты длиной четыре графа задачи 1.

19. Составьте, если возможно, для графа задачи 1 следующие маршруты: открытый маршрут, но не цепь; цепь, но не простую цепь; простую цепь; замкнутый маршрут, но не цикл; цикл, но не простой цикл; простой цикл.

Источник

Виды вершин и рёбер графа. Маршруты, цепи, циклы в графах

Виды вершин и рёбер графа

Пример 1. Найти звенья в графе, представленном на рис А (под примером).

Ответ. Звенья данного графа изображены линиями 8 и 11 без указания направления.

Иначе говорят также, что в описанном случае порядок двух концов ребра графа не существенен. В случае, когда порядок, в котором указаны вершины в инциденции, существенен, соответствующее ребро называет дугой.

Пример 2. Найти дуги в графе, представленном на рис А.

Пример 3. Найти петли в графе, представленном на всё том же рис А.

Голой называют вершину, которая не инцидентна ни одному ребру графа.

Пример 4. Найти голую вершину в графе, представленном на всё том же рис А.

Изолированной называется вершина графа, которая инцидентна одной или нескольким петлям.

Две вершины a и b называются смежными, если существует по крайней мере одно соединяющее их ребро. В частности, вершина смежна сама с собой в том и только в том случае, когда при ней имеется хотя бы одна петля.

Пример 5. В графе, представленном на рис А, найти изолированные вершины, смежные и не смежные вершины, вершины, смежные сами с собой.

Кратными называются рёбра, соединяющие одну и ту же пару вершин.

Пример 6. Найти кратные рёбра в графе, представленном на всё том же рис А.

Количество рёбер, инцидентных вершине графа, называется степенью этой вершины графа.

Маршруты, цепи и циклы в графах

Маршрут, в котором все рёбра различны, называется цепью.

Цепь, в которой все вершины, кроме, возможно, первой и последней, различны, называется простой цепью.

Замкнутая цепь с положительной длиной называется циклом. Замкнутая простая цепь с положительной длиной называется простым циклом.

Пример 7. В графе, представленном на рисунке ниже, найти примеры маршрута (указать длину), любой цепи, простой цепи, цепи, не являющейся простой, любого цикла (указать длину), простого цикла (указать длину).

Ответ. В данном графе:

Граф называется связным, если существует цепь между любыми двумя его вершинами.

Источник

Учебная тема: Путь в графе

Содержание

Маршрут, цепь, цикл [ править ]

Маршрут [ править ]

Маршрутом называют последовательность вершин и ребер, в которой любые два соседних элемента инцидентны (т.е. соединены).

!В случае простого графа (графа без петель и кратных ребер) маршрут однозначно определяется последовательностью вершин или последовательностью ребер.

Длиной маршрута называют число ребер в нем с учетом повторений.

Цепь [ править ]

Цепь, в которой все вершины различны, кроме, может быть, ее концов, называется простой

Путь – это ориентированная простая цепь

Эйлеров путь (эйлерова цепь) — это путь, проходящий по всем ребрам графа и притом только по одному разу.

Цикл [ править ]

Простой цикл – это замкнутая простая цепь.

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Контур – это простой ориентированный цикл.

Расстояние между вершинами, диаметр, мост [ править ]

Расстояние между вершинами – это длина кратчайшей цепи, соединяющей эти вершины (сама такая цепь называется геодезической) рисунок

Например: расстояние между вершинами V1 и V5 это длина геодезической цепи V1-V2-V4-V5

Диаметр – это самая длинная геодезическая цепь.

Мост – это такое ребро графа, удаление которого приводит к тому, что его вершины перестают быть связными.

Например: на рисунке это ребра (2,4), (7,10), (11,12)

Точка сочленения, блок [ править ]

Точка сочленения – это вершина графа v, удаление которой из графа увеличивает число компонентов связности.

Блок – связный граф, не имеющий точек сочленения.

После удаления точки сочленения (вершины V) граф распадается на три блока

Ссылки на буклет и презентацию по данной теме [ править ]

Ресурсы [ править ]

Учебник «Дискретная математика. Курс лекций» Палий И.А.

Материал из википедии: статья «Эйлоров цикл»

Источник

Маршруты в графах

Маршрутом в произвольном графе называется чередующаяся последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной. В простом графе маршрут однозначно определяется только последовательностью вершин. Будем рассматривать следующие конечные маршруты, которые часто используются в задачах обхода графа: цепи, циклы и пути.

Для неориентированных графов справедливы следующие понятия.

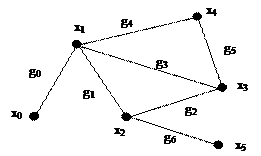Рис. 3.6. Пример цепи

Цепь называется про­стой, если все ребра в ней раз­личны, и сложной (составной) – в противном слу­чае. Вершины в простой цепи могут повторяться.

Цепь назы­вается элементарной, если в ней ни одна из вершин не повторяется.

Циклом называется конечная цепь, начинающаяся на некото­рой вершине х_i, и окачивающаяся на ней же. Простые, сложные и элементарные циклы определяются по аналогии с цепями.

Для ориентированных графов введены следующие дополни­тельные понятия.

Путем в графе G(X) называется такая последовательность дуг (g_l, g₂, …), что конец каждой предыдущей дуги является началом следующей. Существуют простые, сложные и элементар­ные пути.

Контур графа – это конечный путь, у которого начальная вер­шина совпадает с конечной. Существуют простые, слож­ные (составные) и элементарные контуры.

Длина пути есть число дуг L(s) в последовательности дуг пути s. В случае бесконечного пути L(s) = ¥.

Граф называется симметрическим, если » x_i, x_j из того, что x_i Î G(x_j) Þ x_j Î G(x_i), то есть две смеж­ные вершины x_i, x_j всегда соединены противоположно ориентирован­ными дугами (рис.3.7).

Рис. 3.7. Симметрический граф

Граф называется антисимметрическим, если » x_i, x_j
x_i Î G(x_j) Þ x_j Ï G(x_i), то есть каждая пара смежных вершин соединена только в одном направлении.

Граф называется конечным, если число его вершин конечно и бесконечным, если число вершин бесконечно. Граф G(X) называется G – конечным, если для каждой его верши­ны х Î X множество G(x) конечно.

Источник

Лекция 13. Графы

4.2. Связность

Маршруты

Определение 4.9. Последовательность из ребер графа (не обязательно различных) называется маршрутом длины , если любые два рядом стоящие в этой последовательности ребра смежные. Кроме того, если эти два рядом стоящие ребра ориентированные, то в инцидентную им вершину ребро, стоящее слева, должно входить, а ребро, стоящее справа, из нее выходить.

только из одной вершины графа.

Связные компоненты

Пусть задан неориентированный граф. Граф называется связным, если любые две несовпадающие вершины графа соединены маршрутом. Очевидно, что для связности графа необходимо и достаточно, чтобы произвольная фиксированная вершина графа соединялась маршрутом с каждой из оставшихся вершин этого графа.

Отношение связности рефлексивно (вершина всегда связана сама с собой), симметрично (из связности вершины с вершиной следует связность вершины с вершиной ) и транзитивно (если вершины , и вершины , связаны, то связаны и вершины ,). Таким образом, отношение связности для вершин есть отношение эквивалентности. Поэтому существует такое разбиение множества вершин графа на попарно непересекающиеся подмножества (классы эквивалентности), что все вершины в каждом подмножестве связаны, а вершины из различных подмножеств не связаны. Каждое такое подмножество вершин графа вместе с ребрами, инцидентными этим вершинам, образует связный подграф. Следовательно, неориентированный граф представим единственным образом в виде объединения непересекающихся связных подграфов. Эти подграфы называют связными компонентами рассматриваемого графа. Связный граф является своей единственной компонентой связности. На рис.4.21 изображен граф, который имеет три компоненты связности.

Теперь обратимся к ориентированному графу. Если в орграфе существует маршрут, связывающий вершины и , то говорят, что вершина достижима из вершины . Любая вершина считается достижимой из себя самой. Вершина орграфа называется источником, если из нее достижима любая вершина орграфа.

Связность ориентированных графов определяется в принципе так же, как и неориентированных, те есть без учета направления дуг. Специфичным для орграфа (или смешанного графа) является понятие сильной связности.

Орграф называется сильным (или сильносвязным), если любые две его вершины достижимы друг из друга. Орграф называется односторонним (или одностороннесвязным), если для любой пары его вершин, по меньшей мере, одна из них достижима из другой.

Рис.4.22 Рис.4.22 Рис.4.22

В некоторых задачах существенно требование сильной связности графа. Например, граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связанным, так как, в противном случае, нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.

Маршрут, содержащий все вершины орграфа, называется остовным.

Теорема 4.5. Орграф является сильным тогда и только тогда, когда в нем есть остовный контур, является односторонним тогда и только тогда, когда в нем есть остовный путь.

Отношение взаимной достижимости вершин орграфа рефлексивно, симметрично и транзитивно. Как отношение эквивалентности оно разбивает множество вершин орграфа на классы эквивалентности, объединяя в один класс все вершины, достижимые друг из друга. Вершины, входящие в такие классы, вместе с дугами, им инцидентными, обе концевые вершины которых принадлежат этому же классу, образуют подграфы, называемые сильными (или сильносвязнными) компонентами орграфа.

Орграф называется несвязным, когда его неориентированный дубликат не является связным графом.

Орграф, изображенный на рис. 4.25, имеет четыре сильные компоненты с множествами вершин , , , . В орграфе могут быть дуги, не входящие ни в одну из его сильных компонент, например, дуги , , и у орграфа на рис. 4. 25.

Вершинная связность и реберная связность

Сопоставляя, например, полный граф шестого порядка и его любой связный суграф, интуитивно ясно, что сам полный граф «сильнее» связан, чем его суграф. Далее речь пойдет о понятиях, характеризующих степень связности графа.

Рассмотрим граф, вершины которого соответствуют неким технологическим объектам, а ребра показывают, какие объекты могут взаимодействовать либо непосредственно друг с другом, либо опосредованно через другие объекты. Технологическая система, представленная этим графом, считается функционирующей, если каждая пара ее объектов связана между собой. В этом случае система должна иметь связный граф. Важной характеристикой системы является ее надежность (живучесть), под которой обычно понимается способность системы функционировать при выходе из строя одного или нескольких объектов и (или) нарушения связи между некоторыми из них. Очевидно, что менее надежной следует считать ту систему, которая перестает функционировать при выходе из строя меньшего количества ее элементов. Оказывается, оценить степень надежности такой системы могут помочь те понятия, о которых упоминалось чуть выше и которые сейчас будут определены.

Определение 4.10. Числом вершинной связности (или просто числом связности) графа называется число, равное наименьшему числу вершин, удаление которых приводит к несвязному или одновершинному графу.

Граф , представленный на рис. 4.26, связен, но он перестает быть связным, если удалить вершину 4. Поэтому .

Можно нарушить связность графа, удаляя некоторые его ребра (дуги). У графа (рис. 4.26) для этого придется удалить не менее трех ребер. Например, граф распадается на две компоненты после удаления ребер 4&5, 4&6, 4&7.

Определение 4.11. Числом реберной связности графа называется число, равное наименьшему числу ребер, удаление которых приводит к несвязному графу. Число реберной связности одновершинного графа полагается равным нулю.

Выше мы показали, что для графа (рис. 4.26) .

Ребро графа называется мостом, если его удаление увеличивает число компонент связности графа.

Возвращаясь к технологической системе, речь о которой шла вначале, отметим, что число вершинной связности и число реберной связности ее графа отражают чувствительность системы к повреждениям, а точки сочленения и мосты графа системы указывают на наиболее уязвимые места системы.

Граф называется неразделимым, если он связный и не имеет точек сочленения. Граф, имеющий хотя бы одну точку сочленения, является разделимым и называется сепарабельным. Он разбивается на блоки, каждый из которых представляет собой максимальный неразделимый подграф.

На рис. 4.28 показаны блоки , , графа на рис. 4.26.

Если есть минимальная степень вершин графа , то очевидно, что , поскольку удаление всех ребер, инцидентных данной вершине, приводит к увеличению числа компонент связности графа.

Теорема 4.6. Для любого графа справедливы неравенства:

.

Граф называется k-связным, если , реберно— k-связным, если .

Граф , изображенный на рис. 4.26, 1-связен и реберно-3-связен.

Источник