Что называется разверткой многогранника

Развертка поверхности многогранников

Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины отдельных граней поверхности – плоских многоугольников.

Существует три способа построения развертки многогранных поверхностей:

1. Способ нормального сечения;

3. Способ треугольника.

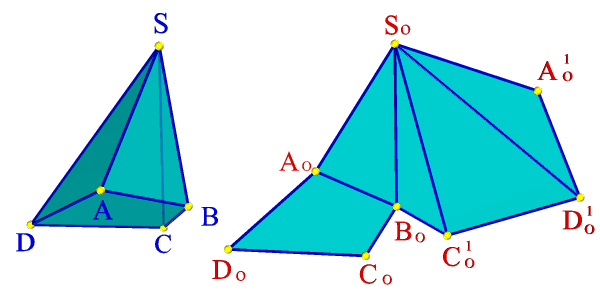
Пример 1. Развертка пирамиды (рис. 8.40).

Рисунок 8.40. Пирамида и её развертка

Рисунок 8.41. Определение истинной величины основания и ребер пирамиды

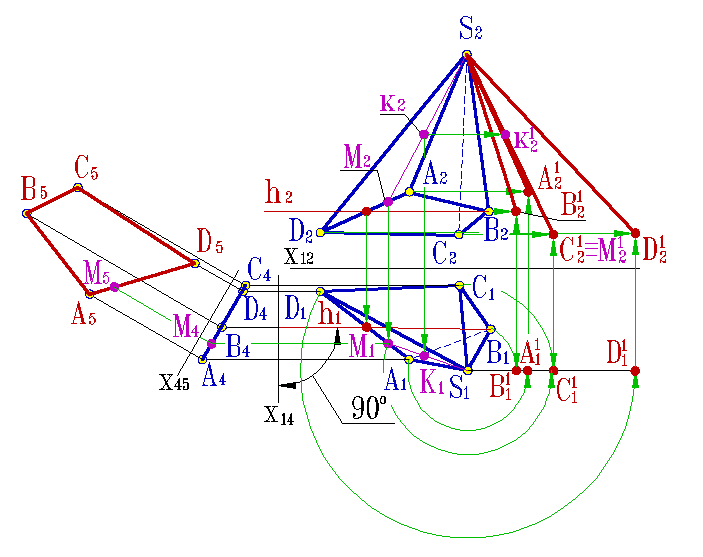
Алгоритм построения можно сформулировать следующим образом (рис. 8.41):

Определяют натуральную величину основания пирамиды (например методом замены плоскостей проекций);

Определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);

Строят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рис.8.42).

Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки.

Примером первой точки на рисунках служит точка К0 и КОSАD, а иллюстрацией второго случая являются точки М0 и М0*. Для определения точки К0 на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ ( метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S0М0 и, наконец, точки К0.

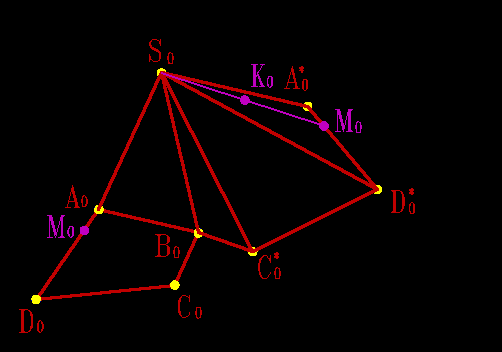
Рисунок 8.42. Построение развертки пирамиды

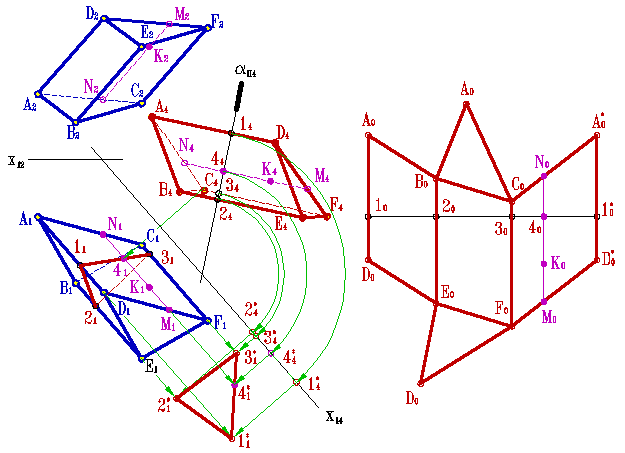
Пример 2. Развертка призмы (рис.8.43).

Рисунок 8.43. Развертка призмы способом нормального сечения

В общем случае развертка призмы выполняется следующим образом. Преобразуют эпюр так, чтобы ребра призмы стали параллельны новой плоскости проекций. Тогда на эту плоскость ребра проецируются в натуральную величину.

Пересекая призму вспомогательной плоскостью α, перпендикулярной ее боковым ребрам (способ нормального сечения), строят проекции фигуры нормального сечения – треугольника 1, 2, 3, а затем определяют истинную величину этого сечения. На примере она найдена методом вращения.

В дальнейшем строям отрезок 10-10*, равный периметру нормального сечения. Через точки 10, 20, 30 и 10* проводят прямые, перпендикулярные 10-10*, на которых откладывают соответствующие отрезки боковых ребер призмы, беря их с новой фронтальной проекции. Так, на перпендикуляре, проходящем через точку 10, отложены отрезки 10D0=14D4 и 10А0=14А4.

Соединив концы отложенных отрезков, получают развертку боковой поверхности призмы. Затем достраивают основание.

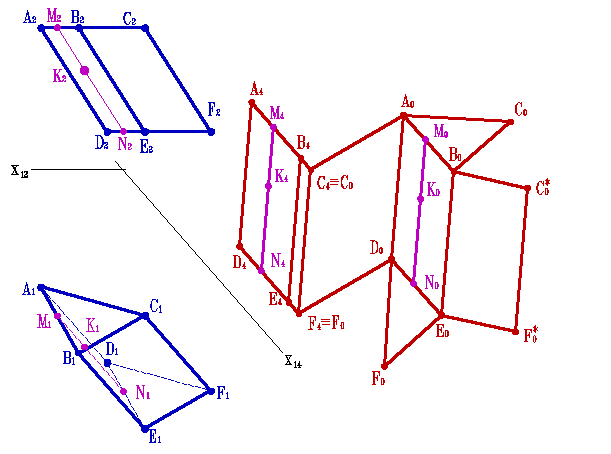
Пример 3. Развертка призмы, частный случай, когда основание призмы на одну из плоскостей проекций проецируется в натуральную величину (рис. 8.44).

Рисунок 8.44. Развертка призмы способом раскатки

Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.

Затем новую проекцию призмы вращают вокруг ребра С4F4 до тех пор пока грань ACDF не станет параллельной плоскости П4. При этом положение ребра С4F4 остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П1 то на эту плоскость проекций они проецируются без искажения т.е. R=A1C1=D1F1), расположенных в плоскостях, перпендикулярных ребру С4F4. Таким образом, траектории движения точек A и D на плоскость П4 проецируются в прямые, перпендикулярные ребру С4F4.

Когда грань ACDF станет параллельна плоскости П4, она проецируется на неё без искажения т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A4 и D4 дугой радиуса R=A1C1=D1F1, можно получить искомое положение точек развертки A0 и D0.

Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B4 и E4 делают засечки из точек A0 и D0 дугой радиуса R=A1B1=D1E1. Аналогично строится развертка последней боковой грани призмы.

Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П4 и проходящую через ребро С4F4.

Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке.

Источник

Что называется разверткой многогранника

Формальное определение развертки многогранника довольно сложное. Школьник, как правило, понимает, о чем идет речь. Развертка многогранника позволяет изящно решать многие геометрические задачи, например, находить кратчайшие расстояния между двумя точками на поверхности многогранника.
При этом необходимо рассматривать все возможные развертки. В учебнике И.Ф.Шарыгина есть дополнительный раздел, посвященный разверткам многогранников. Там приводится пример многогранника (усеченной пирамиды) и его развертки, которая перекрывает сама себя.

Математически верное определение

Совокупность многоугольников, соответственно равных граням многогранника, вместе с указанием того, какие их стороны и вершины представляют собой одни и те же ребра и вершины многогранника, называется разверткой этого многогранника.

Заданная совокупность плоских многоугольников (вместе с заданной схемой склеивания их сторон и вершин) определяет комбинаторный тип многогранника, а также форму и размеры его граней. Комбинаторный тип согласно теореме Штейница, всегда может быть реализован некоторым выпуклым многогранником, если только выполняются следующие условия:

1) должны выполняться все три требования, фигурирующие в определении многогранника;

2) число вершин, граней и ребер развертки должны удовлетворять теореме Эйлера: В+Г-Р = 2. При этом, разумеется, стороны (и вершины) многоугольников, подлежащих склейке, должны считаться одним ребром (одной вершиной) развертки).

Кроме того, для существования выпуклого многогранника с данной разверткой необходимо еще выполнение следующих метрических условий:

3) склеиваемые стороны многоугольников должны иметь одинаковую длину;

4) сумма плоских углов при каждой из вершин развертки должна быть меньше .

Если модель многогранника, изготовленную из картона, разрезать по некоторым ребрам и развернуть на плоскости, то получим многоугольник, который называют разверткой данного многогранника (эту фигуру также называют разверткой поверхности данного многогранника).

Многоугольники, составляющие развертку многогранника, называются гранями развертки, стороны этих многоугольников называются ребрами развертки, и склеиваемые стороны многоугольников считаются за одно ребро развертки. Вершины многоугольников называются вершинами развертки, и склеиваемые вершины многоугольников считаются за одну вершину развертки.

Отождествление (склеивание) вершин развертки происходит при отождествлении (склеивании) ее ребер, так как вершины являются концами ребер.

Комментарий

Пример многогранника, о котором говорится в словарной статье, приводится на стр.411.

Определения из учебников

Многоугольники, составляющие развертку многогранника, называются гранями развертки, стороны этих многоугольников называются ребрами развертки, и склеиваемые стороны многоугольников считаются за одно ребро развертки. Вершины многоугольников называются вершинами развертки, и склеиваемые вершины многоугольников считаются за одну вершину развертки.

Отождествление (склеивание) вершин развертки происходит при отождествлении (склеивании) ее ребер, так как вершины являются концами ребер.

Правило склеивания состоит в следующем:

2) каждая сторона склеивается самое большее с одной стороной другого или того же самого многоугольника;

3) от каждого многоугольника можно перейти к любому другому, переходя последовательно от одного многоугольника к другому через их склеенные стороны.

Стороны многоугольников называются ребрами развертки при условии, что склеенные стороны считаются за одно ребро. Стороны, не склеенные с другими, образуют край развертки.

Вершины многоугольников называются вершинами развертки при условии, что отождествленные вершины многоугольников считаются за одну вершину

Источник

Развёртка многогранника

Модели многогранников часто склеиваются из развёрток или отдельных многоугольников с указанием сторон, которые должны быть склеены.

Связанные понятия

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

Существует два определения хирального многогранника. По одному определению — это многогранник в прямом смысле хиральности (или «зеркальной симметричности»), то есть, что многогранник не имеет зеркальной симметрии. По этому определению многогранник, у которого отсутствует любая симметрия, вообще будет примером хирального многогранника.

В геометрии однородный многогранник — это многогранник, грани которого являются правильными многоугольниками, и он вершинно транзитивен (транзитивен относительно вершин, а также изогонален, то есть имеется движение, переводящее вершину в любую другую). Отсюда следует, что все вершины конгруэнтны, и многогранник имеет высокую степень зеркальной и вращательной симметрии.

Многогранник, многоугольник или мозаика является изотоксальным или рёберно транзитивным, если его симметрии действуют транзитивно на его рёбрах. Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.

Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Источник

Развёртывание поверхностей

Содержание:

Развертывание цилиндров и конусов основывается на способах развертки гранных поверхностей приведенных выше. В общем случае поверхность цилиндра аппроксимируется призматической поверхностью, а конус – пирамидой и затем строится приближенная развертка кривой поверхности.

Свойства развёрток

Развёрткой криволинейной поверхности Ф называется плоская фигура , полученная путём совмещения поверхности Ф с плоскостью Σ (рис. 5.1). В начертательной геометрии плоскостью Σ является одна из плоскостей проекций.

Развёртывание поверхности

Применение развёрток

Поверхности Ф, которые можно совместить с плоскостью Σ без разрывов и складок, являются, развёртывающимися. К ним принадлежат все многогранники (см. п. 4.1), цилиндрические и конические поверхности (см. п. 3.2.1.3, рис. 3.55 б – в), торсы (см. п. 3.2.1.3, рис. 3.57). Все другие кривые поверхности не развёртываются на плоскость, поэтому при их изготовлении из листового материала они приближённо заменяются развёртывающимися поверхностями (призмами, пирамидами, цилиндрами, конусами). В этих случаях имеют место так называемые условные развёртки (см. п. 5.4.1.3 – 5.4.1.4).

Основные свойства развёрток:

а) прямая l на поверхности Ф отвечает прямой на развёртке

б) параллельные прямые на поверхности Ф отвечают параллельным прямым на развёртке

в) длина (натуральная величина) любой линии s на поверхности Ф равна длине линии на развёртке

г) угол α между линиями r, s на поверхности Ф равен углу между линиями на развёртке

д) площадь S фигуры на поверхности Ф равна плоскости соответствующей фигуры на развёртке

е) если прямая на развёртке отвечает кривой линии s на поверхности Ф, то кривая s является геодезическою линией поверхности Ф. Длина дуги МN геодезической линии является наименьшей из всех возможных дуг MN на поверхности Ф.

Описанные свойства геометрически интерпретированы на рис. 5.3.

Свойства развёрток

Геодезическая линия широко применяется в неэвклидовой геометрии, теоретических и практических задачах геодезии – науки, которая изучает измерения пространства, в том числе размеры и форму Земли, её гравитационное поле и т.д.

Развёртывание поверхности многогранника

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью. Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Способ натуральных граней

Согласно свойствам развёртки (см. п. 5.1) все грани многогранника Ф сохраняют на развёртке свою длину, для определения которой используются способы начертательной геометрии.

На рис. 5.4 построены горизонтальная и фронтальная проекции треугольной пирамиды SABC. Основа АВС является плоскостью горизонтального уровня, поэтому проецируется на П1 в натуральную величину А1В1С1. Для определения натуральных величин граней SAB, SBC, SCA используется способ вращения вокруг горизонтально-проецирующей оси і, которая проходит через вершину S пирамиды. Отрезки являются натуральными величинами ребер SA, SB, SC пирамиды. По этим ребрам строится развёртка пирамиды. Вырезав плоскую заготовку из контура развёртки и сложив её по линиям сгиба и совмещая одноименные рёбра, можно получить поверхность данной пирамиды SABC.

Способ натуральных граней

Для определения на развёртке произвольной точки D пирамиды применяется способ вспомогательного отрезка. Точка D принадлежит грани SАС. Через вершину S и точку D проводится отрезок S-1, точка 1 которого принадлежит основе АВС пирамиды. Определяется натуральная величина отрезка S-1, на нём определяется проекция На отрезке развёртки строится отрезок , длина которого равна длине проекции

Способ нормального сечения

Способ нормального сечения применяется для построения развёртки призм, ребра которых являются прямыми уровня.

Суть способа нормального сечения

Призма пересекается в произвольном месте плоскостью Σ, перпендикулярной рёбрам. Определяется натуральная величина линии 1 – 2 – … нормального сечения. Эта линия является плоским многоугольником, количество сторон которого равно количеству граней призмы. Линия 1 – 2 – … разворачивается до формы прямого отрезка … На перпендикулярах, проведенных по обе стороны от точек …, строятся части натуральных величин рёбер пирамиды, которые находятся по разные стороны секущей плоскости Σ.

На рис. 5.5 заданы две проекции треугольной призмы ABCDEF с рёбрами AD, BE, CF горизонтального уровня. Вводится секущая плоскость Σ, перпендикулярная рёбрам призмы (горизонтальный след Σ1 перпендикулярен горизонтальным проекциям рёбер призмы). Плоскость Σ пересекает призму по треугольнику 1 – 2 – 3, точки которого принадлежат, соответственно, рёбрам AD, BE, CF. Способом замены плоскостей проекций определяется натуральная величина нормального сечения (ось параллельна следу Σ1). Треугольник разворачивается до формы прямого отрезка длины частей которого равны соответствующим сторонам треугольника На перпендикулярах, проведенных по обе стороны от точек строятся отрезки длины которых равны длинам проекций На развёртке достраиваются натуральные величины основ АВС, DEF призмы.

Способ нормального сечения

Для определения на развёртке произвольной точки G призмы применяется способ вспомогательных отрезков. Точка G принадлежит грани ABDE. Через точку G проводится отрезок 4 – 5, параллельный рёбрам призмы. Точка 4 принадлежит отрезку АВ, точка 5 – отрезку DE. Определяется точка 6 пересечения отрезка 4 – 5 с плоскостью Σ. Точка 6 принадлежит отрезку 1 – 2. Определяется проекция На отрезке развёртки строится отрезок , длина которого равна длине проекции Из точки развёртки призмы проводится отрезок в направлении, перпендикулярном отрезку в сторону точки Длина отрезка равна длине проекции

Способ раскатки

Способ раскатки применяется для развёртывания призмы, основа которой параллельна одной плоскости проекций, а боковые рёбра параллельны другой плоскости проекций.

Из точек 1, 2, … основы … верхней грани призмы проводятся лучи, перпендикулярные боковым рёбрам … На этих лучах строятся точки … так, что длины отрезков … равны натуральным величинам отрезков , …

На рис. 5.6 заданы две проекции треугольной призмы с основой 1 – 2 – 3 и верхней гранью горизонтального уровня и рёбрами фронтального уровня. Из фронтальных проекций проводятся лучи, перпендикулярные фронтальным проекциям На этих лучах по очереди откладываются точки так, что длины отрезков равны натуральным величинам отрезков

Способ раскатки

Для определения на развёртке произвольной точки А призмы применяется способ вспомогательного луча. Точка А принадлежит грани Через точку А проводится отрезок параллельный рёбрам призмы, точка 4 которого принадлежит отрезку 1 – 3 основы. Из проекций проводятся лучи перпендикулярные фронтальным проекциям рёбер призмы. Из точки принадлежащей отрезку развёртки, проводится отрезок параллельный отрезку до пересечения с лучом

Развёртывание поверхностей тел вращения

По развертыванию поверхности делятся на два класса: развертываемые, которые можно совместить с плоскостью без разрывов и складок, и неразвертываемые, которые невозможно совместить с плоскостью без разрывов и складок. Развертываются все многогранные поверхности, из кривых поверхностей – только линейчатые, у которых смежные образующие параллельны между собой (цилиндрические) или пересекаются по одной точке (конические).

Из всего разнообразия поверхностей тел вращения точное развёртывание осуществляется только для прямых круговых цилиндра и конуса (рис. 5.7 – 5.8).

Поверхность прямого кругового цилиндра разворачивается в прямоугольник, одна сторона которого равна длине нормального сечения (окружности диаметром d), другая – высоте h цилиндра (рис. 5.7). Развёртка цилиндра при необходимости дополняется нижней и верхней основами – окружностями диаметром d. Для определения точки А на развёртке прямого кругового цилиндра применяется способ образующей линии. Определяется угол α, и строится образующая линия на развёртке. Она размещена на расстоянии Высота точки равна высоте точки А.

Развёртка цилиндра

Поверхность прямого кругового конуса разворачивается в сектор окружности с центром в вершине S конуса. Радиус сектора равен длине l образующей линии конуса; угол φ = 180°·d/l, где d – диаметр основы конуса (рис. 5.8). Развёртка конуса при необходимости дополняется основой – окружностью диаметром d. Для определения точки А на развёртке прямого кругового конуса применяется способ образующей линии. Определяется угол α и строится образующая линия на развёртке, положение которой определяется углом β = 0,5αd/l. Точка расположена на расстоянии равном натуральной величине отрезка SA.

Развёртка конуса

Приближённое и условное развёртывание кривых поверхностей

При построении приближенных и условных разверток используют ап-проксимацию (от approximare (лат.) – приближаться) одной поверхности к другой. Аппроксимацией называют замену одной поверхности другой – аппроксимирующей, которая приближается к заданной по каким-то опре-деленным свойствам (форма, площадь, кривизна) с той или иной степенью точности.

Способ аппроксимирующих поверхностей

Развёртка любой развёртывающейся поверхности (кроме прямых круговых конуса и цилиндра) строится приближённо. Это происходит вследствие того, что при развёртывании кривой поверхности её аппроксимируют гранями вписанных многогранников(рис. 5.9).

Способ призматических поверхностей

Например, цилиндрическая поверхность условно заменяется призмой (рис. 5.9 а), коническая поверхность – пирамидой (рис. 5.9 б).

– Аппроксимация тела вращения многогранником

Для построения приближённой развёртки цилиндрической поверхности используется способ призматических поверхностей

Суть способа призматических поверхностей

В цилиндрическую поверхность вписывается призма, количество граней которой прямо влияет на точность построения развёртки цилиндра. Строится развёртка этой призмы способом нормального сечения или раскатки (см. п. 5.2.2 – 5.2.3). Через точки на развёртке призмы проводятся плавные кривые, являющиеся контуром приближённой развёртки цилиндра. При необходимости развёртка цилиндра дополняется нижней и верхней основами.

На рис. 5.10 изображен комплексный чертёж эллиптического цилиндра, поверхность которого аппроксимируется двенадцатигранной призмой. Развёртка последней строится способом раскатки. Через точки проводятся плавные кривые (синусоиды), образующие контур развёртки цилиндра. Развёртка дополняется нижней и верхней основами цилиндра.

Способ пирамидальных поверхностей

Способ пирамидальных поверхностей используется для построения развёртки боковой поверхности конуса.

Суть способа пирамидальных поверхностей

В коническую поверхность вписывается пирамида. Строится приближённая развёртка этой пирамиды способом натуральных граней (см. п. 5.2.1). Через точки на развёртке пирамиды проводится плавная кривая, являющаяся контуром развёртки конуса. По необходимости развёртка конуса дополняется его основой.

Аппроксимация (от англ. approximation – приближение) – научный метод, состоящий в замене одних объектов другими, более простыми, приближёнными к оригиналу.

Необходимо различать такие понятия, как приближённая и условная развёртка. Приближённая развёртка касается развёртывающихся поверхностей. Условная развёртка строится для поверхностей, которые не развёртываются.

Развёртка эллиптического цилиндра

На рис. 5.11 изображен комплексный чертёж эллиптического конуса, поверхность которого аппроксимируется двенадцатигранной пирамидой. Развёртка последней строится способом натуральных граней. Через точки проводится плавная кривая, которая образует контур развёртки конуса. Развёртка дополняется основой конуса.

Развёртка эллиптического конуса

Способ цилиндрических поверхностей

Для поверхностей, которые не развёртываются. в том числе нелинейчатых, строятся условные развёртки. Основные способы построения условных развёрток такие:

а) способ цилиндрических поверхностей;

б) способ конических поверхностей;

в) метод триангуляции.

Суть способа цилиндрических поверхностей

Кривая поверхность описывается совокупностью цилиндрических поверхностей, которые в дальнейшем развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.

На рис. 5.12 построена условная развёртка сферы. Вокруг её поверхности описываются шесть одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии Длины этих образующих равны длинам их горизонтальных проекций .Расстояния между образующими одинаковы и равны длине дуги SA, то есть длине фронтальной проекции Развёрткой одной из шести цилиндрических поверхностей является фигура в форме лепестка, контур которой проходит через концы образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги . Прибавляя к полученной части еще пять, строится условная развёртка сферы.

Условная развёртка сферы.

На рис. 5.13 построена условная развёртка открытого тора. Вокруг его поверхности описываются двенадцать одинаковых цилиндрических поверхностей. Одна из таких поверхностей имеет образующие линии Длины этих образующих равны длинам их фронтальных проекций Расстояния между образующими одинаковы и равны длине дуги SA, то есть, длине горизонтальной проекции S1A1. Развёрткой одной из двенадцати цилиндрических поверхностей является фигура, контур которой проходит через концы образующих линий, удалённых одна от другой на одинаковое расстояние, равное длине дуги S1A1. Прибавляя к полученной части еще одиннадцать, строится условная развёртка тора.

Условная развёртка открытого тора

Способ конических поверхностей

Способ конических поверхностей используется для построения условных развёрток закрытых тел вращения (эллипс, параболоид, эллипсоид, двуполостной гиперболоид, закрытый тор и т.д.).

Суть способа конических поверхностей

Сегменты поверхности описываются совокупностью конических поверхностей, которые развёртываются и совмещаются по точкам и линиям. Полученная развёртка является условной развёрткой кривой поверхности.

На рис. 5.14 построена условная развёртка сферы. Вокруг её поверхности описывается одна цилиндрическая и шесть конических поверхностей с разными вершинами Длины образующих линий одинаковы и равны длине проекции Углы и радиусы развёртывания конусов определяются, как описано в п. 5.3.

Условная развёртка сферы

На рис. 5.15 построена условная развёртка эллипсоида. Вокруг его поверхности описываются одна цилиндрическая и шесть конических поверхностей с разными вершинами Длины образующих линий могут быть разными и определяются по их фронтальным проекциям. Углы и радиусы развёртывания конусов определяются, как показано в п. 5.3.

Условная развёртка эллипсоида

Метод триангуляции

Метод триангуляции (от англ. triangle – треугольник) применяется для развёртывания многогранников, приближенного развёртывания цилиндрических и конических поверхностей и поверхностей с ребром поворота (торсов), а также условного развёртывания поверхностей которые не развёртываются.

Суть метода триангуляции

Кривая поверхность разбивается на треугольники с общими сторонами. Натуральные величины этих треугольников сочетаются по общим сторонам. Внешний контур полученной плоской фигуры является приближенной или условной развёрткой заданной кривой поверхности.

На рис. 5.16 построена приближённая развёртка торса Ф. Последний разбивается совокупностью треугольников с вершинами 1, 2, …, принадлежащими ребру возврата и одной из линий l поверхности Ф. Натуральные величины сторон 1 – 2, 2 – 3, … треугольников определяются способом вращения вокруг проецирующей оси. По найденным отрезкам строятся натуральные величины треугольников 1 – 2 – 3, 2 – 3 – 4, …, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой торса Ф.

Приближённая развёртка торса

На рис. 5.17 построена приближённая развёртка поверхности произвольного пространственного тела. Его поверхность разбивается на треугольники, стороны которых построены по точкам 1, 2, …, А, В, …, принадлежащим соответственно верхней и нижней основам тела. Натуральные величины сторон треугольников определяются способом вращения вокруг горизонтально-проецирующих осей, проходящих через точки В, С. По найденным отрезкам строятся натуральные величины треугольников, которые сочетаются по общим сторонам. Контур полученной плоской фигуры является приближенной развёрткой поверхности тела.

Развёртка поверхности тела методом триангуляции

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник