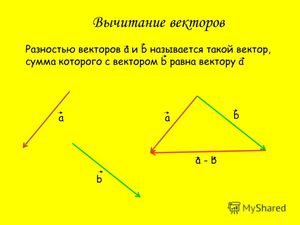
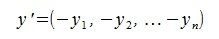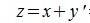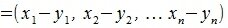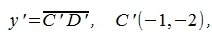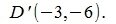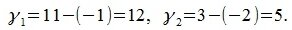Что называется разностью векторов

Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block >

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a <a₁; a₂> и b <b₁; b₂> расчёты будут иметь следующий вид: c <c₁; c₂> = <a₁ — b₁; a₂ — b₂>.

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a <a₁; a₂; a₃> и b <b₁; b₂; b₃> координаты разности будут также получены попарным вычитанием: c <c₁; c₂; c₃> = <a₁ — b₁; a₂ — b₂; a₃ — b₃>.

Вычисление разности графически

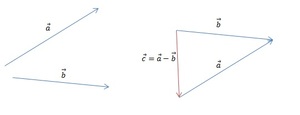
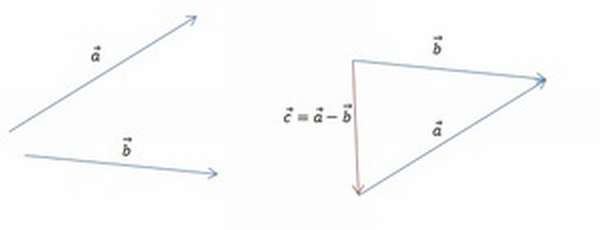
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

[block > Результат операции вычитания показан на рисунке ниже.

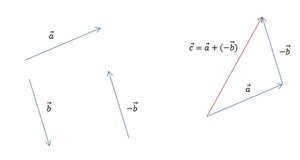
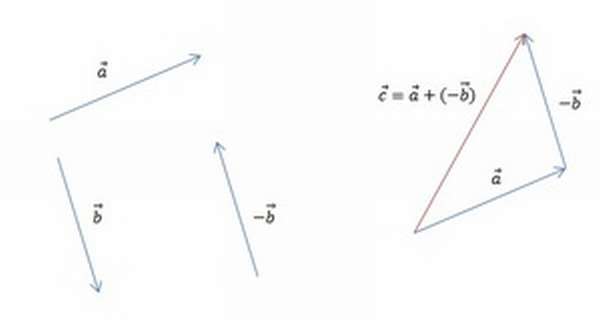
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид <c₁; c₂> = <a₁ — b₁; a₂ — b₂>. Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
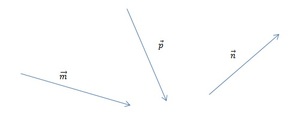
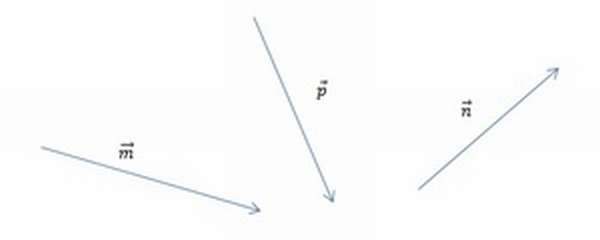
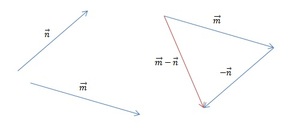
[block > Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

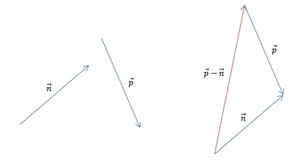
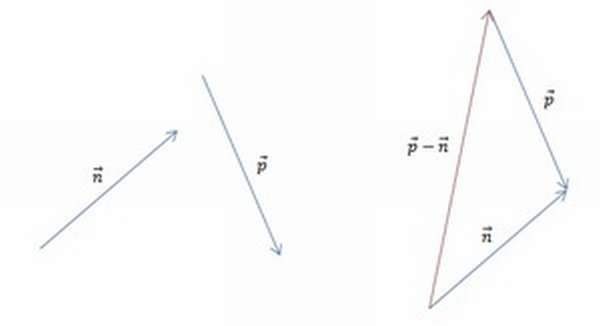
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

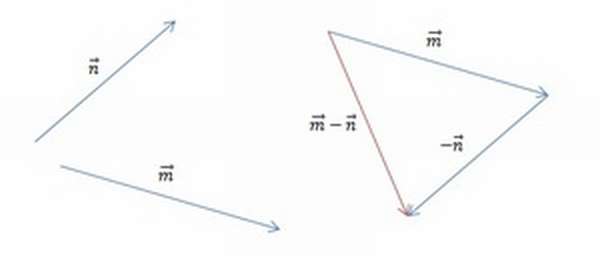
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

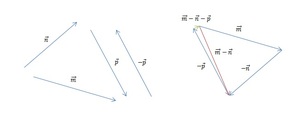
[block > Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

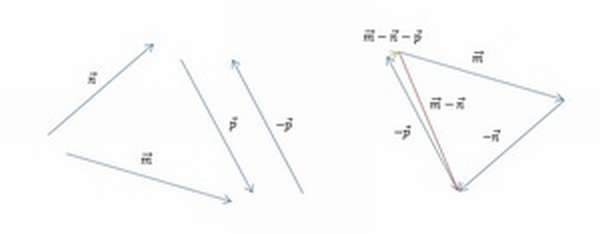
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block > [block >

Источник

Определение разности двух векторов

В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.

Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.

Определения векторной математики

Введём главные определения, используемые при выполнении линейных операций.

Аналитический метод

Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.

Для двухмерного пространства и векторных величин a и b расчёты будут иметь следующий вид: c = .

В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a и b координаты разности будут также получены попарным вычитанием: c = .

Вычисление разности графически

Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:

Результат операции вычитания показан на рисунке ниже.

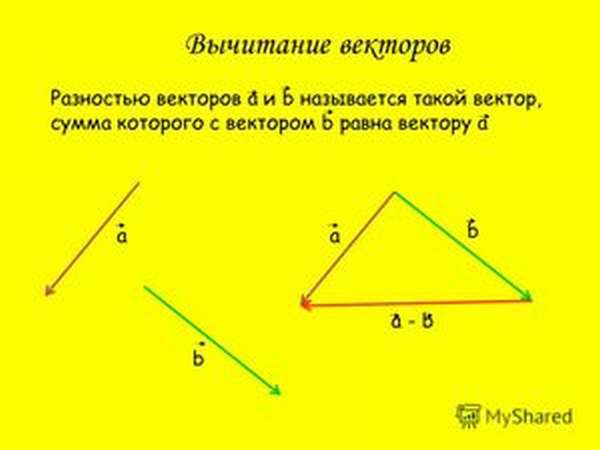
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:

Результат такого решения изображён на рисунке:

Решение задач

Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.

Задача 1. На плоскости заданы 4 точки: A (1, —3), B (0, 4), C (5, 8), D (—3, 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.

Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1, —3), а концом B (0, 4). Рассчитаем координаты направленного отрезка:

Аналогичный расчёт выполняется для CD:

Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид = . Для конкретного случая можно записать:

Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.

Задача 2. На рисунке изображены векторы m, n и p.

Необходимо построить для них разности: p — n, m — n, m — n — p. Выяснить, какая из них обладает наименьшим модулем.

Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.

Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.

Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:

Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:

Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).

Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.

Источник

Разность векторов

Разностью x-y векторов x и y называется вектор z такой, что z+y=x.

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим разность векторов и .

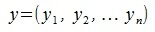
Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y’. Противоположный вектор y’ строится просто:

Из выражения (1) видно что для построения разницы векторов достаточно вычислить разницы соответствующих координатов векторов x и y.

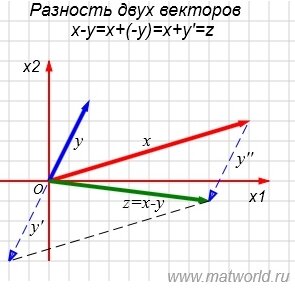
На рисунке Рис. 1 в двухмерном пространстве представлен разность векторов x=(10,3) и y=(2,4).

Вычислим z=x-y=(10-3,3-4)=(7,-1). Сравним полученный результат с геометрической интерпретацией. Действительно, после построения вектора y’ и параллельного перемещения начальной точки вектора y’ на конечную точку вектора x, получим вектор y», а после сложения векторов x и y», получим вектор z.

Вариант 2. Начальные точки векторов произвольные.

В этом случае процесс вычисления разницы векторов не так очевиден. Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y’. Здесь в качестве противоположного к вектору y можно взять тот же вектор y и поменять направление вектора, изменив начальный и коненый точки местами. Можно также взять вектор y’, который симметричен с y относительно начала координат. 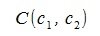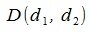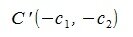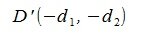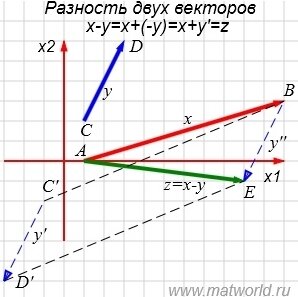Если начальный и конечный точки вектора y и , то начальный и конечный точки противоположного вектора y’ будут и соответственно. Таким образом для вычисления разницы векторов x и y, вычисляем сумму векторов x и y’ (подробно см. в разделе сложение векторов).

На рисунке Рис. 2 в двухмерном пространстве представлен разность векторов x= AB и y= CD, где A(1,0), B(11,3), C(1,2), D(3,6). Для вычисления вектора z=x-y, построен противоположный к вектору y вектор y’:

Далее нужно сложить векторы x и y’. Вектор y’ перемещается параллельно так, чтобы точка C’ совпала с точкой B. Для этого вычисляются разницы координатов точек B и С:

Источник

Сложение и вычитание векторов

Существование: Имеем два следующих случая:

Из данного выше построения сразу же будет следовать единственность данного вектора.

Сумма векторов. Сложение векторов. Правило треугольника

Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

Такая операция выполняется по правилу многоугольника.

Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
\( \vec + \vec = \left( <+ , + , + > \right) \)

Отметим несколько свойств сложения двух векторов:

Для произвольного вектора \( \overrightarrow \) выполняется равенство

Для произвольных точек \( A,\ B\ и\ C \) справедливо следующее равенство

Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов

Длина нулевого вектора равна нулю:
\( \left| \vec <0>\right| = 0 \)

Умножение вектора на число

Определение Произведением вектора \( \overrightarrow \) на действительное число \( k \) называется вектор \( \overrightarrow \) удовлетворяющий следующим условиям:

Длина вектора \( \overrightarrow \) равна \( \left|\overrightarrow\right|=\left|k\right||\overrightarrow| \) ;

Векторы \( \overrightarrow \) и \( \overrightarrow \) сонаправлены, при \( k\ge 0 \) и противоположно направлены, если \( k\le 0 \)

Источник

Линейные операции над векторами

Сложение векторов

Вычитание векторов

Пример 1.2. Для векторов, изображённых на рис. 1.6 (в конце), найти следующие суммы и разности:

Умножение вектора на число

2) векторы и коллинеарные ;

а) при умножении на единицу вектор не изменяется: ;

б) при умножении вектора на получается противоположный вектор: ;

Свойства линейных операций над векторами

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

Линейные комбинации векторов

Применяя линейные операции, можно составлять суммы векторов, умноженных на числа.

Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Отметим следующие свойства линейных комбинаций векторов:

1. Если векторы — коллинеарны, то любая их линейная комбинация им коллинеарна.

2. Если векторы — компланарны, то любая их линейная комбинация им компланарна.

Докажем, например, первое свойство. При умножении вектора на число получаем (по определению) вектор, колпинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем (по определению) вектор, параллельный той же самой прямой. Поэтому линейная комбинация двух коллинеарных векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных
векторов.

Источник