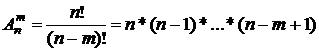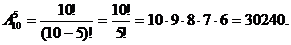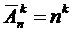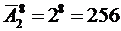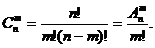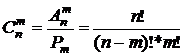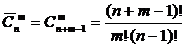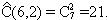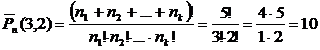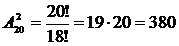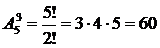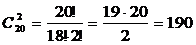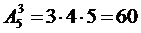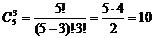Что называется размещением без повторений

10.04.202214.04.2022 admin 0 Comments

А. Размещения без повторений

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком следования.

Упорядоченные подмножества из n элементов по k элементов каждое, называются размещениями из n элементов по k элементов (или кратко: размещениями из n по k). Таким образом, размещения отличаются либо составом элементов, либо их порядком.

Пусть дано множество, состоящее из п элементов. Размещением из п элементов по к (к 4 =5!/(5-4)!=5!/1!=5×4×3×2=120.

Пример 11. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами может быть составлено расписание на 1 день?

Решение:

Пример 12. Сколькими способами можно выбрать 3 из 10 различных шаров?

B. Размещения с повторениями

Размещениями с повторениями из n элементов по k элементов называются упорядоченные множества, каждое из которых содержит k необязательно различных элементов из данного множества n элементов. Число размещений с повторениями вычисляется по формуле:

Пример 13.Сколько различных пятизначных чисел можно составить при помощи цифр 1, 2, 3?

Решение.Согласно предыдущему, искомое число равно Ā 5 ₃ =3 5 =243

Пример 14.Кодовый замок имеет на диске 12 букв. Секретное слово состоит из 5 букв. Сколько неудачных попыток можно сделать? Общее число комбинаций Ā 5 ₁₂ =12 5 =248832. Число неудачных попыток 248832-1=248831.

Пример 15. В стену здания вмонтированы 8 гнезд для флажков. В каждое гнездо вставляется либо голубой, либо красный флажок. Сколько различных случаев распределения флажков на здание.

Решение: Так как порядок расположения элементов важен и не все элементы используются в данном соединении, то это размещение. А так как всего 8 гнезд, а флажков 2 вида (голубой и красный), то они будут повторяться, т.е. это размещение с повторением.

Сочетания

A. Сочетания без повторений

Определение.Подмножества из n элементов по k элементов каждое, отличающиеся хотя бы одним элементом, называются сочетаниями из n элементов по k элементов (или кратко: сочетания из n по k). Таким образом, сочетания отличаются только составом элементов. Число сочетаний из n по k обозначается: C k _n.

Пусть дано множество, состоящее из п элементов. Сочетанием из п элементов по к (0 k _n. Так как число перестановок из к равно k!, то число размещений из п элементов по к — А k _n будет в к! раз больше, чем число сочетаний из п

Пусть имеются n различных элементов. k- сочетаниями без повторений из n элементов называют k-расстановки, составленные из этих элементов, и отличающиеся друг от друга составом, но не порядком элементов. Число k-сочетаний без повторений из n различных элементов обозначается С k _n.

Сочетаниями изn поmназываются всевозможные подмножества данных nэлементов, состоящие из m элементов. Для подсчета их числа используются следующие обозначение и формула:

Сочетанием называют комбинации, составленные из n –различных элементов по m элементов, которые отличаются только составом элементов и не зависят от порядка следования.

Пример 16. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение: Так как порядок выбранных четырех человек не имеет значения, то это можно сделать C 4 ₂₅ способами: C 4 ₂₅ = 25!/(25-4)! ×4!=12650

Пример 17. Сколькими способами можно выбрать при игре в спортлото 6 из 49 номеров?

Ответ: C 6 ₄₉=69919080

Пример 18. В кондитерской продавалось 4 вида пирожных: наполеоны, эклеры, песочные, слоеные. Сколькими способами можно купить 7 пирожных?

B. Сочетания с повторениями

Сочетанием с повторениями из m элементов по k элементов (или короче: сочетанием с повторениями из m по k) называется множество, содержащее k элементов, причем каждый элемент принадлежит к одному из m типов. Число всех вышеупомянутых сочетаний с повторениями из m по k обозначается Ĉ k _m (обратите внимание на отличие от обозначения числа сочетаний из n по k – черта сверху).Число сочетаний с повторениями из т по k равно:

Сочетания из n элементов, в каждое из которых входит m элементов, причем один и тот же элемент может повторяться в каждом сочетании любое число раз, но не более m, называются сочетаниями с повторениями. Число сочетаний с повторениями вычисляется по формуле:

Пример 19. На почте продаются открытки 10 сортов. Сколько вариантов существует для покупки 12 открыток.

Решение: Порядок расположения элементов не имеет значения, следовательно, это сочетание. А так как открытки в наборе могут повторяться, то это сочетание с повторениями.

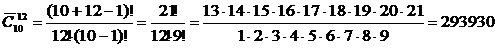
Таким образом, из 10 открыток можно выбрать набор из12 штук 293930 способами.

Пример 20.Число различных бросаний двух одинаковых кубиков равно

Пример 21.Напишем все сочетания с повторениями из трех элементов А, В, С по 3. Сколько их?

Вот они: ААА ВВВ ССС, АВВ ВСС, АСС ВВС, ААВ, ААС, АСВ. Их 10 штук, т.е.Ĉ 3 ₃.=10.

Свойства сочетаний

Все сочетания легко вычисляются, если записать их в виде треугольной таблицы (треугольника Паскаля ):

На основании данной таблицы можно увидеть справедливость указанных выше свойств сочетаний.

При определении вида комбинации удобно пользоваться схемой:

КОМБИНАТОРНЫЕ ЗАДАЧИ

Задача 1. Максимально возможное количество матчей, которое можно организовать в высшей лиге футбольного дивизиона страны не должно превышать 160 в один круг. Сколько (максимально) команд можно включить в состав высшей лиги.

n!/(n-2)!* 2!=160. Тогда n=18,4;-17,4.

Число команд должно быть натуральным числом, поэтому n = 18.

Задача 2. Имеется 4 сорта чая, 5 сортов конфет и 6 сортов печенья. Сколькими способами можно организовать чаепитие-дегустацию на трех человек, если каждый может выпить одну чашку чая определенного сорта с одной конфетой и одним печеньем?

Решение. Используя правило произведения, подсчитаем, что:

1) число способов распределить сорта чая для трех дегустаторов равно 4 3 ;

2) число способов распределить по одной конфете определенного сорта для трех дегустаторов равно 5 3 ;

Применяя еще раз правило произведения, мы получим, что число способов организовать данное чаепитие-дегустацию равно 4 3 * 5 3 * 6 3 = 1 728 000.

Задача 3. В соревнованиях принимают участие 16 команд Сколькими способами могут распределиться три первых места, т е необходимо найти число всех подмножеств, состоящих из трех элементов, отличающихся составом (номерами команд) или порядком их размещения (подмножества № 1, № 2, № 3 и № 2, № 1, № 3 являются разными). Таким образом, имеем дело с размещением. Тогда искомое число равно A 3 ₁₆=3360

Задача 4. В отделении 10 солдат. Необходимо составить наряд из 4-х человек. Сколько существует способов составления такого наряда?

Решение. Поскольку порядок, в котором мы выбираем участников наряда, не важен, то мы имеем дело с сочетаниями их 10 по 4. Итак, C 4 ₁₀=210

Задача 5. Сколько существует четырехзначных чисел, состоящих из различных цифр?

Решение. Ноль не может быть первой цифрой, следовательно, есть 9 возможностей выбрать первую цифру. Далее может следовать любая упорядоченная тройка оставшихся цифр, а для этого есть A 3 ₉ способов. Итого, получаем 9* A 3 ₉=4536

Задача 6. Сколькими способами можно раскрасить диаграмму из 4 столбцов четырехцветной ручкой так, чтобы каждый столбец был окрашен в определенный цвет.

Решение: Порядок расположения элементов имеет значение и в диаграмме 4 столбца, а ручка тоже четырехцветная, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска столбцов не повторяется (в условии сказано, что столбцы имеют разные цвета), то это перестановка без повторения. Итак, P_n = n! = 4! = 1×2×3×4 = 24 Ответ: столбцы можно закрасить 24 способами.

Задача 7. Имеется 5 кружков: 3 белых и 2 черных. Сколько различных узоров можно получить, располагая кружки в ряд.

Решение: Порядок расположения элементов имеет значение и в узоре 5 кружков, т.е. все элементы присутствуют в соединении, следовательно, это соединение – перестановка. А так как окраска кружков повторяется (в условии сказано, что 3 белых и 2 черных), то это перестановка с повторением. Итак,

Ответ: узор можно составить 10 способами.

Задача 8. Сколько словарей надо издать, чтобы можно было непосредственно выполнить перевод с любого из 5 языков на любой из 5 языков.

Решение: Порядок имеет значение (так как русско-английский и англо-русский словари различны) и не все элементы присутствуют в соединении (а только 2 из 5), значит, это размещение. Так как языки различны, то это размещение без повторения. Итак, 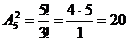. Ответ: надо составить 20 словарей.

Задача 9. На железнодорожной станции имеется 5 светофоров. Сколько может быть дано различных комбинаций их сигналов, если каждый светофор имеет 3 состояния.

Решение: Порядок имеет значение и не все элементы присутствуют в соединении, значит, это размещение. Так как цвета повторяются, то это размещение с повторением. Итак, 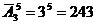. Ответ: может быть дано 243 различных комбинаций цветов.

Задача 10. 12 человек играли в городки. Сколькими способами они могут разбиться на команды по 4 человека в каждой.

Решение: Порядок расположения игроков в команде не имеет значения, следовательно, это сочетание. А так как игроки не повторяются (все члены команды различные люди), то это сочетание без повторения. Итак, .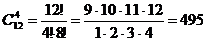

Ответ: игроки могут разбиться на команды по 4 человека в каждой 495 способами.

Задача 11. В цветочном магазине продаются цветы 6 видов. Сколько можно составить букетов из 10 цветов в каждом (букеты отличающиеся лишь расположением цветов считать одинаковыми).

Решение: Порядок расположения цветов в букете не имеет значения, следовательно, это сочетание. А так как цветы повторяются, то это сочетание с повторением. Итак, 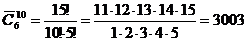. Ответ: букеты можно составить 3003 способами.

Задача 12. В группе 25 студентов, из которых 5 отличников, 11 хорошистов и остальные троечники. Сколькими способами можно выбрать группу для выполнения лабораторной работы, состоящей из 3 хорошистов, 1 отличника и 1 троечника.

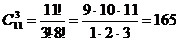
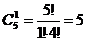
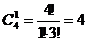
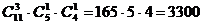
Решение: Сначала узнаем сколькими способами можно выбрать 3 хорошистов из 11 человек. Порядок расположения студентов не важен, значит, это сочетание. А так как люди в группе не повторяются, то это соединение – сочетание без повторения. Итак, одного хорошиста можно выбрать способами. Аналогично рассуждая, приходим к тому, что 1 отличника можно выбрать способами и одного троечника можно выбрать способами. Так как команда для выполнения лабораторной работы выбирается одновременно, т.е. 5 хорошистов, затем 1 отличник, затем 1 троечник, то, применив правило произведения, получим: способами. Ответ: группу для выполнения лабораторной работы можно составить 3300 способами.

Задача 13: Имеется 4 чашки, 5 блюдец, 6 ложек (все чашки, блюдца, ложки различны). Сколькими способами можно накрыть стол к чаю на 3 человека, если каждый получает 1 чашку, 1 блюдце и 1 ложку.

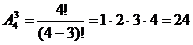
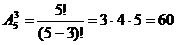
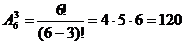
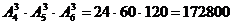
Решение: Выберем для 3 человек чашки из 4 имеющихся. Порядок расположения элементов имеет значение, и не все элементы входят в соединение, значит, это размещение. Но так чашки не повторяются, то это размещение без повторения. Итак, из 4 чашек 3 можно выбрать способами. Аналогично рассуждая, получим, что из 5 блюдец 3 можно выбрать способами, а из 6 ложек 3 можно выбрать способами. Так блюдце, чашка и ложка входят в набор одновременно, то стол можно накрыть способами. Ответ: стол можно накрыть 172800 способами.

Задача 14. Группу из 20 студентов можно разместить в аудитории по 2 человека за каждой партой. Порядок их размещения имеет значения.

Решение. Количество возможных вариантов размещений вычисляется по формуле:

Задача 15. Найти количество трехзначных чисел с неповторяющимися цифрами, которые можно составить из цифр: 1, 2, 3, 4, 5.

Решение. Количество трехзначных чисел в данном примере определяется по формуле размещений (3) и равно:

Задача 16. Группу из 20 студентов следует рассадить в аудитории по 2 человека за каждой партой. Порядок их размещения не имеет значения. Определить количество возможных вариантов сочетаний.

Решение. Количество возможных вариантов сочетаний вычисляется по формуле 4):

Задача 17. Флаг государства может комбинироваться из трёх полос разного цвета. Определить число комбинаций из пяти разных цветов, которые можно получить, выбирая из них три полосы разного цвета.

Решение. Если учитывать порядок в комбинации, то число вариантов равно:

Если же порядок в комбинации не имеет значения, то количество разных вариантов равно:

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Размещения

п.1. Размещения без повторений

Например:
Для создания 3-значного пароля используются символы из алфавита <+,*,A. 2>.
Сколько всего паролей без повторения символов можно составить?
По условию n = 5, k = 3. Рассматриваем размещение 5 символов по 3 позициям без повторений: \(\mathrm< A_5^3=\frac<5!><(5-3)!>=5\cdot 4\cdot 3 = 60 >\)
Всего 60 паролей.
Результат можно получить непосредственно из правила произведения. Действительно, на первой позиции – 5 вариантов символов, на второй – 4 оставшихся, на третьей – 3 оставшихся. Итого, по правилу произведения: 5 · 4 · 3 = 60 паролей.

п.2. Размещения с повторениями

п.3. Примеры

Пример 1. Исследуйте различие между перестановкой без повторений и размещением без повторений 〈3,2〉-выборок для трёх разноцветных фишек. Изобразите полученные решения.

Рассматриваем фишки:

1) Для перестановок, 〈3,3〉-выборок, получаем:

Что называется размещением без повторений

В каждом ряду – отдельная перестановка.
Видно, как образуется факториал. Для каждой отдельной фишки – одна перестановка. Для каждой пары фишек – две перестановки: 2 · 1. Когда добавляем третью, получаем: 3 · 2 · 1
Итого: P₃ = 3 · 2 · 1 = 6 перестановок.

2) Для размещений без повторений, 〈3,2〉-выборок, получаем:

В каждом ряду – отдельное размещение.
В первом столбце слева – 3 варианта по цвету.
Во втором столбце остается только 2 варианта.
Итого: \(\mathrm\) размещений.

Пример 2. Исследуйте перестановки без повторений и размещения для 〈4,3〉 выборок и для 〈4,2〉 выборок без повторений из 4 разноцветных фишек.
Изобразите полученные решения.

Рассматриваем фишки:

В каждом ряду – отдельная перестановка.
Итого: P₄=4·3·2·1=24 перестановки.

В каждом ряду – отдельное размещение.
Итого: \(\mathrm\) размещения.

В каждом ряду – отдельное размещение.
Итого: \(\mathrm\) размещений.

Пример 3. Исследуйте различие между перестановкой с повторениями и размещением с повторениями. Сделайте вывод.
Перестановка с повторениями: сколько слов можно получить, переставляя буквы в слове «МАМА»? Запишите все эти слова в лексикографическом порядке.
Размещение с повторениями: сколько 4-буквенных слов можно получить, используя две буквы: «М» и «А»? Запишите все эти слова в лексикографическом порядке.

1) Для перестановки с повторениями получаем: \begin \mathrm< a_1=M,k_1=2,\ \ \ a_2=A,k_2=2 >\\ \mathrm< k=k_1+k_2=2+2=4 >\\ \mathrm< P_4(2;2)=\frac<4!><2!\cdot 2!>=\frac<24><2\cdot 2>=6 > \end Все 6 слов в лексикографическом порядке:

Вывод: вариантов для размещения с повторениями получается больше, т.к. они включают слова с одной, тремя и четырьмя «М» и «А». А в перестановки с повторениями входят только слова с двумя «М» и двумя «А».

Пример 4. В базе данных с номерами телефонов содержатся все 7-значные номера.
1) Сколько в книге номеров, в которых цифры не повторяются?
2) Сколько в книге всего номеров?
3) Сколько в книге номеров, у которых 4 последних цифры одинаковые?
4) Сколько в книге номеров, у которых 4 последних цифры одинаковые, а 3 первых цифры отличаются от 4 последних?
1) Цифр – всего 10:

Источник

Перестановки, размещения и сочетания. Формулы.

Чтобы в материале было легче ориентироваться, добавлю содержание данной темы:

Введение. Множества и выборки.

В этой теме рассмотрим основные понятия комбинаторики: перестановки, сочетания и размещения. Выясним их суть и формулы, по которым можно найти их количество.

Для работы нам понадобятся кое-какие вспомогательные сведения. Начнём с такого фундаментального математического понятия как множество. Подробно понятие множества было раскрыто в теме «Понятие множества. Способы задания множеств».

Очень краткий рассказ про множества: показать\скрыть

Заметьте, что в определении выборки ничего не сказано про повторения элементов. В отличие от элементов множеств, элементы выборки могут повторяться.

Запись «n!» (читается «эн факториал») обозначает произведение всех чисел от 1 до n, т.е.

Нас же интересует общее количество этих размещений. Согласно формуле (1) количество размещений без повторений из 5 элементов по 3 будет таким:

Т.е. можно составить 60 трёхсимвольных слов, буквы которых не будут повторяться.

Следовательно, из заданных цифр можно составить 243 пятизначных числа.

В морозилке лежат пять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?

Следовательно, существует 120 порядков выбора очередности съедения.

Перестановки с повторениями

Общее количество перестановок с повторениями определяется формулой:

Следовательно, общее количество искомых слов равно 105.

В корзине размещены карточки, на которых написаны целые числа от 1 до 10. Из корзины вынимают 4 карточки и суммируют числа, написанные на них. Сколько различных наборов карточек можно вытащить из корзины?

Следовательно, общее количество искомых наборов равно 210.

Представьте себе, что мы находимся на конфетном заводе, – прямо возле конвейера, по которому движутся конфеты четырёх сортов. Мы запускаем руки в этот поток и вытаскиваем двадцать штук. Сколько всего различных «конфетных комбинаций» может оказаться в горсти?

Следовательно, общее количество искомых комбинаций равно 1771.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Алгебра и начала математического анализа. 11 класс

Конспект урока

Алгебра и начала математического анализа, 11 класс

Урок №30. Размещения без повторений.

Комбинаторика, размещения, размещения без повторений.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под редакцией Жижченко А.Б. Авторская программа «Алгебра и начала анализа 10-11 кл.», авторов

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2010.

Теоретический материал для самостоятельного изучения

Задача: Сколько различных двузначных чисел можно записать с помощью цифр 1, 2, 3, 4 при условии, что в каждой записи нет одинаковых цифр?

Перебором можно убедится, что из данных цифр можно составить 12 двузначных чисел.

В записи двузначного числа, на первом месте может стоять любая из четырех цифр, а на втором месте любая из трех оставшихся. По правилу произведения так же получаем 4*3=12.

При решении задачи, из четырех данных элементов были образованы всевозможные соединения по два элемента в каждом, причем любые два соединения отличались друг от друга либо составом элементов, либо их расположением. Такие соединения называются размещениями.

Определение: Размещениями без повторений из m элементов по n, где называются такие соединения, каждое из которых содержит n элементов, взятых из данных m разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.