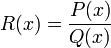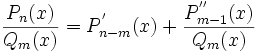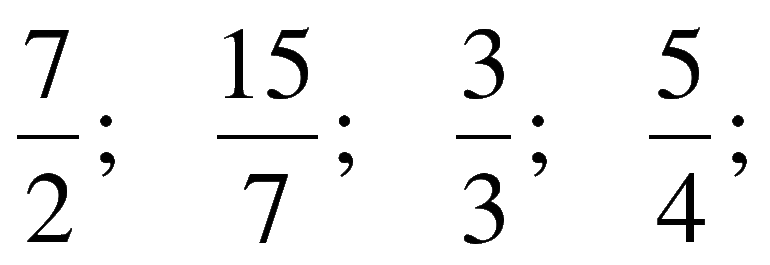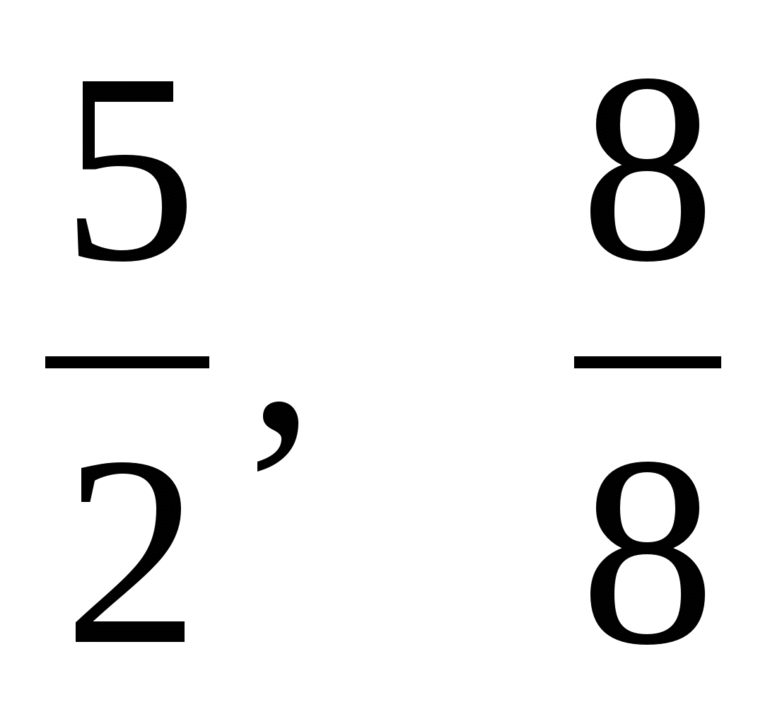Что называется рациональной дробью

Рациональная дробь

Рациональная дробь

Рациональная дробь — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид

где P(x) и Q(x) некоторые многочлены.

Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.

Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби

Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения (x − a) k (a — вещественный корень Q(x)) либо (x 2 + px + q) k (где x 2 + px + q не имеет действительных корней), причём степени k не больше кратности соответствующих корней в многочлене Q(x). На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.

См. также

Полезное

Смотреть что такое «Рациональная дробь» в других словарях:

Дробь (математика) — У этого термина существуют и другие значения, см. Дробь. 8 / 13 числитель числитель знаменатель знаменатель Две записи одной дроби Дробь в математике число, состоящее из одной или нескольких частей… … Википедия

Дробь — В Викисловаре есть статья «дробь» Наименование символа «⁄» (другое, распространённое по большей части в английском языке, название символа солидус (англ.), или слэш), например, в номерах домов. Так номер дома «5/17» читается «пять… … Википедия

РАЦИОНАЛЬНАЯ ФУНКЦИЯ — 1) Р. ф. функция w=R(z), где R(z) рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф.… … Математическая энциклопедия

РАЦИОНАЛЬНОЕ ЧИСЛО — число, выражаемое рациональной дробью. Формальная теория Р. ч. строится с помощью пар целых чисел. Р а ц и о н а л ь н о й д р о б ь ю наз. упорядоченная пара ( а, b )целых чисел а и b, у к рой b№0. Две рациональные дроби и наз. э к в и в а л е н … Математическая энциклопедия

Источник

Общие сведения

Математика — наука о числах и действиях над ними. Значение, которое можно записать в виде обыкновенной дроби, называют рациональным. Оно состоит из целого числа в числителе и натурального в знаменателе. Простое выражение можно представить как бесконечную десятичную дробь. Множество рациональных чисел обозначают латинской буквой Q. Если действительное значение не рациональное, оно иррациональное.

Выражения могут быть представлены в нестандартном виде, поэтому приходится выполнять дополнительные преобразования. Это возможно, так как делимое и делитель являются самодостаточными. Упрощения выполняются путём разложения на множители. При этом по возможности следует выполнять действия как для числителя, так и знаменателя. Операции преобразования включают в себя:

Наиболее часто вызывает сложность подбор общего знаменателя. Это приведение основывается на основном свойстве дроби. Согласно ему, умножение на ненулевой многочлен одновременно делимого и делителя не приводит к изменению результата. Отсюда следует, что числитель и знаменатель можно возводить в квадрат, извлекать корень.

Для успешного выполнения действий важно знать формулы сокращённого умножения. Это базисные знания, без которых решать рациональные дроби в 8 классе будет невозможно.

Всего используется 7 теорем: разность кубов и квадратов, произведение разности и суммы, куб суммы и разности, умножение на неполный квадрат. Используя знания, полученные в седьмом классе, многие операции можно выполнять в уме и приводить многочлен к стандартному виду без предварительного раскрытия скобок.

Свойства дроби

Пусть имеется множество, каждому члену которого поставлено в соответствие число игрек. Про такое положение говорят, что множеству задана числовая функция: y = f (x), где x Є D. Описывается область определением функции и обозначается как D (f (x)). Множество можно представить как отношение двух многочленов. Когда в числителе стоит многочлен энной степени, а в знаменателе эмной, то f (x) называют рациональным отношением или дробью.

Такие выражения обладают рядом свойств. Основное из них выражают формулой: P (x)/Q (x) = P (x) * R (x) / Q (x) * R (x). Справедливо оно лишь для случая, при котором множества Q (x) и R (x) неравны нулю, при этом R (x) является многочленом. Формулировка свойства звучит следующим образом: делимое и делитель можно помножить на одинаковое выражение. Например, им может быть число, одночлен или другой многочлен.

К другим свойствам относят:

Если равенство f/g =y/x справедливо, при этом y/x = n/m, верным будет и выражение: f/g = n/m. Отсюда следует, что рациональную дробь можно превратить в обыкновенную, если её делитель и делимое можно умножить или разделить на одинаковый многочлен. Единственное условие — он должен быть отличным от нуля.

Рациональную дробь можно представить в виде суммы. Выполняют это действие, основываясь на правиле сложения или вычитания выражений с одинаковыми знаменателями. Например, k * m — k / k+1 = 1/k + (k2 * m — k2 — k — 1) / (k2 + k).

Из свойств рациональных отношений следует, что для вычитания их друг из друга нужно привести члены к общему знаменателю и найти разность числителей. Аналогично поступают и для операции сложения, только вычитание в числителе заменяют складыванием. Произведение же находится простым перемножением делимых и делителей. А вот деление выполняют по-другому. Чтобы найти частное, нужно первое выражение умножить на обратную вторую дробь. Чтобы возвести дробь в степень, нужно отдельно в неё возвести числитель и знаменатель. По тому же принципу извлекают и корень.

Понимая, как правильно использовать приведённые свойства, решать задания на контрольной работе в школе будет несложно. Но перед сдачей теста необходимо попрактиковаться в самостоятельном решении.

Изменение знака

Следует отметить, что приём по изменению знака часто используют при разложении рациональных отношений на простейшие дроби. Например, (2×3 — 3) / (- x3 — x). Так как степень числа в числителе меньше чем в знаменателе, нужно использовать разложение. Причём в другом случае пришлось бы применять деление для нахождения целой части. Для удобства действия выражение нужно умножить на минус единицу. В результате несложно будет определить верность равенства: 2×3 + 3 / (x3 + x) = 2 + (-2x + 3) / (x3 + x).

Решение примеров

Самостоятельное решение рациональных дробей в алгебре в 8 классе строится на цепочке преобразований. Первое, что нужно сделать — оценить возможность разложения отношения на множители. Для этого лучше использовать формулы сокращённого умножения или дискриминант. Алгоритм преобразований можно представить в следующем виде:

Вот 3 типовые задачи, которые обычно предлагают решить студентам при сдаче зачёта:

При упрощении рациональных отношений сложность связана с тем, что не всегда просто найти общий множитель для числителя и знаменателя. Причём он и не всегда существует, поэтому и нужно пробовать разложение на множители. Если такого члена нет, дробь упростить нельзя.

Источник

Что называется рациональной дробью

В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения

В отличие от них выражения

помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.

Целые и дробные выражения называют рациональными выражениями.

Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.

Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла

при а = 0. При всех остальных значениях а это выражение имеет

смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Выражение вида называется, как известно, дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Примерами рациональных дробей служат дроби

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Пример 1. Найдем допустимые значения переменной в дроби

Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.

Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.

2. Основное свойство дроби. Сокращение дробей

Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство

Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.

Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :

На основании сочетательного и переместительного свойств умножения имеем:

Так как bс ≠ 0, то по определению частного

Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство

Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.

Равенство (1) выражает основное свойство рациональной дроби:

если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.

Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.

Пример 1. Приведем дробь к знаменателю

Множитель называют дополнительным множителем к числителю и знаменателю дроби

Пример 2. Приведем дробь к знаменателю

Для этого числитель и знаменатель данной дроби умножим на -1:

если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.

Пример 3. Сократим дробь

Разложим числитель и знаменатель дроби на множители:

Сократим полученную дробь на общий множитель a + 3:

Пример 4. Построим график функции

Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Рациональные дроби

Определения

Пример.

Дробь называется несократимой если ее числитель и знаменатель являются взаимно простыми полиномами.

Теорема 1. Операции сложения и умножения дробей подчиняются аксиомам коммутативности, ассоциативности и дистрибутивности.

Дробь называется правильной если степень числителя меньше степени знаменателя.

Теорема 2. Любую дробь можно представить в виде суммы полинома и правильной несократимой дроби.

Теорема 3. Сумма и произведение правильных дробей являются правильными дробями.

Разложение дроби на простейшие.

Пример. Разложить дробь

$$ \frac $$ в сумму правильных дробей.

Доказательство следует из следствия к теореме 4 и теоремы 5. ♦

Еще один способ нахождения числителей простейших дробей при разложении на них правильной дроби состоит в подборе их коэффициентов; этот метод мы проиллюстрируем в следующих пунктах.

. над множеством комплексных чисел

Пример. Разложить дробь

Пример. Разложить дробь

Пример. Разложить на простейшие дробь

. над множеством вещественных чисел

Материал этого пункта существенно используется в задаче интегрирования рациональных дробей.

Интерполяция

В отличие от полиномиальной интерполяции, не всегда имеет решение.

Производные

В настоящем пункте существенно используются результаты из раздела ОПРЕДЕЛИТЕЛЬ.

Теорема 8. Имеет место равенство:

Уничтожение иррациональности в знаменателе

Общая схема решения подобных задач ☞ ЗДЕСЬ.

Разложения в ряды.

. Тейлора

Подробное исследование этих объектов ☞ ЗДЕСЬ.

Пример. Оценить радиус сходимости ряда из предыдущего примера.

Источник

Дробные рациональные выражения

Содержание:

Дробные рациональные выражения

Дробные рациональные выражения — это выражения, составленные из чисел и переменных с использованием действий сложения, вычитания, умножения и деления на число, отличное от нуля. Дробные выражения допускают также деление на выражение с переменными. Целые и дробные выражения называют рациональными выражениями.

Рациональная дробь и ее основное свойство

Любое дробное выражение (см. п. 48) можно преобразовать к виду , где Р и Q — многочлены. Такую дробь называют рациональной дробью.

Примеры рациональных дробей:

Основное свойство дроби выражается тождеством справедливым при условиях и здесь R — целое рациональное выражение. Это значит, что числитель и знаменатель рациональной дроби можно умножить или разделить на одно и то же отличное от нуля число, одночлен или многочлен. Например,

Значит,

Например,

Сокращение рациональных дробей

Сократить дробь — это значит разделить числитель и знаменатель дроби на их общий множитель. Возможность такого сокращения обусловлена основным свойством дроби.

Для того чтобы сократить рациональную дробь, нужно числитель и знаменатель разложить на множители. Если окажется, что числитель и знаменатель имеют общие множители, то дробь можно сократить. Если общих множителей нет, то преобразование дроби посредством сокращения невозможно.

Пример:

Сократить дробь

Решение:

Имеем

Значит,

Сокращение дроби выполнено при условии

Приведение рациональных дробей к общему знаменателю

Общим знаменателем нескольких рациональных дробей называют целое рациональное выражение, которое делится на знаменатель каждой дроби (см. п. 54).

Чтобы несколько рациональных дробей привести к общему знаменателю, нужно:

1) разложить знаменатель каждой дроби на множители;

2) составить общий знаменатель, включив в произведение все множители полученных в п. 1) разложений; если некоторый множитель имеется в нескольких разложениях, то он берется с показателем степени, равным наибольшему из имеющихся;

3) найти дополнительные множители для каждой из дробей (для этого общий знаменатель делят на знаменатель дроби);

4) домножив числитель и знаменатель каждой дроби на соответствующий дополнительный множитель, привести дроби к общему знаменателю.

Пример:

Привести к общему знаменателю дроби

Решение:

Разложим знаменатели дробей на множители:

В общий знаменатель надо включить следующие множители: , а также наименьшее общее кратное чисел 12, 18, 24, т. е. К (12, 18, 24) = 72. Значит, общий знаменатель имеет вид

Дополнительные множители: для первой дроби для второй дроби для третьей дроби Значит, получаем

Сложение и вычитание рациональных дробей

Сумма двух (и вообще любого конечного числа) рациональных дробей с одинаковыми знаменателями тождественно равна дроби с тем же знаменателем и с числителем, равным сумме числителей складываемых дробей:

Аналогично обстоит дело в случае вычитания дробей с одинаковыми знаменателями:

Пример 1.

Упростить выражение

Решение:

Выполним сложение данных дробей:

Для сложения или вычитания рациональных дробей с разными знаменателями нужно прежде всего привести дроби к общему знаменателю, а затем выполнить операции над полученными дробями с одинаковыми знаменателями.

Пример 2.

Упростить выражение

Решение:

Имеем

Умножение и деление рациональных дробей

Произведение двух (и вообще любого конечного числа) рациональных дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей перемножаемых дробей:

Частное от деления двух рациональных дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй дроби:

Сформулированные правила умножения и деления распространяются и на случай умножения или деления на многочлен: достаточно записать этот многочлен в виде дроби со знаменателем 1.

Учитывая возможность сокращения рациональной дроби, полученной в результате умножения или деления рациональных дробей, обычно стремятся до выполнения этих операций разложить на множители числители и знаменатели исходных дробей.

Пример 1.

Выполнить умножение

Решение:

Использовав правило умножения дробей, получим

Пример 2.

Выполнить деление

Решение:

Использовав правило деления дробей, получим

Возведение рациональной дроби в целую степень

Чтобы возвести рациональную дробь в натуральную степень , нужно возвести в эту степень отдельно числитель и знаменатель дроби; первое выражение — числитель, а второе выражение — знаменатель результата:

Пример 1.

Преобразовать в дробь степень

Решение:

Применив правила возведения в степень дроби и одночлена, получим

При возведении дроби в целую отрицательную степень используется тождество справедливое для всех значений переменных, при которых

Пример 2.

Преобразовать в дробь выражение

Решение:

Преобразование рациональных выражений

Преобразование любого рационального выражения сводится к сложению, вычитанию, умножению и делению рациональных дробей, а также к возведению дроби в натуральную степень. Всякое рациональное выражение можно преобразовать в дробь, числитель и знаменатель которой — целые выражения; в этом, как правило, состоит цель тождественных преобразований рациональных выражений.

Пример:

Решение:

Выполняя действия с рациональными дробями, получим:

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник