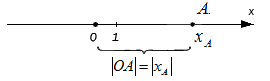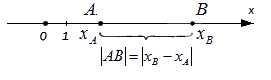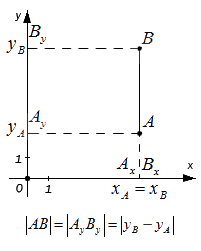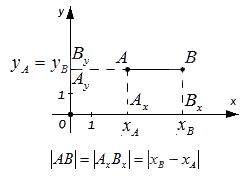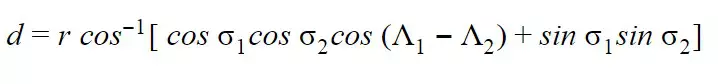Что называется расстоянием между двумя
Расстояние между двумя параллельными прямыми: определение и примеры нахождения
В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.
Расстояние между двумя параллельными прямыми: определение
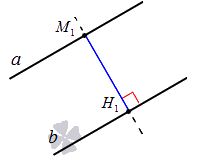
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.
Приведем иллюстрацию для наглядности:
Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.
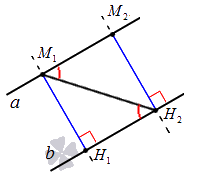
Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.
Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.
Нахождение расстояния между параллельными прямыми
Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.
Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:
— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.
Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.
Выведем эту формулу.
A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0
При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:
Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2
Разберем теорию на примерах.
Решение
Решение
Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.
Решение
Вычислим векторное произведение векторов :
Применим формулу расчета расстояния от точки до прямой в пространстве:
Что называется расстоянием между двумя прямыми?
Теорема об общем перпендикуляре двух скрещивающихся прямыхфакт
Математически верная формулировка
Расстояние между двумя скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проходящими через эти прямые.
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
Е. В. Потоскуев, Л. И. Звавич. Геометрия 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики [ПотоскуевЗвавич10у]
Формулировки из учебников
А. В. Погорелов. Геометрия: Учебник для 10 – 11 классов общеобразовательных учреждений [Погорелов10-11]
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром параллельных плоскостей, проходящих через эти прямые.
В. М. Клопский, З. А. Скопец, М. И. Ягодовский. Геометрия. Учебное пособие для 9 и 10 классов средней школы [КлопскийСкопецЯгодовский9-10]
Стандартной формулировки этой теоремы нет, но в основном тексте учебника (параграф 35) решается следующая задача:
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
На стр. 41 есть следующее замечание:
Расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.
А. Д. Александров, А. Л. Вернер, В. И. Рыжик. Геометрия: учебник для 10-11 классов общеобразовательных учреждений [АлександровВернерРыжик10-11]
Расстояние между скрещивающимися прямыми по определению учебника есть расстояние между ближайшими точками этих прямых. На стр. 100 доказывается, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
Существование и единственность общего перпендикуляра скрещивающихся прямых в учебнике не доказывается.
Расстояние от точки до точки: формулы, примеры, решения
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
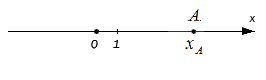
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой О А отрезки – единицы длины, мы можем определить длину отрезка O A по итоговому количеству отложенных единичных отрезков.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой x A : O A = x A
Расстояние между точками на плоскости
— если точки А и В совпадают, то расстояние между ними равно нулю;
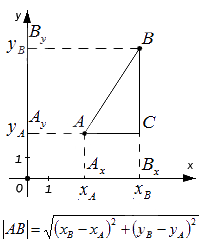
— если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
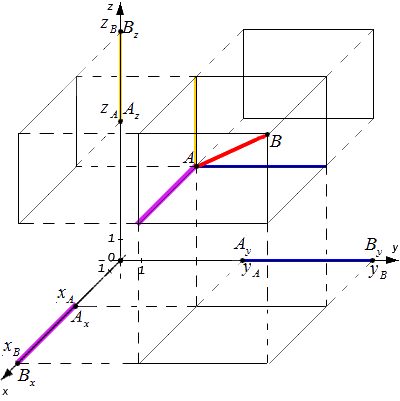
Расстояние между точками в пространстве
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: A B 2 = A x B x 2 + A y B y 2 + A z B z 2
Используя полученные ранее выводы, запишем следующее:
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
Полученная формула действительна также для случаев, когда:
— лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Решение
Решение
А также используем имеющееся условие, что А В = 5 и тогда будет верным равенство:
λ 2 + 16 = 5 λ 2 + 16 = 25 λ = ± 3
Решение
Какое расстояние между двумя точками?
Что означает расстояние между двумя точками? Расстояние между двумя точками определяется как длина прямой, соединяющей эти точки в координатной плоскости. Это расстояние никогда не может быть отрицательным, поэтому мы берем абсолютное значение при нахождении расстояния между двумя заданными точками.
Кроме того, какова формула расстояния и средней точки?
Чтобы вычислить расстояние d отрезка прямой с конечными точками (x1, y1) и (x2, y2), используйте формулу д (х2 х1) 2 (у2 у1) 2. Чтобы вычислить среднюю точку отрезка прямой с конечными точками (x1, y1) и (x2, y2), используйте формулу,. Заменять.
При этом, какое кратчайшее расстояние между двумя точками?
Также знать Какое расстояние между точками A и B 0 C? Расстояние. Следовательно, расстояние = 2c единицы.
Какая формула исчисления времени?
Чтобы найти время, используйте формулу для времени, т = д / с что означает, что время равно расстоянию, разделенному на скорость.
Что такое уравнение круга?
Как называется расстояние по прямой между двумя точками?
которая представляет собой прямую линию. Теперь убедитесь, что длина дуги действительно прямое расстояние между точками.
Как найти расстояние от одного места до другого?
Измерьте расстояние между точками
Каково расстояние между точками aa 0 и B 0?
Какое расстояние между A и C?
Каковы координаты C и D соответственно?
Как считать минуты?
Чтобы преобразовать час в минуту, умножьте время на коэффициент преобразования. Время в минуты равны часам, умноженным на 60.
Какая формула времени с примером?
Формула для времени дается как [Время = Расстояние ÷ Скорость]. Для расчета скорости формула времени будет иметь вид [Скорость = Пройденное расстояние ÷ Время].
Какая формула высоты?
Какая стандартная форма круга?
Как считать раунд?
Чтобы найти длину окружности, просто умножьте диаметр на пи (3.14). Например: если d = 23 см, C = 3.14 x 23 см, поэтому C = 72.22 см. Эта формула верна? C = pi * d вычисляет длину окружности (расстояние по внешней стороне круга).
Что такое π?
Какая формула расчета расстояния?
Узнайте, как найти расстояние между двумя точками с помощью формула расстояния, который является приложением теоремы Пифагора. Мы можем переписать теорему Пифагора как d = √ ((x_2-x_1) ² + (y_2-y_1) ²), чтобы найти расстояние между любыми двумя точками.
Как далеко клик?
Как я могу отследить пройденное расстояние?
1. MapMyWalk GPS для iPhone, Android или Windows. MapMyWalk позволяет вам видеть время, потраченное на ходьбу, расстояние, темп, скорость, высоту и сожженные калории. Когда вы закончите, MapMyWalk позволяет загружать и сохранять данные о тренировках и просматривать их как в приложении, так и на веб-сайте MapMyWalk.
Какое расстояние между точкой А и точкой Б?
Какое расстояние между точками 7 8?
Расстояние между двумя точками равно 17 единиц.
Какое расстояние между точками (- 6 2 и 8/10 на координатной сетке?
Ответ: Расстояние 2√65.
Какое расстояние между точками C и D?
Расстояние между точками C и D равно 5.
Нет, прямая линия не всегда является самым коротким расстоянием между двумя точками. Наименьшее расстояние между двумя точками зависит от геометрии объекта/поверхности. Для плоских поверхностей линия действительно является кратчайшим расстоянием, но для сферических поверхностей, таких как Земля, расстояния по большому кругу на самом деле представляют собой самое короткое расстояние.
Как оказалось, это утверждение лишь отчасти правдиво. Самое короткое расстояние между двумя точками на самом деле зависит от геометрии рассматриваемого объекта.
Большое расстояние круга
Большое расстояние круга не новая концепция; на самом деле, многие из вас уже видели это в действии.
Люди, которые путешествовали по воздуху или только проверяли маршруты полета, вероятно, заметили, что рейсы не следуют прямым путем, а вместо этого берут изогнутый маршрут к месту назначения. Изогнутые маршруты не используются для того, чтобы выкопать более глубокую яму в карманах пассажиров, а используются потому, что на самом деле они являются самым коротким расстоянием между любыми двумя заданными точками на нашей планете.
Эти изогнутые маршруты часто сбивают с толку, так как маршруты очерчены на плоской двухмерной карте, где прямая линия может показаться наименьшим расстоянием. Однако ни одна двумерная карта Земли не является точной.
Чтобы дать вам понять суть, наша любимая Земля является трехмерным пространством и лучше всего представлена с помощью модели глобуса. Однако, когда пытаешься сравнять сферу с прямоугольной формой, как это делают большинство карт, на первый план выходит вековая дилемма искажений. Большинство прямоугольных карт торгуют формами страны, размерами, промежуточными расстояниями и даже легитимной информацией для удобства понимания.
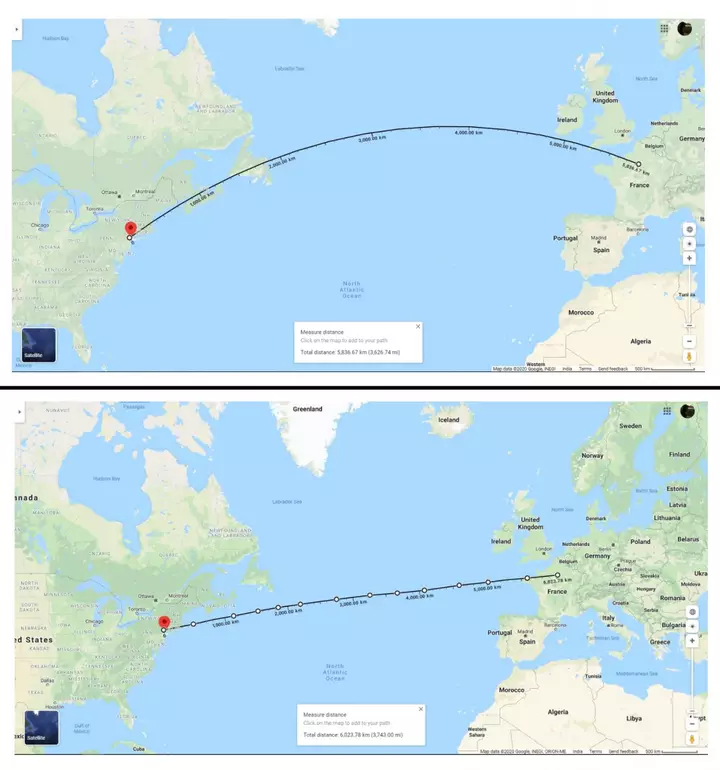
Представьте, что вы хотите улететь из кишащих крысами глубин Нью-Йорка в город любви, Париж. На глобусе кратчайшее расстояние между двумя городами было бы дугой примерно 3630 миль, но та же самая дуга, когда она проецируется на 2D-карту, превращается в прямую линию, измеряющую приблизительно 3750 миль.
Чтобы убедиться в этом самим, откройте Google Maps на соседней вкладке и найдите Нью-Йорк. Найдя его, щелкните правой кнопкой мыши на именном теге и выберите «измерить расстояние». Затем уменьшите масштаб или прокрутите немного вправо, чтобы найти Париж, и нажмите на него. Следующее расстояние будет представлять собой кривую, представляющую собой кратчайшее расстояние между двумя городами. Нажмите в любом месте на этой кривой, чтобы сделать ключевую фигуру, и перетащите её немного на юг, чтобы преобразовать кривую в прямую линию. Вы можете использовать несколько ключевых кадров, чтобы составить прямую линию между двумя точками. После этого сравните размеры кривой и прямой линии (и приготовьтесь к тому, что ваша реальность будет разрушена!).
Разница между двумя числами (3,750 – 3,630 = 120 миль) может показаться несущественной, но, учитывая тот факт, что Boeing 747 потребляет в среднем 5 галлонов топлива на милю полета, самолет потребует дополнительных (5 галлонов/км × 120 миль =) 600 галлонов (2250 литров), чтобы пройти дополнительное расстояние, что является большим делом и добавит к стоимости билетов на самолет.
Расстояние большого круга в математических терминах
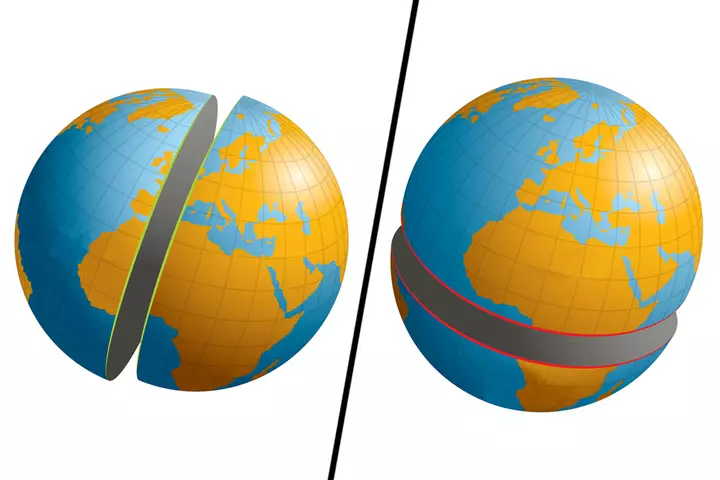
Представьте себе (или просто посмотрите на рисунок ниже), разрезая землю вдоль экватора или полюсов. Результирующие полушария в обоих случаях будут равны, и грани этих полушарий будут иметь тот же диаметр и центр, что и сама сфера (Земля).
Для любых двух не диаметральных точек (положений) на сфере (Земле) существует только один уникальный большой круг, тогда как для диаметральных точек на сфере можно нарисовать бесконечное число больших кругов. Эти точки делят окружность на две дуги; меньшая дуга представляет собой истинное кратчайшее расстояние между двумя точками и называется расстоянием большого круга.
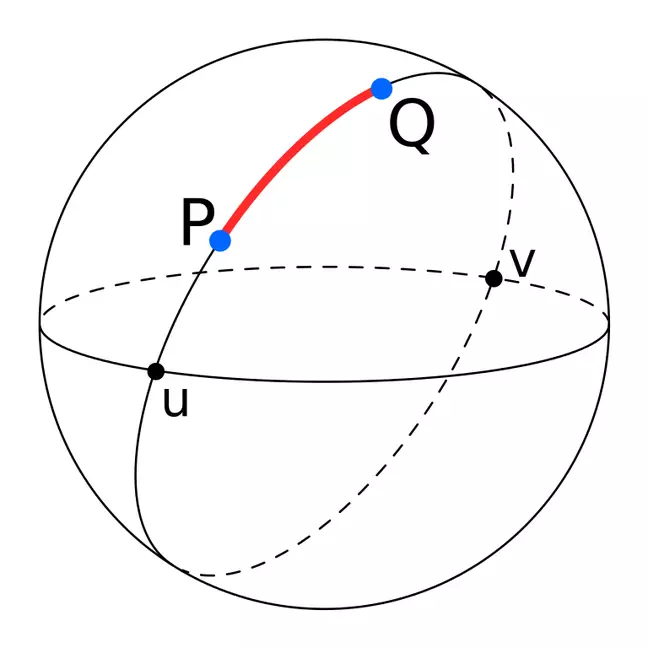
На приведенном ниже изображении точки P и Q являются двумя не диаметральными точками, а дуга PQ представляет собой кратчайшее расстояние между ними (расстояние большого круга). Точки u и v, с другой стороны, известны как противоположные или диаметрально противоположные точки и разделяют большой круг на две идентичные дуги.
Вычисление расстояния большого круга между любыми двумя точками на поверхности сферы требует использования сферической тригонометрии, и хотя мы, возможно, не были знакомы с существованием больших расстояний круга еще в наши школьные годы, всеобщая ненависть к синусам и косинусам хорошо известна.
Как уже говорилось ранее, большие круги находят свое основное применение в дальних путешествиях, в частности в воздушной и морской навигации. Искривленный характер больших окружных расстояний, дополненный вращением нашей планеты, заставляет пилотов и моряков постоянно корректировать свой курс. Поэтому большое расстояние по окружности разбивается на «линии Румба», которые представляют собой постоянное направление.
Сказав все это, даже большие расстояния по кругу не представляют собой истинное кратчайшее расстояние между двумя заданными местоположениями. Расстояния большого круга рассчитываются исходя из предположения, что Земля является идеальной сферой, но планета представляет собой более плоскую сферу с различными значениями радиуса в направлении экватора и полюсов. Значения большого круга, таким образом, имеют допуск около ± 5%.
Тем не менее большие расстояния по окружности сыграли огромную роль в дальних поездках за последние несколько лет и будут продолжать делать это, экономя топливо авиакомпаний и экономя деньги путешественников!