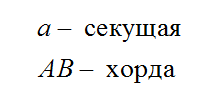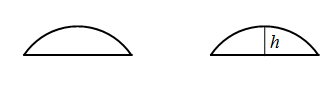Что называется радиусом окружности диаметром окружности
Окружность
Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.
Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:
Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:
Построение окружности циркулем
Для построения окружности используют специальный прибор — циркуль:
Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:
Радиус, хорда и диаметр
Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:
Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.
Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.
Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:
Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:
Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:
Для обозначения дуг используется символ 
О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.
Хорда AB стягивает дуги 

Окружность
Окружность — это геометрическая фигура, которая состоит из
всех точек плоскости, расположенных на заданном расстоянии
от данной точки.
Для решения задач, связанных с окружность, нужно знать её свойства.
Свойства окружности, как и любой другой фигуры зависят от
формы, размеров и так далее. В этой статье мы расскажем вам о
свойства окружности и об основных терминах,
таких как: хорда, радиус, дуга и так далее.
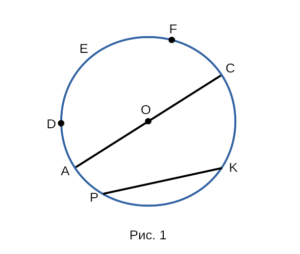
На рисунке 1 изображена окружность, где O — центр окружности,
PK — хорда, AO — радиус, АС — диаметр, DEF — дуга.
Центром окружности называется точка откуда берет начало радиус.
Расположена эта точка в центре окружности. Если внутри окружности
точка расположена на равном расстоянии от всех точек плоскости,
значит это центр окружности. O — центр окружности.
Отрезком соединяющим центр окружности и любую из точек плоскости
называют радиусом. Если отрезок внутри окружности соединяет центр
окружности с любой из точек плоскости, значит этот отрезок — радиус.
CO — радиус.
Отрезок, который соединяет две точки окружности, называется хордой.
Если отрезок внутри окружности соединяет любые две точки окружности,
значит этот отрезок — хорда. PK — хорда.
Отрезок, соединяющий две любые точки окружности и проходящий через
центр окружности, называется диаметром. Если отрезок внутри окружности
соединяет любые две точки окружности и проходит через центр окружности,
значит этот отрезок диаметр. Диаметр в два раза больше радиуса. AC — диаметр.
У диаметра есть середина, которая является центром окружности. Две любые
точки окружности делят окружность на две части. Каждая из частей называется
дугой окружности.
Если две любые точки окружности, делят её на две части,
значит эти части — дуги. DEF — дуга.
Для того, чтобы изобразить окружность на чертеже используют циркуль.
Чтобы провести окружность на местности, можно воспользоваться веревкой.
Кругом называется часть плоскости, которая ограничена окружностью.
Если часть плоскости ограничивает окружность, значит эта часть плоскости — круг.
Сумма углов окружности равна 360°.
Что называется радиусом окружности диаметром окружности
Равные отрезки, соединяющие центр с точками окружности, называются радиусами.
Хорда, дуга, диаметр
Часть окружности называется дугой.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
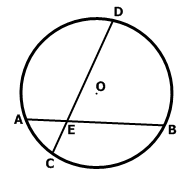
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Касательная к окружности
Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Обратная теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Определение сегмента, сектора*
Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.
Перпендикуляр, проведенный из середины хорды до пересечения с дугой называется стрелкой дуги. Длина стрелки называется высотой сегмента.
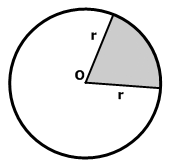
Сектором называется часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги.
Что такое окружность: определение, свойства, формулы
В данной публикации мы рассмотрим определение и свойства одного из основных геометрических объектов – окружности. Также приведем формулы, с помощью которых можно найти ее радиус, диаметр и длину.
Определение окружности
Окружность – это замкнутая кривая на плоскости, состоящая из точек, равноудаленных от определенной точки. Данная точка называется центром окружности.
Радиус окружности (R) – это отрезок, соединяющий любую точку, лежащую на окружности, с ее центром.
Диаметр окружности (d) – это линия (хорда), проходящая через центр окружности и соединяющая две противоположные точки, лежащие на ней.
Примечание: Не стоит путать окружность с кругом, т.к. круг – это множество точек плоскости, ограниченных окружностью (т.е. лежащих внутри окружности).
Свойства окружности
Свойство 1
Через три точки на плоскости, не лежащие на одной прямой, можно провести окружность, причем только одну.
Свойство 2
Точка касания двух окружностей (C) лежит на одной прямой (AB), которая проходит через их центры.
Свойство 3
Изопериметрическое неравенство: Из всех замкнутых кривых одинаковой длины окружность ограничивает область с самой большой площадью.
Формулы
1. Диаметр окружности (d):
Всё про окружность и круг
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.