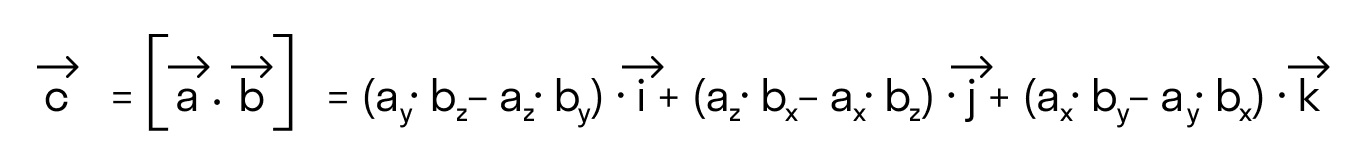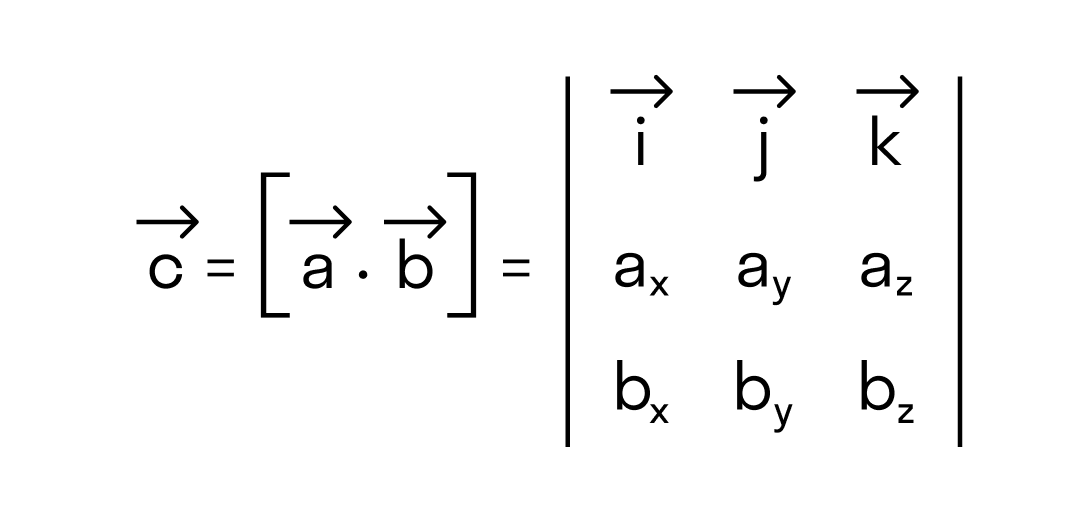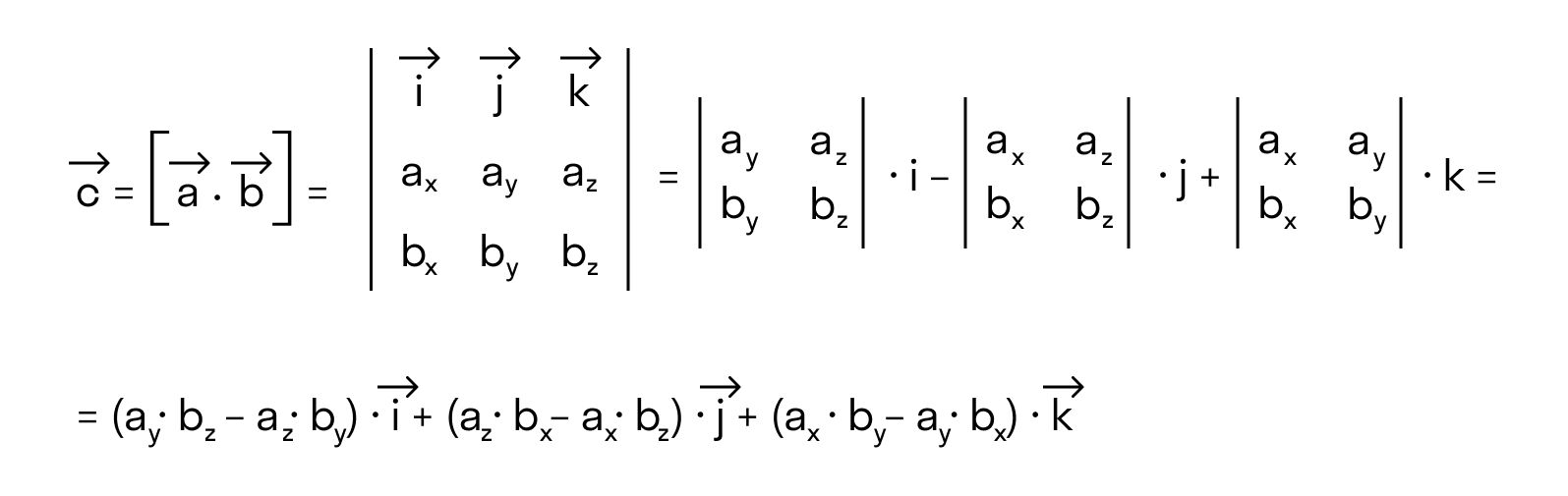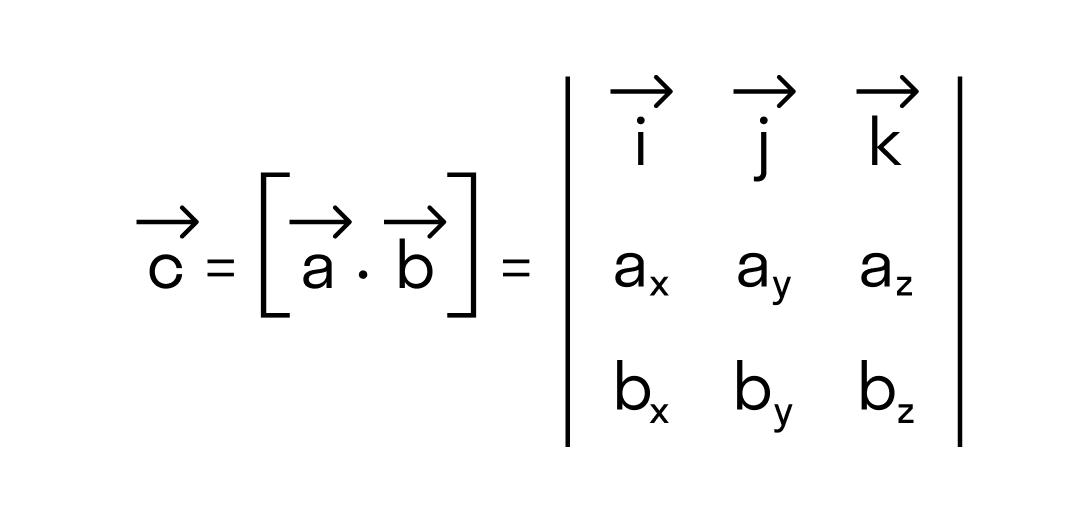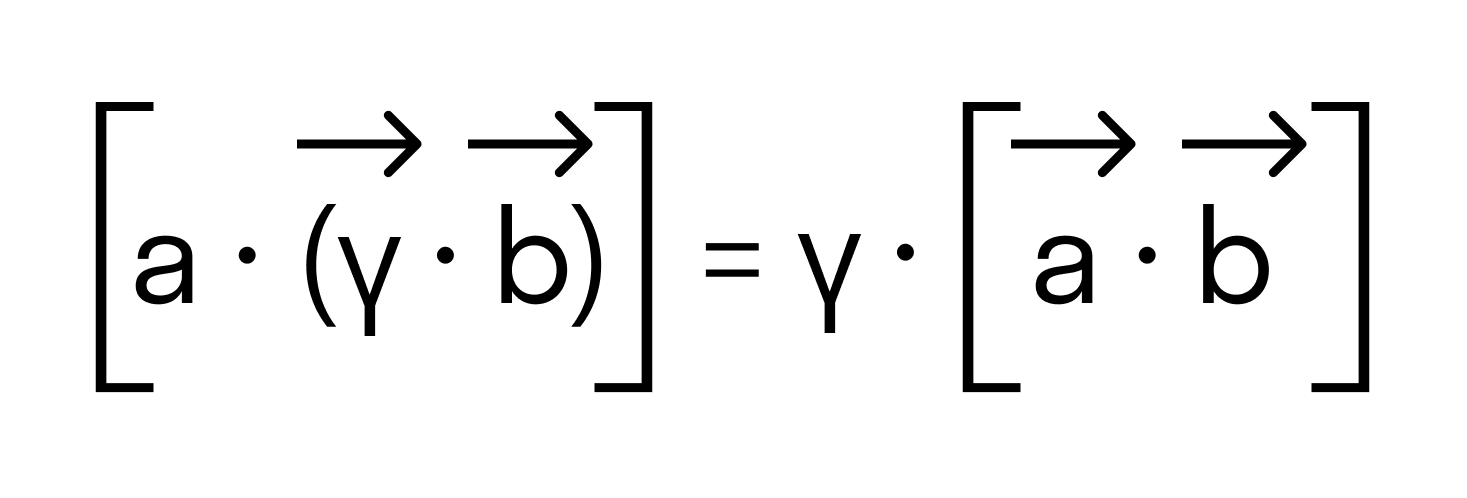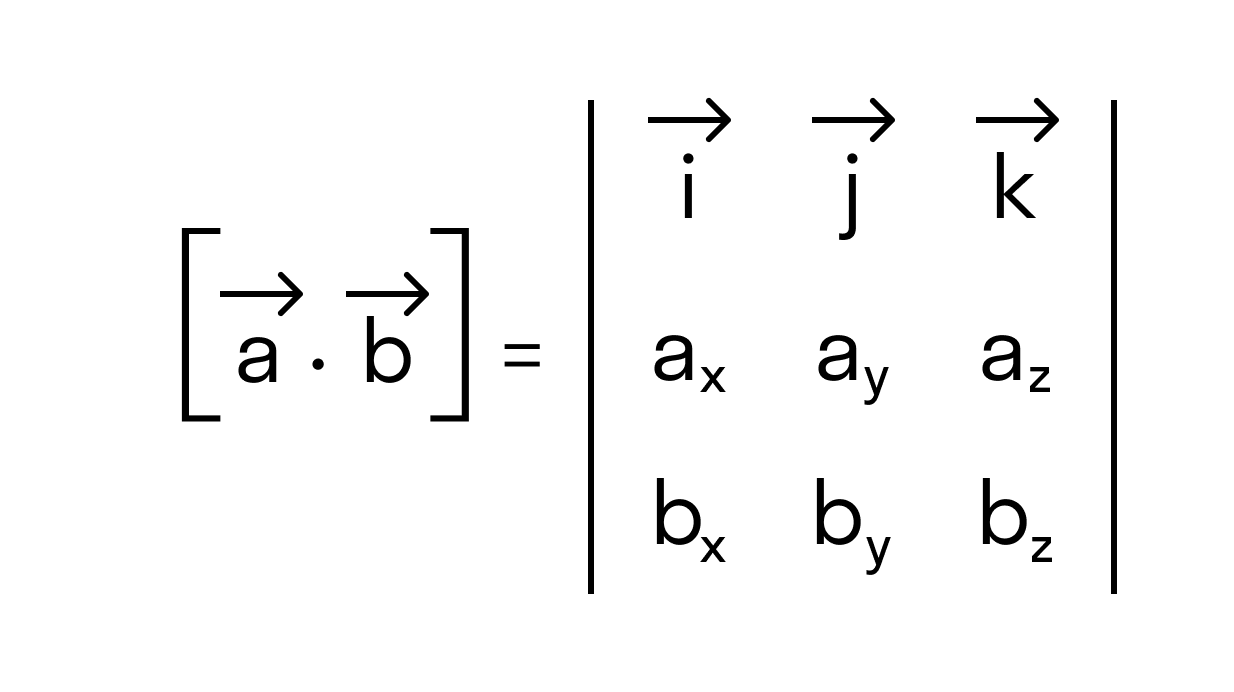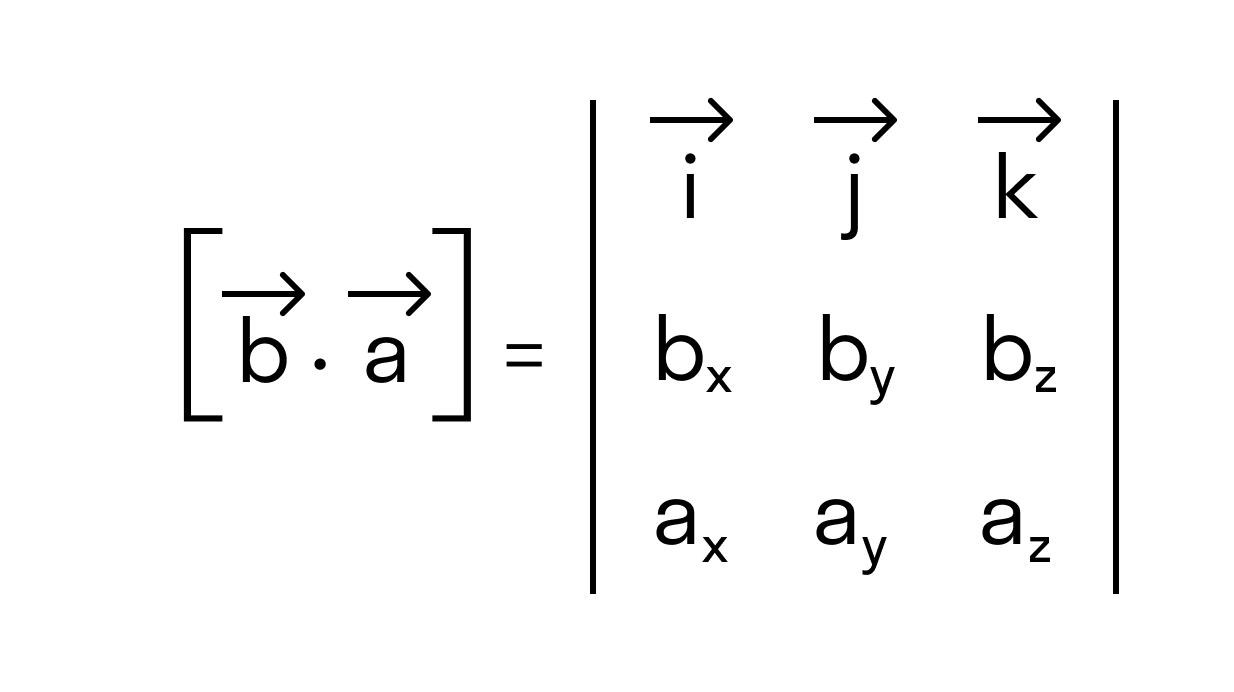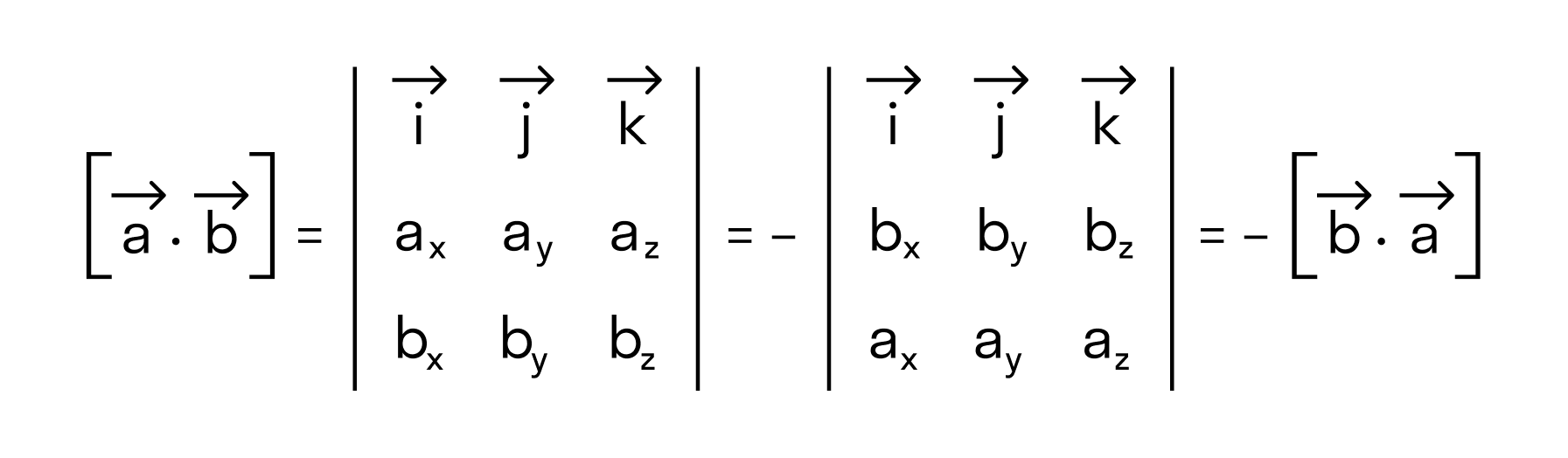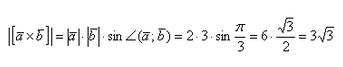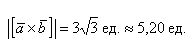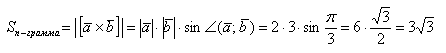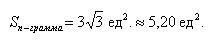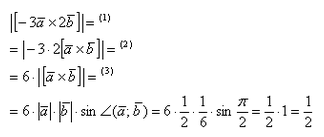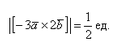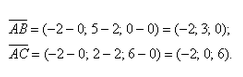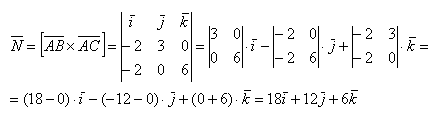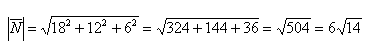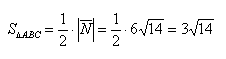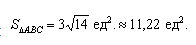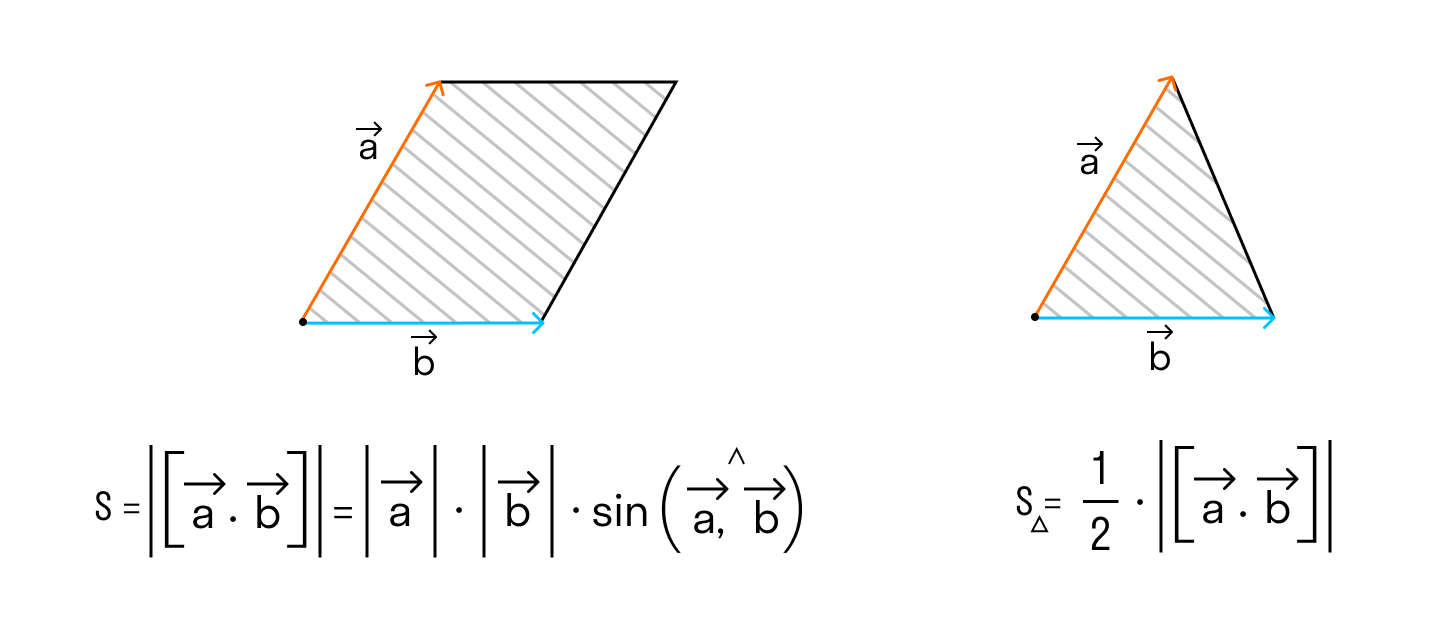Что называется произведением векторов
Определение векторного произведения
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов a → и b → будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Свойства векторного произведения
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a → = ( a x ; a y ; a z ) и b → = ( b x ; b y ; b z ) .
Рассмотрим следующие примеры.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Геометрический смысл векторного произведения
Это и есть геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Векторное произведение векторов и его свойства
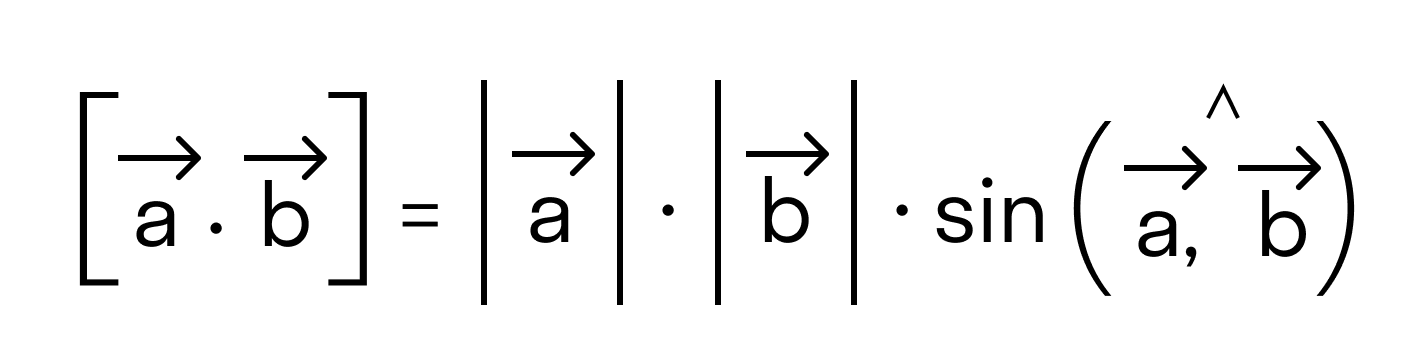
1) его длина равна произведению длин векторов и на синус угла между ними: (рис.1.42);
2) вектор ортогонален векторам и ;
Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Векторное произведение обозначается (или ).
Алгебраические свойства векторного произведения
Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство «противоположно» закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.
1. Свойства аддитивности и однородности векторного произведения означают линейность векторного произведения по первому множителю:
2. В силу антисимметричности векторное произведение линейно и по второму множителю, т.е. линейно по любому множителю.
Геометрические свойства векторного произведения
1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
Решение. Используя алгебраические свойства, найдем сначала векторное произведение
Выражение векторного произведения через координаты векторов
Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).
Найдем выражение векторного произведения через координаты множителей. Пусть в стандартном базисе векторы и имеют координаты и соответственно. Тогда, используя линейность векторного произведения по любому множителю (см. пункт 2 замечаний 1.12) и формулы (1.14), получаем
Запишем это равенство при помощи определителей второго порядка:
Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке
Формула вычисления векторного произведения
Теорема 1.8 (формула вычисления векторного произведения). Если векторы и в правом ортонормированием базисе имеют координаты и соответственно, то векторное произведение этих векторов находится по формуле (1.15), которую принято записывать в виде
Если и — координатные столбцы векторов и в стандартном базисе, то координатный столбец векторного произведения находится по формуле
В самом деле, выполняя умножение матрицы на столбец, получаем
Пример 1.20. Параллелограмм построен на векторах (рис. 1.46). Найти:
Решение. а) Векторное произведение находим по формуле (1.16):
По указанной формуле получаем координатный столбец вектора :
Векторное произведение находим, используя алгебраические свойства:
б) Площадь параллелограмма находим как модуль векторного произведения :
Согласно его координатами служат направляющие косинусы
Вектор. Векторное произведение векторов.
Векторное произведение — это псевдовектор, который перпендикулярен плоскости, построенной по двум
сомножителям, которые являются результатом бинарной операции «векторное умножение» над
векторами в трёхмерном евклидовом пространстве.
Векторное произведение не имеет свойств коммутативности и ассоциативности (антикоммутативное)
Векторное произведение помогает в «измерении» перпендикулярности векторов — модуль
векторного произведения двух векторов равен произведению модулей этих векторов, если они
перпендикулярны, и стремится к нулю, если векторы параллельны или антипараллельны.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в
трёхмерной прямоугольной системе координат, формула для векторного произведения зависит
от ориентации прямоугольной системы координат или, говоря другими словами, её «хиральности».
Векторное произведение двух векторов обозначается квадратными скобками:
Свойства векторного произведения векторов.
1. Геометрический смысл векторного произведения векторов.
Векторным произведением вектора 

вектор 
параллелограмма, который построен на векторах 

перпендикулярный к плоскости этих векторов и направлен
так, чтоб самое маленькое вращение от 

вектора 
с конца вектора 

Модуль векторного произведения двух векторов 

Площадь треугольника строящегося на векторах 

векторного произведения векторов 

2. Вектор 




3. Вектор 






Векторное произведение векторов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
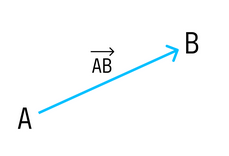
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
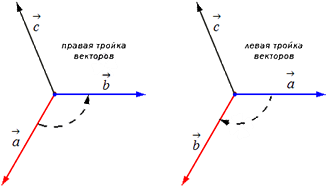
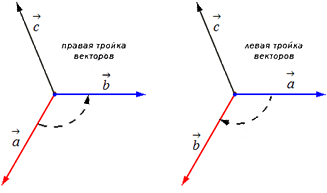
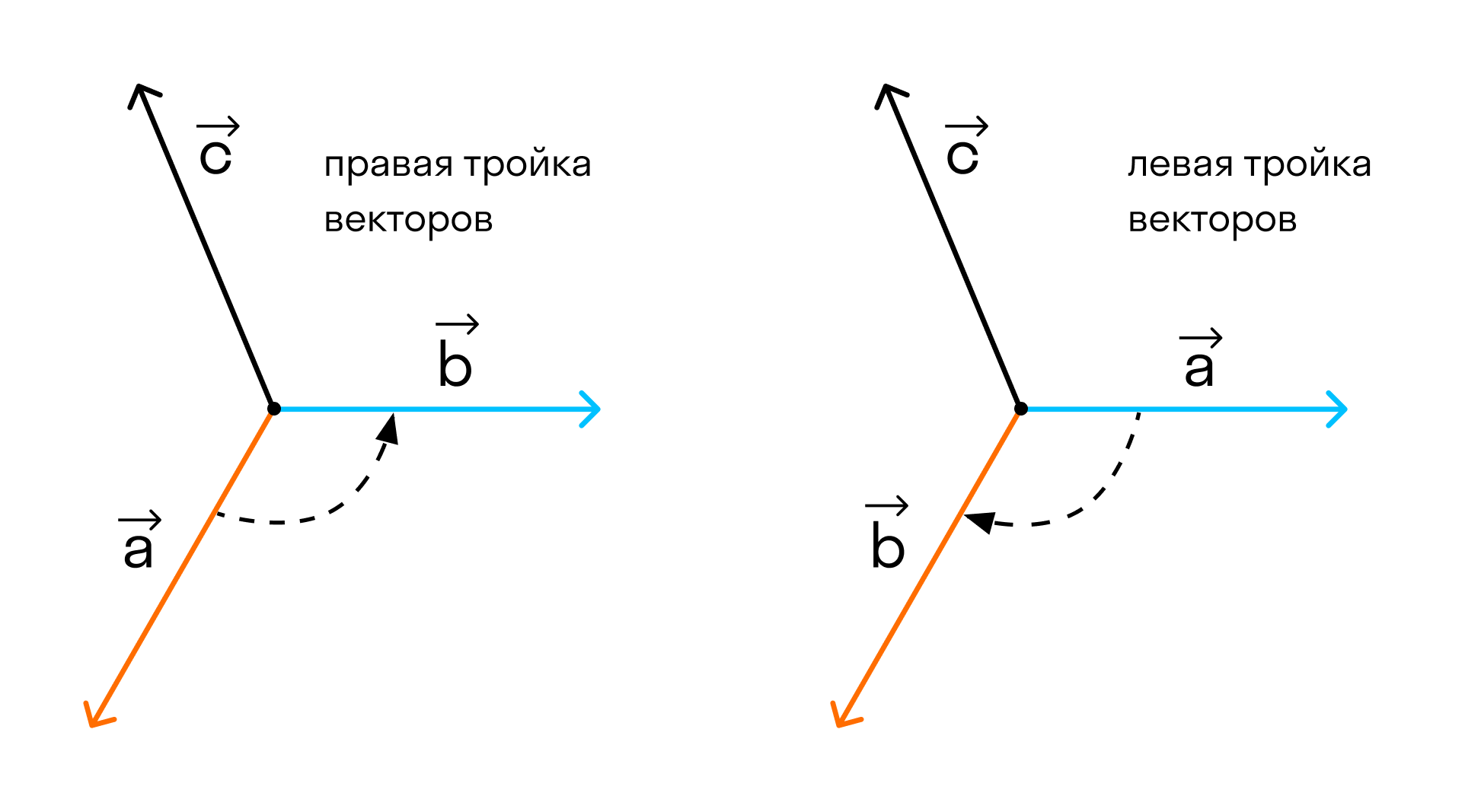
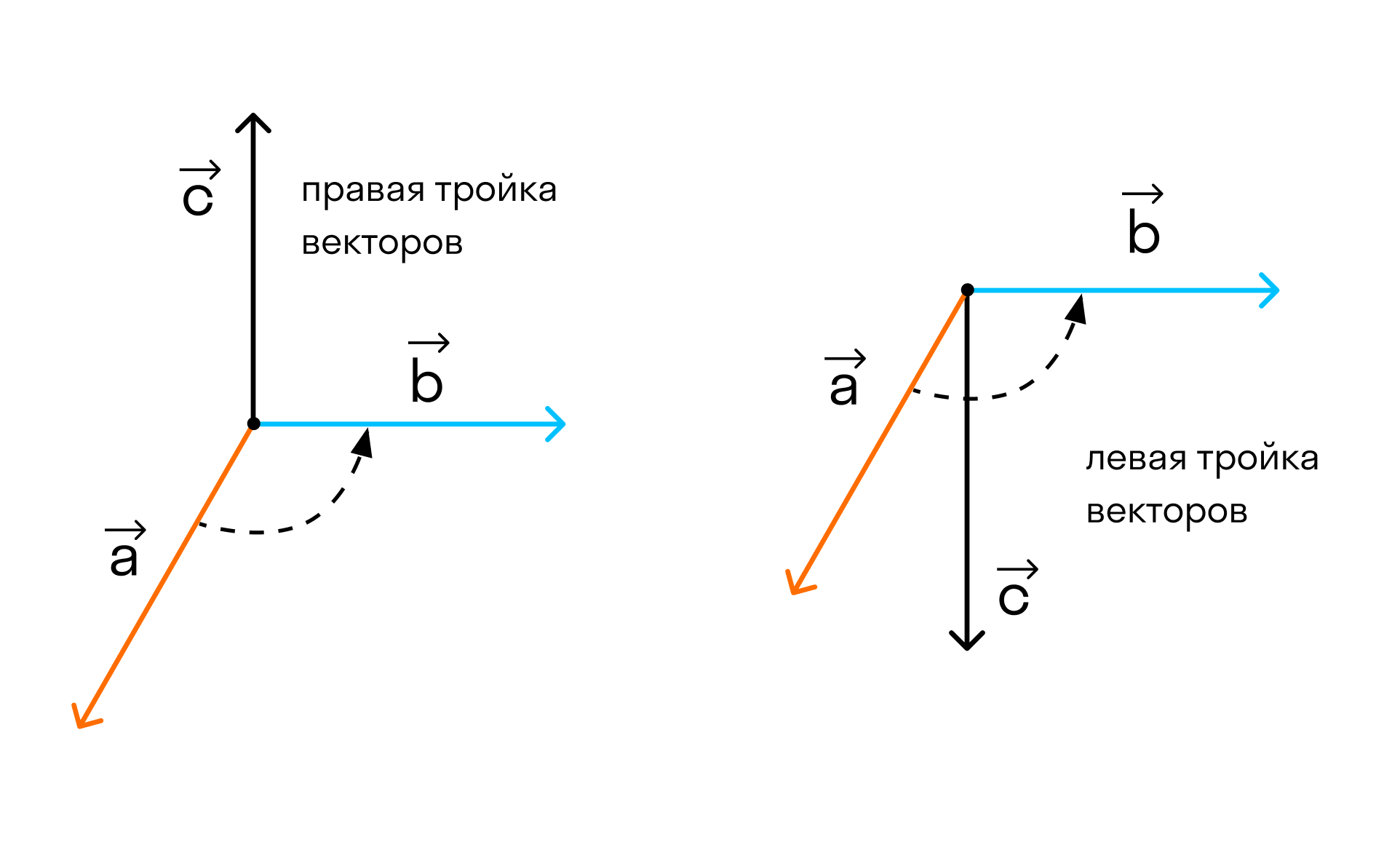
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
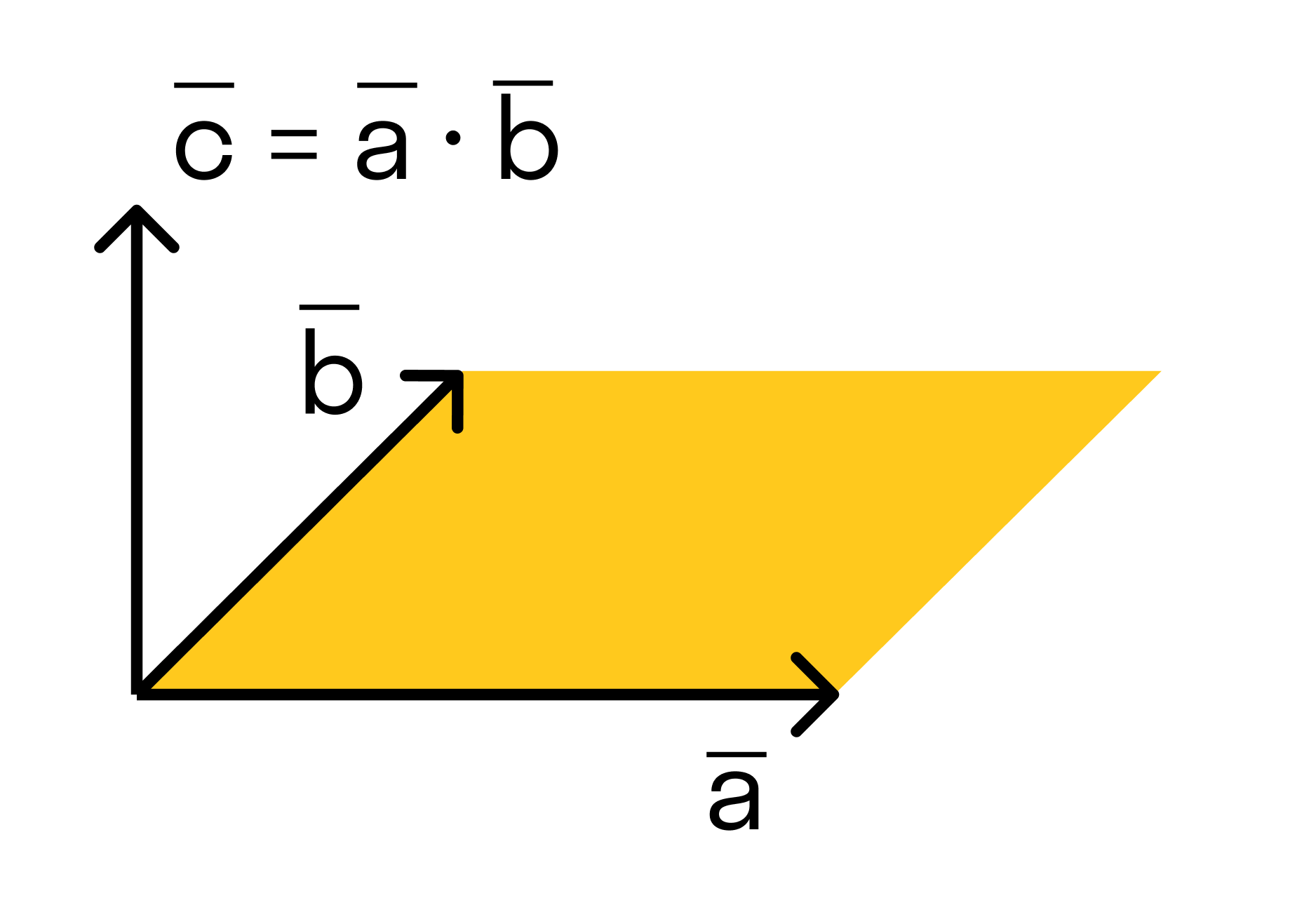
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a =
Векторное произведение векторов →a и →b обозначается как [→a • →b].
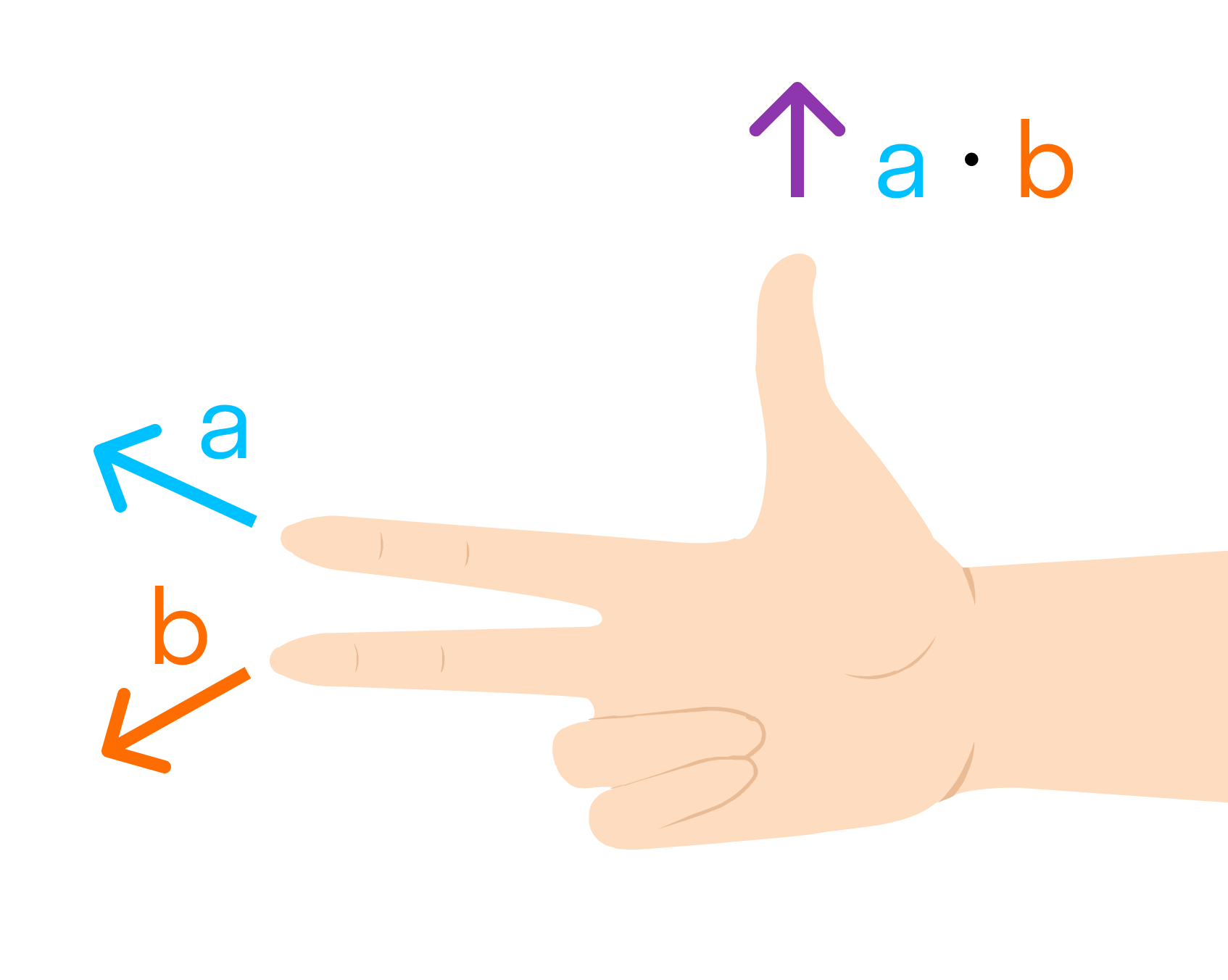
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.
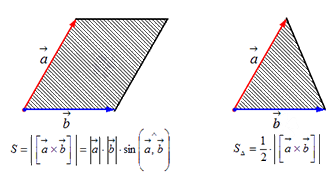
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
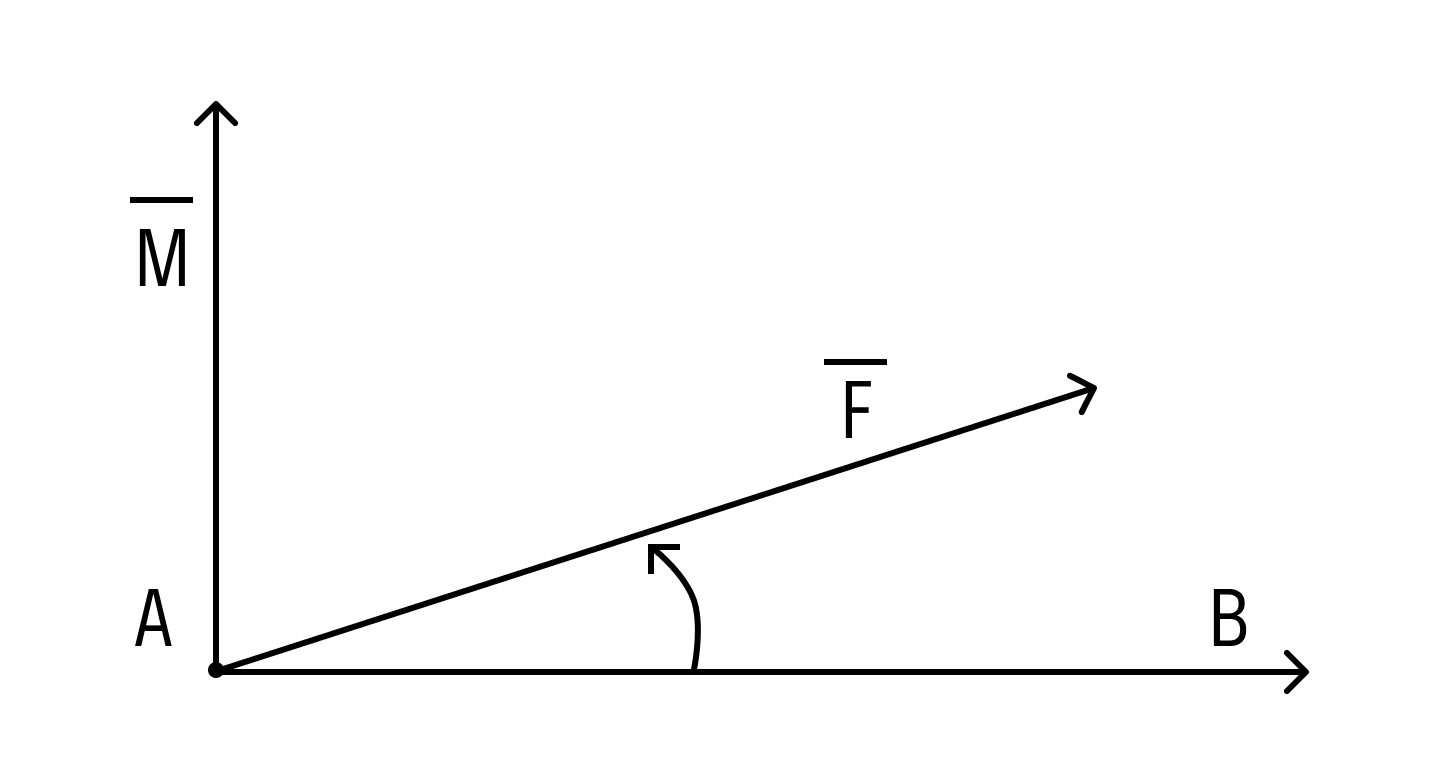
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Как вычислить векторное произведение векторов?
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.
Векторное Произведение Векторов. Свойства, определение
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a =
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
Координаты векторного произведения
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна. А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F]. Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!
Смешанное произведение векторов: свойства примеры и решения, геометрический смысл смешанного произведения векторов
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.
В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Умножение в системе координат
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Свойства операции умножения чаще всего требуются во время решения задач. Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.
Решение
По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)
Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→
Разбор типовых задач
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7
Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
Геометрический смысл
Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.
Данная формула и является геометрическим смыслом.