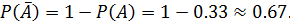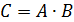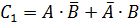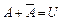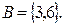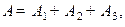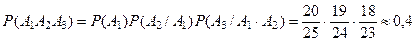Что называется произведением событий

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник

Понятия суммы и произведения событий

Сумма всех вероятностей событий выборочного пространства равняется 1. Например, если экспериментом является подбрасывание монеты при Событии А = «орел» и Событии В = «решка», то А и В представляют собой все выборочное пространство. Значит, Р(А) +Р(В) = 0.5 + 0.5 = 1.

Пример. В ранее предложенном примере вычисления вероятности извлечения из кармана халата красной ручки (это событие А), в котором лежат две синих и одна красная ручка, Р(А) = 1/3 ≈ 0.33, вероятность противоположного события – извлечения синей ручки – составит

Прежде чем перейти к основным теоремам, введем еще два более сложных понятия — сумма и произведение событий. Эти понятия отличны от привычных понятий суммы и произведения в арифметике. Сложение и умножение в теории вероятностей — символические операции, подчиненные определенным правилам и облегчающие логическое построение научных выводов.

Суммой нескольких событий является событие, заключающееся в появлении хотя бы одного из них. То есть, суммой двух событий А и В называется событие С, состоящее в появлении или события А, или события В, или событий А и В вместе.

Например, если пассажир ждет на остановке трамваев какой-либо из двух маршрутов, то нужное ему событие заключается в появлении трамвая первого маршрута (событие А), или трамвая второго маршрута (событие В), или в совместном появлении трамваев первого и второго маршрутов (событие С). На языке теории вероятностей это значит, что нужное пассажиру событие D заключается в появлении или события А, или события В, или события С, что символически запишется в виде:

Произведением двух событийА и В является событие, заключающееся в совместном появлении событий А и В. Произведением нескольких событий называется совместное появление всех этих событий.

В приведенном примере с пассажиром событие С (совместное появление трамваев двух маршрутов) представляет собой произведение двух событий А и В, что символически записывается следующим образом:

Допустим, что два врача порознь осматривают пациента с целью выявления конкретного заболевания. В процессе осмотров возможно появление следующих событий:

— обнаружение заболеваний первым врачом (А);

— необнаружение заболевания первым врачом ( );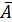

— обнаружение заболевания вторым врачом (В);

— необнаружение заболевания вторым врачом ( ).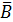

Рассмотрим событие, которое заключается в том, что заболевание будет обнаружено в процессе осмотров ровно один раз. Это событие может реализоваться двумя способами:

— заболевание обнаружит первый врач (А) и не обнаружит второй ( );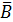

— заболеваний не обнаружит первый врач ( 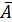) и обнаружит второй (B).

Обозначим рассматриваемое событие через 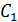и запишем символически:

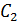
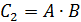
Рассмотрим событие, которое заключается в том, что заболевание будет обнаружено в процессе осмотров дважды (и первым, и вторым врачом). Обозначим это событие через и запишем: .

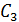
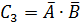
Событие, заключающееся в том, что ни первый, ни второй врач заболевания не обнаружит, обозначим через и запишем: .

Источник

Произведение событий. Теорема умножения вероятностей

Определение. Произведением или пересечением событий А и В называют событие, состоящее в одновременном наступлении событий и А, и В. Обозначение произведения: АВ или А 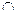В.

Пример. Двукратное попадание в цель есть произведение двух событий. Ответ на оба вопроса билета на экзамене есть произведение двух событий.

События А и В называют несовместными, если их произведение – событие невозможное, т.е. АВ = V.

События А – выпадение герба и В – выпадение цифры при однократном бросании монеты наступить одновременно не могут, их произведение событие невозможное, события А и В несовместные.

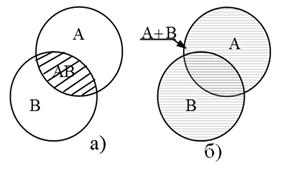
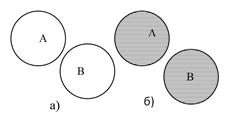
Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию.

Рис. 6.4. Геометрическая интерпретация произведения(а) и суммы(б) двух совместных событий

Пусть событие А – множество точек области А; событие В – множество точек области В. Заштрихованная область соответствует событию АВ на рис.6.4,а; событию 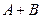на рис.6.4,б.

Для несовместных событий А и В имеем: АВ=V (рис.6.5,а). Событию А+В соответствует заштрихованная область на рис.6.5,б.

Рис. 6.5. Геометрическая интерпретация произведения(а) и суммы(б) двух несовместных событий

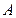
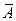
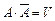
События и называют противоположными, если они несовместны и в сумме составляют достоверное событие, т.е.

;

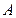
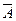
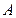
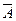
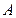
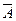
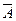
Например, произведем один выстрел по цели: событие – стрелок попал в цель, не попал; подброшена монета: событие – выпадение орла, − выпадение цифры; школьники пишут контрольную работу: событие – ни одной ошибки в контрольной работе, − есть ошибки в контрольной работе; студент пришел сдавать зачет: событие А − сдал зачет, − не сдал зачет.

В классе есть мальчики и девочки, отличники, хорошисты и троечники, изучающие английский и немецкий язык. Пусть событие M – мальчик, О – отличник, А – изучающий английский язык. Может ли случайно вышедший из класса ученик быть и мальчиком, и отличником, и изучающим английский язык? Это и будет произведение или пересечение событий МОА.

Пример. Бросают игральный кубик – куб, сделанный из однородного материала, грани которого занумерованы. Наблюдают за числом (числом очков), выпадающим на верхней грани. Пусть событие А – появление нечетного числа, событие В – появление числа, кратного трем. Найти исходы, составляющие каждое из событий: U, А, А+В, АВ и указать их смысл.

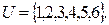
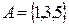
Решение. Исход – появление на верхней грани любого из чисел 1, 2, 3, 4, 5, 6. Множество всех исходов составляет пространство элементарных событий Ясно, что событие 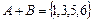, событие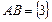

Событие − появление либо нечетного числа, либо числа, кратного трем. При перечислении исходов учтено, что каждый исход в множестве может содержаться только один раз.

Событие − появление и нечетного числа и числа, кратного трем.

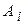
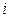
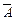
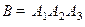
Пример. Проверено домашнее задание у трех студентов. Пусть событие − выполнение задания -м студентом, Каков смысл событий: и ?

Решение. Событие 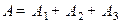− выполнение задания хотя бы одним студентом, т.е. или любым одним студентом (или первым, или вторым, или третьим), или любыми двумя, или всеми тремя.

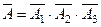
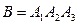
Событие − задание не выполнено ни одним студентом: ни первым, ни вторым, ни третьим. Событие − выполнение задания тремя студентами: и первым, и вторым, и третьим.

При рассмотрении совместного наступления нескольких событий возможны случаи, когда появление одного из них сказывается на возможности появления другого. Например, если осенью день солнечный, то менее вероятно, что погода испортится (начнется дождь). Если же солнца не видно, то больше шансов, что пойдет дождь.

Определение. Событие А называется независимым от события В, если вероятность события А не меняется в зависимости от того, произошло или нет событие В. Иначе событие А называется зависимым от события В. Два события А и В называются независимыми, если вероятность одного из них не зависит от появления или не появления другого, зависимыми – в противном случае. События называют попарно независимыми, если каждые два из них независимы друг от друга.

Теорема. (Умножения вероятностей) Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Р(А·В)=Р(А)·Р(В)

Эта теорема справедлива для любого конечного числа событий, если только они независимы в совокупности, т.е. вероятность любого из них не зависит от того, произошли или нет другие из этих событий.

Пример. Студент сдает три экзамена. Вероятность успешной сдачи первого экзамена 0,9, второго 0,65, третьего – 0,35. Найти вероятность того, что он не сдаст хотя бы один экзамен.

Решение: Обозначим А – событие студент не сдал хотя бы один экзамен. Тогда Р(А) = 1- Р(ùА), где ùА – противоположное событие студент сдал все экзамены. Поскольку сдача каждого экзамена не зависит от других экзаменов, то Р(А)=1-Р(ùА)= 1- 0,9*0,65*0,35=0,7953.

Определение. Вероятность события А, вычисленная при условии, что имеет место событие В, называется условной вероятностью события А при условии появления В и обозначается Р_В(А) или Р(А/В).

Теорема Вероятность появления произведения двух событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло:

Пример. Ученик дважды извлекает по одному билету из 34. Какова вероятность того, что он сдаст экзамен, если им подготовлено 30 билетов и в первый раз вынут неудачный билет?

Решение: Пусть событие А состоит в том, что в первый раз достался неудачный билет, событие В – во второй раз вынут удачный билет. Тогда А·В – ученик сдаст экзамен (при указанных обстоятельствах). События А и В зависимы, т.к. вероятность выбора удачного билета со второй попытки зависит от исхода первого выбора. Поэтому используем формулу (6):

Р(А·В) = Р(А)·РА(В) = (4/34)*(30/33)= 20/187

Заметим, что полученная в решении вероятность ≈0,107. Почему так мала вероятность сдачи экзамена, если выучено 30 билетов из 34 и дается две попытки?!

Теорема. (Расширенная теорема сложения) Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного появления (произведения):

Р(А+В)=Р(А)+Р(В)-Р(А·В).

Пример. Два студента решают задачу. Вероятность того, что первый студент решит задачу (событие А), равна 0,9; вероятность того, что второй студент решит задачу (событие В), равна 0,8. Какова вероятность того, что задача будет решена?

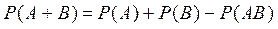
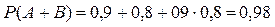
Решение. Нас интересует событие С, которое состоит в том, что задача будет решена, т.е. первым, или вторым студентом, или двумя студентами одновременно. Таким образом, интересующее нас событие С=А+В. События А и В совместны, значит применима теорема сложения вероятностей для случая совместных событий: . Для нашего случая (события А и В совместны, но независимы).

Пример Студент знает 20 вопросов из 25. Какова вероятность ответить на три вопроса, предложенных из 25?

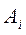
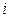
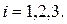
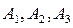
Решение. Введем событие − студент знает ответ на -й предложенный вопрос, События — зависимые. Поэтому

При отыскании вероятностей событий использовалось классическое определение вероятности.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Теория вероятности. Часть 2

В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.

Совместные и несовместные события

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.

События называются совместными, если наступление одного из них не исключает наступления другого.

Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.

Сумма событий

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.

При этом сумма двух несовместных событий есть сумма вероятностей этих событий:

Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:

Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.

Вероятность совместной реализации первых двух событий по условию равна 0,12.

Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть

Зависимые и независимые события

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.

Произведение вероятностей

Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:

Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: .

Подборку задач на отработку темы смотрите здесь.

Источник