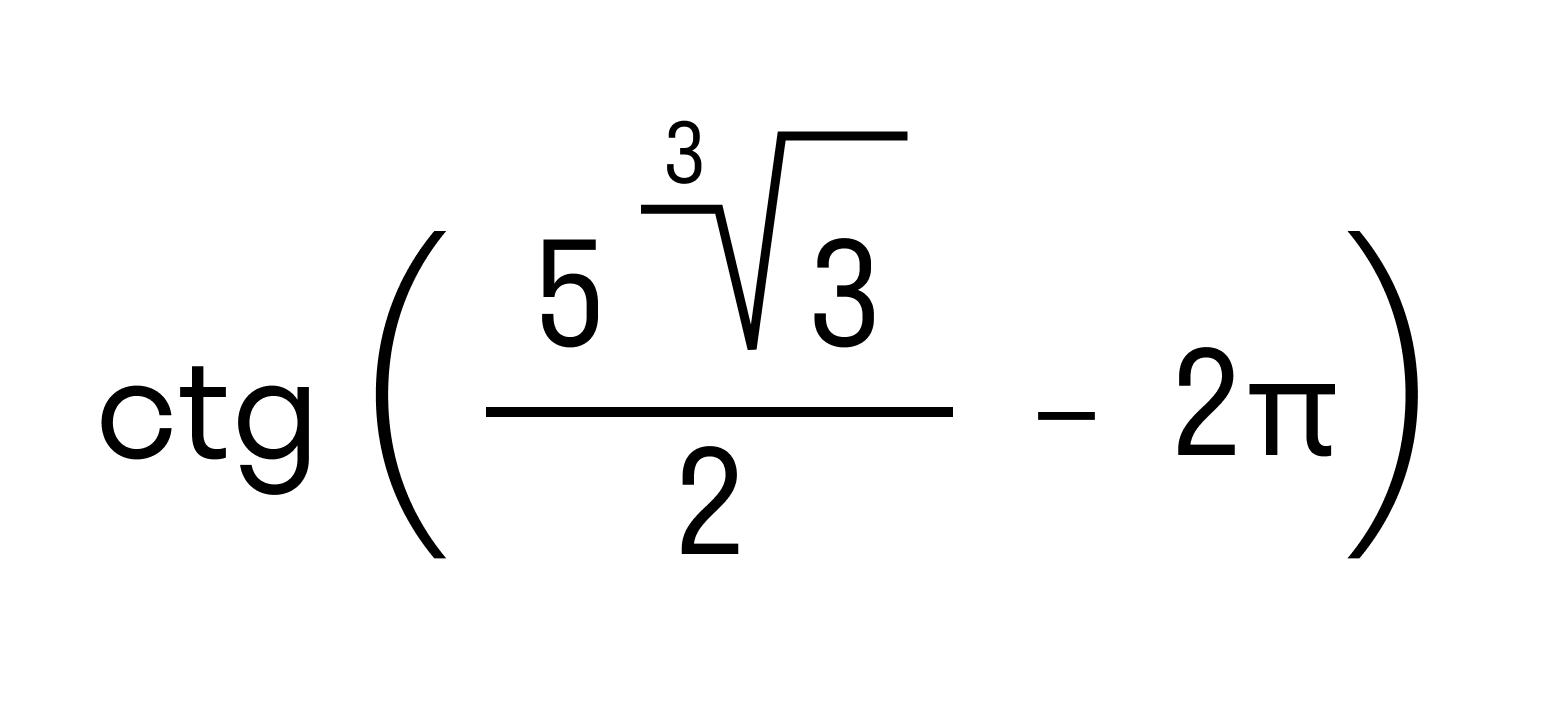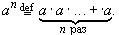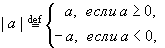Что называется произведением двух действительных чисел

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Арифметические операции над действительными числами

Вы будете перенаправлены на Автор24

Действительные числа

Множество действительных чисел состоит из множества рациональных и иррациональных чисел.

Обозначается множество действительных чисел R. Так же множество действительных чисел можно обозначить промежутком (-?; +?)

Вспомним, что любое рациональное число можно представить в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби, а любое иррациональное число можно представить в виде бесконечной десятичной непериодической дроби, значит будет верно следующее утверждение:

Множество конечных и бесконечных десятичных дробей составляют множество действительных чисел.

Геометрическая модель действительных чисел

Геометрической моделью действительных чисел является координатная прямая. Это связано с тем, что каждая точка числовой имеет координату, которая будет являться действительным числом.

Сравнение действительных чисел

Для того чтобы сравнить действительные числа, можно воспользоваться или геометрической моделью действительных чисел или провести сравнение аналитически.Рассмотрим данные способы.

Для того чтоюы сравнить два действительных числа, достаточно найти разность этих чисел и сравнить ее с нулем. Если разность будет положительна, то первое число(уменьшаемое разности) будет больше второго числа(вычитаемого разности); если же разность будет отрицательна, то наоборот

Решение. Для сравнения этих чисел составим и вычислим их разность

Теперь обратим вниманеи, что разность этих чисел получилась отрицательна, значит первое число( уменьшаемое) меньше второго(вычитаемого), т. е.

Готовые работы на аналогичную тему

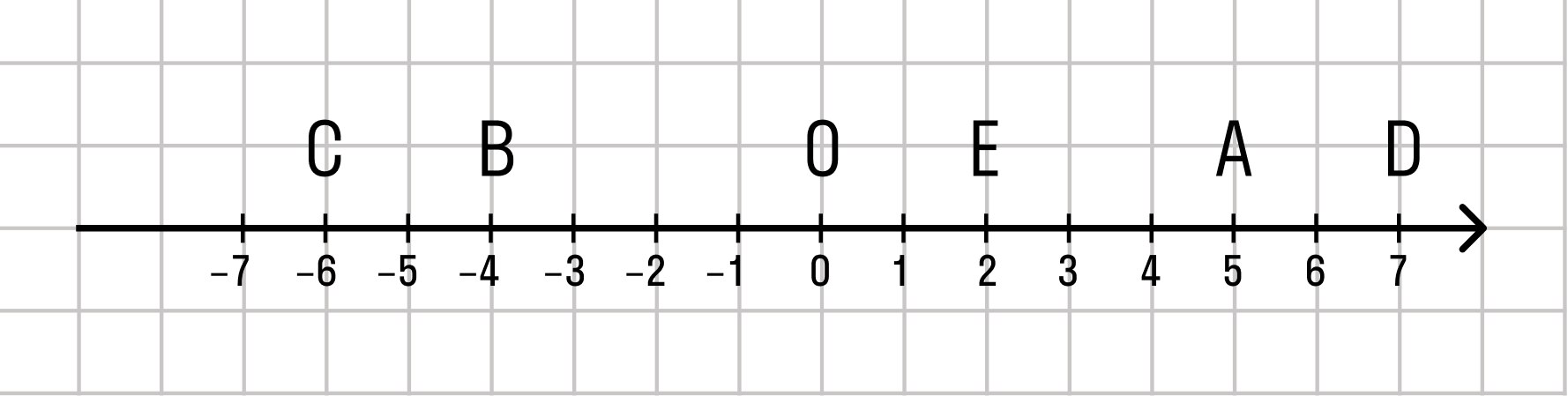
Для того чтобы сравнить числа с помощью числовой прямой, надо определить местоположение точек, координаты которых будут соответствовать сравниваемым действительным числам. То число, которое больше будет располагаться на координатной прямой правее, то, которое меньше левее

Мы видим, что вне зависимости от выбранного способа сравнения результат получен одинаковый.

С действительными числами можно осуществлять все арифметические операции: сложение, вычитание, умножение и деление. На практике часто, для того чтобы не допустить ошибку перед тем, как производить действия надо определить знаки исходных чисел, т.е. определить положительными или отрицательным является каждое из чисел

Сложение действительных чисел

Для того чтобы найти сумму действительных чисел с одинаковыми знаками, надо сложить модули этих чисел и перед полученной суммой поставить из общий знак.

Для того чтобы найти сумму чисел с разными знаками, надо из числа большего по модуля вычесть число меньшее по модулю и перед получившейся разностью поставить знак числа большего по модулю.

Теперь согласно правилу произведем дальнейший расчет

При вычисления произведения чисел необходимо придерживаться следующих правил:

при умножении и делении положительных чисел полученное число будет положительным

при умножении и делении отрицательных чисел полученное число будет положительным

при умножении и делении отрицательного и положительного чисел полученное число будет отрицательным

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 07 2021

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Арифметические операции над действительными числами

Геометрическая модель действительных чисел

Сравнение действительных чисел

Сравнение действительных чисел можно производить воспользовавшись либо геометрической моделью, либо их можно сравнивать аналитически. Рассмотрим оба способа сравнения. На координатной прямой расположено в произвольном порядке два числа. Определить, какое из них больше достаточно просто. Большее число всегда находится правее другого.

Аналитически определись какое число является большим или меньшим какого либо числа тоже возможно, для этого достаточно найти разность этих чисел и затем сравнить ее с нулем. Если полученная разность будет иметь положительный знак, то первое число (уменьшаемое разности) будет больше чем второе число (вычитаемое разности); если же разность будет иметь отрицательный знак, то первое число (уменьшаемое разности) будет меньше, чем второе число (вычитаемое разности).

Ниже рассмотрим примеры, демонстрирующие оба способа сравнения:

Для сравнения данных чисел найдем разность этих чисел.

Сравнить числа f r a c 185 и 4 с помощью координатной прямой.

Можно сделать вывод, что вне зависимости от внешнего вида сравнения действительных чисел можно реализовать все арифметические операции, а именно сложение, вычитание, умножение и деление. Однако перед выполнением действий с действительными числами следует учитывать исходные знаки данных чисел т.е. определить является каждое число положительными или отрицательными.

Сложение действительных чисел

Чтобы сложить два действительных числа с одинаковыми знаками следует сначала сложить их модули и затем перед суммой поставить их общий знак. Например:

Чтобы сложить два действительных числа с разными знаками следует для начала обратить внимание на знак числа, если знак одного из чисел отрицательный, тогда это число следует вычитать из другого, если положительный – сложить с другим. Далее нужно сложить либо вычесть данные числа и поставить знак большего модуля. Например

Вычитание действительных чисел

Умножение действительных чисел

Чтобы умножить (разделить) два действительных числа необходимо умножить (разделить) их модули. И затем перед результатом поставить знак по приведенному в таблице правилу знаков ниже.

При умножении и делении действительных чисел желательно помнить пословицу: «Друг моего друга — мой друг, враг моего врага — мой друг, друг моего врага — мой враг, враг моего друга — мой враг».

Свойства арифметических действий над действительными числами (основные законы алгебры)

В алгебре существуют так называемые основные законы алгебры. Они практически всегда принимаются за истину (случаи ложности данных законов не рассматриваем) и сформулированы в виде следующих свойств-тождеств:

Свойства 1 и 5 выражают переместительный закон (коммутативность) сложения и умножения соответственно;

Cвойства 2 и 6 выражают сочетательный закон (ассоциативность);

Cвойство 7 — распределительный закон (дистрибутивность) умножения относительно сложения;

Cвойства 3 и 8 указывают на наличие нейтрального элемента для сложения и умножения соответственно;

Cвойства 4 и 10 – на наличие нейтрализующего элемента соответственно.

Источник

Что называется произведением двух действительных чисел

йЪ ЬМЕНЕОФБТОПК НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП ДЕКУФЧЙФЕМШОЩЕ ЮЙУМБ НПЦОП УЛМБДЩЧБФШ, ЧЩЮЙФБФШ,
ХНОПЦБФШ, ДЕМЙФШ Й УТБЧОЙЧБФШ РП ЧЕМЙЮЙОЕ. рЕТЕЮЙУМЙН ПУОПЧОЩЕ УЧПКУФЧБ, ЛПФПТЩНЙ ПВМБДБАФ ЬФЙ ПРЕТБГЙЙ. нОПЦЕУФЧП ЧУЕИ ДЕКУФЧЙФЕМШОЩИ ЮЙУЕМ ВХДЕН ПВПЪОБЮБФШ ЮЕТЕЪ R , Б ЕЗП РПДНОПЦЕУФЧБ ОБЪЩЧБФШ ЮЙУМПЧЩНЙ НОПЦЕУФЧБНЙ.

II. пРЕТБГЙС ХНОПЦЕОЙС. дМС МАВПК РБТЩ ДЕКУФЧЙФЕМШОЩИ ЮЙУЕМ a Й b ПРТЕДЕМЕОП ЕДЙОУФЧЕООПЕ ЮЙУМП, ОБЪЩЧБЕНПЕ ЙИ РТПЙЪЧЕДЕОЙЕН Й ПВПЪОБЮБЕНПЕ ab, ФБЛПЕ, ЮФП ЧЩРПМОСАФУС УМЕДХАЭЙЕ ХУМПЧЙС:
II₁. ab = ba, a, b R .
II_2. a(bc) = (ab)c, a, b, c R.
II₃.уХЭЕУФЧХЕФ ФБЛПЕ ЮЙУМП, ОБЪЩЧБЕНПЕ ЕДЙОЙГЕК Й ПВПЪОБЮБЕНПЕ 1, ЮФП ДМС МАВПЗП a R ЧЩРПМОСЕФУС ХУМПЧЙЕ a1 = a.
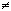
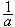
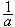
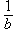
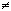
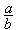
II₄. дМС МАВПЗП ЮЙУМБ a УХЭЕУФЧХЕФ ЮЙУМП, ОБЪЩЧБЕНПЕ ЕНХ ПВТБФОЩН Й ПВПЪОБЮБЕНПЕ ЙМЙ 1/a, ДМС ЛПФПТПЗП a=1. юЙУМП a, b 0, ОБЪЩЧБЕФУС ЮБУФОЩН ПФ ДЕМЕОЙС a ОБ b Й ПВПЪОБЮБЕФУС a:b ЙМЙ ЙМЙ a/b.

III. уЧСЪШ ПРЕТБГЙК УМПЦЕОЙС Й ХНОПЦЕОЙС:
ДМС МАВЩИ a, b, c R ЧЩРПМОСЕФУС ХУМПЧЙЕ (ac + b)c = ac + bc.

дЕКУФЧЙФЕМШОЩЕ ЮЙУМБ, ОЕ СЧМСАЭЙЕУС ТБГЙПОБМШОЩНЙ, ОБЪЩЧБАФУС ЙТТБГЙПОБМШОЩНЙ, ЙИ НОПЦЕУФЧП ПВПЪОБЮБЕФУС I. лТПНЕ ЮЕФЩТЕИ БТЙЖНЕФЙЮЕУЛЙИ ДЕКУФЧЙК ОБД ЮЙУМБНЙ НПЦОП
РТПЙЪЧПДЙФШ ДЕКУФЧЙС ЧПЪЧЕДЕОЙС Ч УФЕРЕОШ Й ЙЪЧМЕЮЕОЙС ЛПТОС.
дМС МАВПЗП ЮЙУМБ a R Й ОБФХТБМШОПЗП n УФЕРЕОШ a n ПРТЕДЕМСЕФУС ЛБЛ РТПЙЪЧЕДЕОЙЕ n УПНОПЦЙФЕМЕК, ТБЧОЩИ a:

фБЛЙН ПВТБЪПН, УФЕРЕОШ a r ПРТЕДЕМЕОБ ДМС МАВПЗП ТБГЙПОБМШОПЗП ЮЙУМБ r. йЪ ЕЕ ПРТЕДЕМЕОЙС УМЕДХЕФ, ЮФП ДМС МАВПЗП ТБГЙПОБМШОПЗП r ЙНЕЕФ НЕУФП ТБЧЕОУФЧП

уФЕРЕОШ a x (ЮЙУМП x ОБЪЩЧБЕФУС РПЛБЪБФЕМЕН УФЕРЕОЙ) ДМС МАВПЗП ДЕКУФЧЙФЕМШОПЗП ЮЙУМБ x РПМХЮБЕФУС У РПНПЭША ОЕРТЕТЩЧОПЗП ТБУРТПУФТБОЕОЙС УФЕРЕОЙ У ТБГЙПОБМШОЩН РПЛБЪБФЕМЕН (УН. ПВ ЬФПН Ч Р. 8.2). дМС МАВПЗП ЮЙУМБ a R ОЕПФТЙГБФЕМШОПЕ ЮЙУМП

ОБЪЩЧБЕФУС ЕЗП БВУПМАФОПК ЧЕМЙЮЙОПК ЙМЙ НПДХМЕН. дМС БВУПМАФОЩИ ЧЕМЙЮЙО ЮЙУЕМ УРТБЧЕДМЙЧЩ ОЕТБЧЕОУФЧБ

пОЙ ДПЛБЪЩЧБАФУС У РПНПЭША УЧПКУФЧ I-IV ДЕКУФЧЙФЕМШОЩИ ЮЙУЕМ.

Источник