Что называется прочностью жесткостью
Вопрос 1: Что называют прочностью, жесткостью, устойчивостью детали?
Лекция 1
Вопрос 1: Что называют прочностью, жесткостью, устойчивостью детали?
Вопрос 2: Чем отличаются нормальные напряжения от касательных?
Проекция вектора полного напряжения p на нормаль к данной площадке обозначается через σ и называется нормальным напряжением.
Составляющую, лежащую в сечении в данной площадке обозначается через τ и называется касательным напряжением.
Вопрос 3: Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними?
Ответ: Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними.
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой.
Вопрос 4: Какие нагрузки принято считать сосредоточенными?
Ответ: Воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий
Вопрос 5: Типы деформаций
Ответ: Растяжение, сжатие, сдвиг, изгиб, кручение.
Вопрос 6: Что такое сосредоточенная сила, распределенная нагрузка и момент?
К сосредоточенным относятся нагрузки, реальная площадь приложения которых несоизмеримо меньше полной площади поверхности тела.
Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная.
Вопрос 7: Сформулируйте закон Гука и принцип суперпозиции
Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняются принципу суперпозиции, или принципу независимости действия сил. В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил.
Вопрос 8: Что такое коэффициент Пуассона?
Величина отношения относительного поперечного сжатия к относительному продольному растяжению. Коэффициент зависит от природы материала, из которого изготовлен образец.
Вопрос 9: Что называется абсолютным удлинением?
Абсолютное удлинение показывает на сколько изменилась длина тела.
Вопрос 10: Что представляет собой допускаемое напряжение? Как его определяют?
Если установлен допускаемый коэффициент запаса прочности и для выбранного материала известно предельное напряжение, определяют максимальное напряжение, которое можно допустить для надежной работы элемента конструкции. Такое напряжение называют допускаемым
Лекция 2
Вопрос 1: В каких единицах измеряется напряжение?
Вопрос 2:. Что называется стержнем?
Лекция 3
Лекция 4
Лекция 5
Вопрос 6: Что такое срез?
Ответ: Развитие деформации сдвига приводит к разрушению, называемому срезом
Вопрос 7: Что такое смятие?
Ответ: Пластическая деформация, возникающую на поверхности контакта.
Лекция 6
Лекция 7
Лекция 8
Лекция 9
Лекция 10
Лекция 11
Лекция 1
Вопрос 1: Что называют прочностью, жесткостью, устойчивостью детали?
Разница между прочностью и жесткостью
Содержание:
Ключевые области покрыты
1. Что такое Сила
— определение, разные типы, деформация
2. Что такое жесткость
— определение, разные типы, формула
3. В чем разница между прочностью и жесткостью
— Сравнение основных различий
Ключевые слова: усталостная прочность, ударная вязкость, жесткость, прочность, предел прочности при растяжении, предел текучести
Что такое сила
Есть несколько разных терминов, используемых для описания силы. Все эти термины объясняют некоторые специфические физические свойства материи. Некоторые из этих терминов приведены ниже.
Рисунок 1: Типичная кривая напряжения-деформации для пластичного материала
Что такое жесткость
Жесткость может быть выражена следующим образом:
Рисунок 2: Жесткость вещества, которое можно согнуть
Разница между прочностью и жесткостью
Определение
способность
Прочность: Сила описывает способность объекта противостоять стрессу без разрушения или пластической деформации.
Жесткость: Жесткость описывает способность объекта противостоять деформации при приложении напряжения.
недостаточность
Прочность: Сила связана с физическим отказом вещества.
Жесткость: Жесткость связана с функциональной недостаточностью вещества.
Вещества
Прочность: Сила связана как с упругими, так и с хрупкими веществами.
Жесткость: Жесткость в основном применима к эластичным веществам.
Различные типы
Прочность: Различные типы прочности включают ударную вязкость, прочность на разрыв, усталостную прочность, предел текучести и т. Д.
Жесткость: Различные типы жесткости включают в себя жесткость при вращении и осевую жесткость.
Заключение
Ссылка:
1. «Прочность материалов». Википедия, Фонд Викимедиа, 13 января 2018 г.
Научная электронная библиотека
Лекция 1. ВВЕДЕНИЕ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Прочность, жесткость, устойчивость, – как понятия определяющие надёжность конструкций в их сопротивлении внешним воздействиям. Расчётные схемы (модели): твёрдого деформируемого тела, геометрических форм элементов конструкций. Внутренние силы в деформируемых телах и их количественные меры. Метод сечений. Напряжённое состояние. Перемещения и деформации. Понятия упругости и пластичности. Линейная упругость (закон Гука). Принцип независимости действия сил (принцип суперпозиции).
Основные понятия. Сопротивление материалов, наука о прочности (способности сопротивляться разрушению при действии сил) и деформируемости (изменении формы и размеров) элементов конструкций сооружений и деталей машин. Таким образом, данный раздел механики дает теоретические основы расчета прочности, жесткости и устойчивости инженерных конструкций.
Под нарушением прочности понимается не только разрушение конструкции, но и возникновение в ней больших пластических деформаций. Пластическая деформация – это часть деформации, которая не исчезает при разгрузке, а пластичность – способность материала сохранять деформацию.Возникновение пластических деформаций связано с нарушением нормальной работы конструкции и поэтому пластические деформации считаются недопустимым.
Жесткость – это способность конструкции (или материала) сопротивляться деформированию. Иногда деформация конструкции, отвечающей условию прочности, может воспрепятствовать нормальной ее эксплуатации. В таком случае конструкция имеет недостаточную жесткость.
Устойчивость – это способность конструкции сохранять положение равновесия, отвечающее действующей на нее нагрузке.
Конструкции, как правило, имеют сложную форму, отдельные элементы которой можно свести к простейшим типам, являющимисяосновными объектами изучения сопротивления материалов: стержни, пластинки, оболочки, массивы, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и динамических нагрузок, т.е. расчет реальной конструкции начинается с выбора расчетной схемы. Выбор расчетной схемы начинается со схематизации свойств материала и характера деформирования твердого тела, затем выполняется схематизация геометрической.Стержень – тело, у которого один размер (длина) значительно превышает два других размера.
Оболочка – это тело, ограниченное двумя криволинейными поверхностями, у которого один размер (толщина) много меньше двух других размеров. Пластина – это тело, ограниченное двумя параллельными плоскостями.
Массив – тело, у которого все три размера имеют один порядок.
Базируясь на законах и выводах теоретической механики, сопротивление материалов, помимо этого, учитывает способность реальных материалов деформироваться под действием внешних сил.
При выполнении расчетов принимаются допущения, связанные со свойствами материалов и с деформацией тела.
1. Материал считается однородным (независимо от его микроструктуры физико-механические свойства считаются одинаковыми во всех точках).
2. Материал полностью заполняет весь объем тела, без каких-либо пустот (тело рассматривается как сплошная среда).
3. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево).
4. Материал является идеально упругим (после снятия нагрузки все деформации полностью исчезают, т.е. геометрические размеры тела полностью или частично восстанавливаются). Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью.
5. Деформации тела считаются малыми по сравнению с его размерами. Это допущение называется принципом начальных размеров. Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции.
6. Перемещения точек тела пропорциональны нагрузкам, вызывающим эти перемещения (до определенной величины деформации материалов подчиняются закону Гука). Для линейно деформируемых конструкций справедлив принцип независимости действия сил (или принцип суперпозиции): результат действия группы сил не зависит от последовательности нагружения ими конструкции и равен сумме результатов действия каждой из этих сил в отдельности.
7. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения. Основанием для такого утверждения служит принцип Сен-Венана.
8. Принимается гипотеза плоских сечений (гипотеза Бернулли): плоские поперечные сечения стержня до деформации остаются плоскими и после деформации.
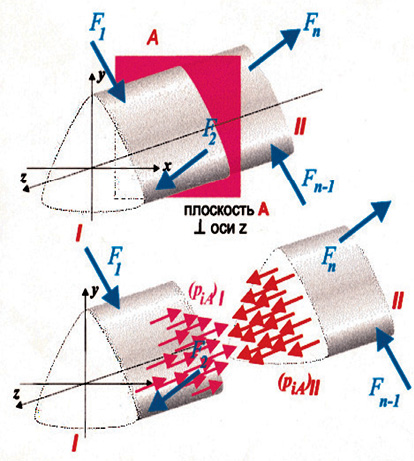
Внутри любого материала имеются внутренние межатомные силы. При деформации тела изменяются расстояния между его частицами, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. Для определения внутренних усилий используют метод сечения. Для этого тело мысленно рассекают плоскостью и рассматривают равновесие одной из его частей (рис. 4).
Рис. 4. Выявление внутренних усилий по методу сечений
Метод заключается в следующем:
1 Разрезаем систему (на части).
2. Отбрасываем одну часть.
3. Заменяем действие отброшенной части на оставшуюся внутренними силами упругости (приложим в сечении усилия, способные уравновесить внешние силы, действующие на отсеченную часть).
4. Составляем уравнения равновесия, составленное для отсеченной части и находим значения усилий.
Используем метод сечений и приведем внутренние силы к центру тяжести поперечного сечения стержня. В результате приведения мы получим результирующую силу R, равную главному вектору и пару сил с моментом M, равным главному моменту системы.
Проектируя R и M на координатные оси, получаем в общем случае 6 алгебраических величин – 6 внутренних силовых факторов:
Что называется прочностью, жесткостью?
Что называется прочностью, жесткостью?
Жесткостью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил, получая лишь малые упругие деформации.
Основные гипотезы сопротивления материалов.
При построении теории расчета невозможно отразить все многообразие свойств реальных материалов, поэтому приходится делать целый ряд допущений, упрощающих расчеты.
1. В курсе сопротивления материалов рассматривается идеализированное тело, которое считается сплошным (без пустот) и однородным.
Это означает, что свойства материала не зависят от формы и размера тела и одинаковы во всех его точках.
2. Упругие свойства материала во всех направлениях одинаковы, т.е. материал тела обладает упругой изотропией.
3. Тело считается абсолютно упругим, если после устранения причин, вызывающих деформацию, оно полностью восстанавливает свои первоначальные форму и размеры.
Это допущение справедливо лишь при напряжениях, не превышающих предел упругости.
4. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).
Закон Гука справедлив лишь при напряжениях, не превышающих предел пропорциональности.
5. Деформации элементов конструкции в большинстве случаев настолько малы, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояние от нагрузок до любых точек конструкции.
6. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности (принцип независимости действия сил).
Принцип независимости действия сил не распространяется на работу внешних и внутренних сил и на потенциальную энергию.
7. Поперечное сечение, плоское до деформации, остается плоским и после деформации (гипотеза плоских сечений Бернулли).
Понятие об изотропных и анизотропных материалах.
Упругость и пластичность
Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость — это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок. Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между.компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.
При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью. Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.
Понятие о моменте инерции.
Момент инерции, величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают Момент инерции осевые и центробежные. Осевым Момент инерции тела относительно оси z называется величина, определяемая равенством:
Центробежным Момент инерции относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:
или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси z от значений Ixz и Iyz зависят силы давления на подшипники, в которых закреплена ось.
Виды опор, расчетная схема.
17) Понятие о внутренних силовых факторах.
Внешние силы стремятся разрушить конструкции или узлы, а внутренние силы противодействуют этому.
| `P1 |
| `P2 |
| `P3 |
| `P4 |
| часть А |
| часть В |
Рассмотрим произвольный брус, нагруженный самоуравновешенной системой сил (рис. 1.1):
Рис. 1.1 Приведение внешних нагрузок
Чтобы найти внутренние силы воспользуемся методом сечений РОЗУ(рис. 1.2).
Р – разрезаем произвольной плоскостью на А и В.
О – отбрасываем одну из этих частей, например, В (рис. 1.2а). Рассмотрим оставшуюся часть(рис. 1.2б).
| `N |
| z |
| y |
| y |
| `Qx |
| `Qx |
| Mx |
| My |
| Mz |
З – заменяем. Внутренние силы мы заменяем главным вектором и главным моментом.
| `N |
| z |
| y |
| y |
| `Qx |
| `Qx |
а)
| `P2 |
| `P3 |
| часть А |
| `P |
| z |
| y |
| y |
| M |
Рис. 1.2 Метод сечений РОЗУ
Раскладываем главный вектор и главный момент в плоскости на оси (рис. 1.2в).
Внутренние силовые факторы:
Qx, Qy – вызывают сдвиг – перерезывающие поперечные силы;
N – нормальная продольная шина, растяжение, сжатие бруса;
Мz – крутящий момент;
Мx, Мy – изгибающий момент (рис. 1.2в).
В общем случае нагружения в сечении действуют 6 внутренних факторов. График изменения внутреннего фактора при передвижении вдоль оси стержня называется – эпюрой.
У – уравновешиваем.
Правило знаков для ВСФ.
Правило знаков для М
Эпюру для М строят на сжатых волокнах.
| Сжатые волокна |
| Сжатые волокна |
| — М |
| — М |
| + М |
| + М |
| + М |
| + М |
| — М |
| — М |
Рис. 3.3Связь между напряжениями и внутренними усилиями
Рис.2.1
Поместим начало плоской системы координат yz в центре тяжести левого сечения, а ось 
направим вдоль продольной оси стержня.
Для определения величин внутренних усилий воспользуемся методом сечений. Задавая некоторое сечение на расстояние z ( 
) от начала системы координат и рассматривая равновесие левой относительно заданного сечения части стержня (рис. 2.2, б), приходим к следующему уравнению:
,
откуда следует, что
.
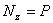
Следовательно, продольная сила в сечении численно равна сумме проекций на ось стержня всех сил, расположенных по одну сторону сечения
(2.1) 
Рис. 2.2
Для наглядного представления о характере распределения продольных сил по длине стержня строится эпюра продольных сил 
. Осью абсцисс служит ось стержня. Каждая ордината графика – продольная сила (в масштабе сил) в данном сечении стержня.
Эпюра позволяет определить, в каком сечении действует максимальное внутреннее усилие (например, найти Nmax при растяжении-сжатии). Сечение, где действует максимальное усилие будем называть опасным.
Отсутствует пример расчета. Его я не нашел к сожалению.
23) Определение деформации при растяжении-сжатии.
Абсолютная продольная и поперечная деформации равны
; 
.
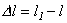
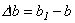
Относительная продольная деформация e и относительная поперечная деформация e‘ равны
; 
.
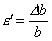
В пределах малых удлинений для большинства материалов справедлив закон Гука — нормальные напряжения в поперечном сечении прямо пропорциональны относительной линейной деформацииe
. (2.2)
Средние значения E и m для некоторых материалов даны в таблице 1.1.
Значения модуля упругости Е и коэффициента Пуассона n
| Материал | Е, МПа | n |
| Сталь | (2-2.2)×10 5 | 0.24-0.3 |
| Титан | 1.1×10 5 | 0.25 |
| Алюминий | 0.7×10 5 | 0.32-0.36 |
| Медь | 1.0×10 5 | 0.31-0.34 |
| Чугун | (1.1-1.6)×10 5 | 0.23-0.27 |
| Резина | 1.0-0.8 | 0.5 |
| Пробка | — | |
| Стекловолокно | (0.18-0.4)×10 5 | 0.25 |
| Дерево | 1×10 4 | — |
Так как , а 
, то подставляя в закон Гука (2.2) можно получить формулу для определения абсолютного удлинения (укорочения) стержня
.
Эта зависимость также выражает закон Гука.
Отношение относительной поперечной деформации e’ к относительной продольной деформации e, взятое по модулю, называется коэффициентом поперечной деформации или коэффициентом Пуассона
.
Эта величина является постоянной для каждого материала и определяется экспериментально.
Значения n для различных материалов изменяются в пределах 
(n = 0 у пробки, n = 0,5 у резины). Для большинства конструкционных материалов n =0,25…0,33 (табл. 1.1).
E и n являются основными характеристиками упругости изотропного материала.
24) Закон Гука при растяжении-сжатии и сдвиге.
Растяжение сжатие:
G — модуль сдвига или модуль упругости второго рода [МПа] — постоянная материала, характеризующая способность сопротивляться деформациям при сдвиге. (Е — модуль упругости, m— коэффициент Пуассона).
Вся потенциальная энергия при чистом сдвиге расходуется только на изменение формы, изменение объема при деформации сдвига равно нулю.
Закон Пуассона.
1) МО числа событий за время t: М = l*t.
2) среднеквадратическое отклонение числа событий 
, для данного распределения М = D.
Распределение Пуассона получается из биноминального, если число испытаний m неограниченно возрастает, а МО числа событий остается постоянным.
Закон Пуассона используется в том случае когда необходимо определить вероятность того что за данное время произойдет 1,2,3…отказов.
Вопрос найти не смог.
Рис.6.1
При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.
Если изгибающий момент 
является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.6.2). При наличии поперечной силы 
изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
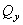
Косой изгиб — изгиб, при котором нагрузки действуют в одной плоскости, не совпадающей с главными плоскостями инерции.
Что называется прочностью, жесткостью?
Жесткостью называется способность элемента конструкции сопротивляться воздействию приложенных к нему сил, получая лишь малые упругие деформации.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
