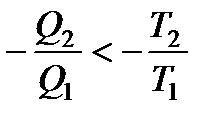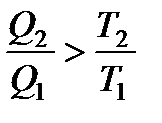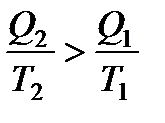Что называется приведенным количеством теплоты

Приведенное количество теплоты. Энтропия

Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно δQ/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:

(8.3)

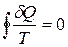
Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

(8.4)

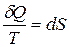
Функция состояния, дифференциалом которой является δQ/T, называется энтропией и обозначается S.

Из формулы (8.3) следует, что для обратимых процессов изменение энтропии

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

Выражения (8.5) и (8.6) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (8.5) и (8.6) можно представить в виде неравенства Клаузиуса

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (8.4), изменение энтропии

ΔS_1→2=S₂ – S₁= 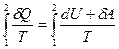. (8.8)

где подынтегральное выражение и пределы интегрирования определяются через величины, характеризующие исследуемый процесс. Формула (8.8) определяет энтропию, лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий.

Исходя из выражения (9.8), найдем изменение энтропии в процессах идеального газа. Так как dU=ν C_VdT, δΑ=pdV=ν RT 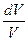, то

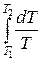
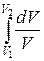
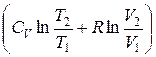
ΔS_1→2=S₂ – S₁= ν C_V + ν R = ν ,(8.9)

т. е. изменение энтропии ΔS_1→2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1→2.

Так как для адиабатического процесса δQ= 0, то ΔS=0 и, следовательно, S=const, т. е. адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы (8.9) следует, что при изотермическом процессе (T₁= Т₂)

ΔS= ν ,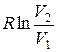

ΔS= ν .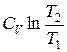

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свойством не обладают).

Более глубокий смысл энтропии вскрывается в статистической физике: энтропия связывается с термодинамической вероятностью состояния системы.

Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению, W> 1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя всегда

Отметим, однако, что эти утверждения, имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться, в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Приведенная теплота

Для обратимого цикла Карно коэффициент полезного действия можно вычислить по любой из полученных ранее формул

. (134)

(135)

. (136)

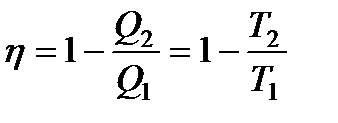
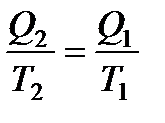
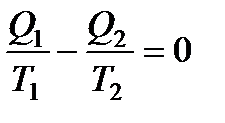
Поскольку Q₁ и Q₂ имеют разные знаки, то выражение (136) можно переписать в виде

, (137)

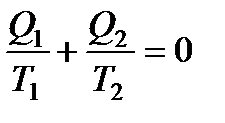
где величина Q считается положительной, если теплота передается рабочему телу, и отрицательной, если теплота отнимается.

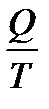
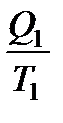
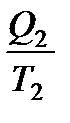
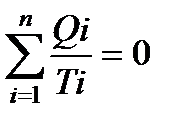
Отношение количества теплоты, подведенной к системе, к температуре, при которой это происходит, называется приведенной теплотой. Таким образом, –приведенная теплота, передаваемая системе. – приведенная теплота в 1-м изотермическом процессе, – приведенная теплота во 2-м изотермическом процессе. На адиабатических участках цикла Карно теплообмена с окружающей средой нет: Q=0. Следовательно, формула (137) учитывает всю теплоту, участвующую в цикле Карно. Таким образом, для обратимого цикла Карно

. (138)

Так как любой замкнутый цикл можно представить как сумму бесконечного числа циклов Карно, то для любого замкнутого обратимого цикла выражение (138) будет справедливо и его можно записать в следующем виде

. (139)

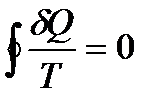
Последнее соотношение носит название равенства Клаузиуса.

КПД любого другого цикла меньше, чем КПД обратимого цикла Карно. Отсюда получаем:

.

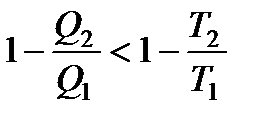
В итоге все вышеприведенные равенства превращаются в неравенства:

.

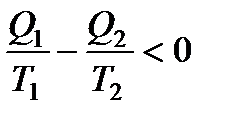
Учитывая, что теплота – величина алгебраическая, в итоге получаем:

,

(140)

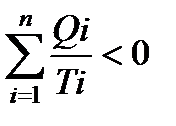
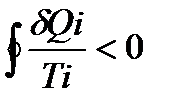
Уравнение (140) называется неравенством Клаузиуса.

Объединяя (139) и (140), можно записать

,

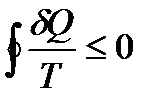
где знак равенства относится к обратимому процессу, а знак неравенства – к необратимому.

Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс) или меньше нуля (необратимый процесс).

Источник

Приведенное количество теплоты. Энтропия

Как уже говорилось выше, термический к.п.д. для обратимого цикла

(11.12)

Отсюда или (11.13)

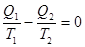
Учитывая, что теплота Q₂ отрицательна, выражение (11.13) примет вид

(11.14)

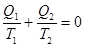
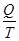
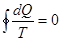
где называется приведенным количеством теплоты. Из выражения (11.14) следует, что для цикла Карно алгебраическая сумма приведенных количеств теплоты равная нулю. Для любого обратимого цикла

(11.15)

где 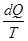– приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса.

Если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение является некоторой функцией состояния, не зависящей от пути.

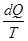
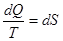
Функция состояния, дифференциалом которого является , называется энтропией S, т.е. (11.16)

Для обратимого процесса DS = 0, для необратимого DS > 0, т.е. в общем случае

Выражение (11.17) называется неравенством Клаузиуса и означает, что энтропия замкнутой системы либо возрастает, либо остается неизменной (энтропия не убывает). Реальные процессы необратимы, а следовательно, энтропия только возрастает. Это еще одна формулировка II начала термодинамики.

Опираясь на эту формулировку и на свой вывод о том, что все формы движения должны перейти в тепловую, Клаузиус пришел к выводу о неизбежности так называемой тепловой смерти Вселенной. Суть которой состоит в наступлении полного теплового равновесия в результате перехода тепла от более нагретого тела к менее нагретому.

Ошибочность такого вывода состоит в том, что II начало термодинамики применимо только к замкнутым системам. Такая безграничная и бесконечно развивающаяся система как вселенная не является замкнутой.

Физический смысл энтропия объяснил Больцман. Он же установил связь энтропии S с термодинамической вероятностью состояния системы

(11.17)

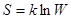
где k – постоянная Больцмана; W – термодинамическая вероятность, т.е. количество микросостояний, который определяют данное состояние.

Формула Больцмана (11.17) определяет статистический смысл энтропии, как меры неупорядоченности системы. В замкнутой системе процессы протекают в направлении увеличения количества возможных микросостояний. Иначе формулируя – система стремится от менее вероятного, к более вероятному неупорядоченному состоянию. Исходя из этого, можно дать еще одну формулировку II начала термодинамики: в замкнутой системе при обратимых провесах растет вероятность состояний, а при обратимых процессах, она остается неизменной.

Эта тема принадлежит разделу:

Механика

Механика.. молекулярная физика и.. механика..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Приведенное количество теплоты. Энтропия

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

И термодинамика
Курс лекций по физике для студентов инженерно-технических специальностей &n

Механика. Система отчета
Механика – раздел физики, изучающий закономерности механического движения и причины, вызывающие и изменяющие это движение. Механическое движение, заключается в изменении с течением

Перемещение и путь
Для изучения закономерностей физических процессов используют физические модели. Физической моделью, используемой для изучения законов механического движения является материальная точ

Скорость и ускорение
Рассмотрим движение материальной точки из положения А в положение В вдоль произвольной траектории

Движение материальной точки по окружности
Если материальная точка движется по окружности, то ее движение иногда удобнее oписывать не линейными величинами S,

Первый закон Ньютона. Инерциальная система отсчета
Как уже отмечалось выше, динамика, как раздел классической механики, изучает движение тел в зависимости от приложенных к ним сил. В основе динамики лежат три закона Ньютона. В качестве I з

Масса. Импульс. Закон сохранения импульса
Движущаяся материальная точка характеризуется импульсом (количеством движения). Вектор импульса материальной точки сонаправлен вектору скорости, а величина импульса пропорциональна величине скорост

Сила. Второй и третий законы Ньютона
При взаимодействии материальной точки с внешними телами ее импульс со временем изменяется. За меру изменения импульса принимается величина

Сила трения
При движении тела по горизонтальной поверхности на него действует сила, препятствующая движению – сила трения, то есть сила сопротивления, направленная в сторону противоположную перемещению.

Сила упругости
Как уже было отмечено выше, сила вызывает либо ускорение, либо деформацию тела. Деформация – это всякое изменение размеров или формы тела под действием внешних сил. Если после прекращения де

Сила тяготения
Ньютон, изучая движения планет на основании законов Кеплера[4] и законов динамики, установил закон всемирного тяготения. Этот закон сначала был сформулирован для планет, которые рассматривались как

Из формулы (2.27) видно, что
(2.29) Если тело находится на высоте h (r=R+h) то

Основное уравнение вращательного движения. Момент инерции
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси ОО (рис.3.3). Разобьём мысленно это тело на элементы массами Δm1, Δm2

Кинетическая энергия вращения
Рассмотрим вращение абсолютно твердого тела вокруг неподвижной оси ОО с угловой скоростью ω (рис. 3.7). Разобьем твердое тело на n элементарных масс ∆mi

Аналогия между поступательным и вращательным движением
Если сопоставить соотношения между величинами, характеризующими поступательное движение, с такими же соотношениями для вращательного движения вокруг оси, увидим аналогию между ними. Достаточно запо

Работа переменной силы. Мощность
Если под действием силы F происходит движение и тело перемещается на величину S, то говорят, что сила совершает работу. Работа – скалярная физическая величина, равная произведению про

Энергия. Кинетическая и потенциальная энергии
Тот факт, что тела могут совершать работу над другими телами, означает, что данные тела обладают энергией. Физическая величина, характеризующая способность тела или системы тел совершать работу наз

Закон сохранения энергии в механике
Полная механическая энергия Е тела равна сумме кинетической Ек и потенциальной Еn энергий: Е = Ек + Еn (4.20)

Основные характеристики колебательного движения
Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электр

Кинетическая, потенциальная и полная энергии гармонических колебаний
Полная энергия Е колеблющейся материальной точки равна сумме кинетической Ек и потенциальной Еп энергий Е = Ек + Еп

Физический маятник
Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О

Математический маятник
Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием си

Сложение гармонических колебаний одного направления
Если точка одновременно участвует в двух или нескольких колебаниях, то происходит сложение этих колебаний. Рассмотрим два случая: сложение гармонических колебаний, направленных по одной пр

Сложение взаимно перпендикулярных колебаний
Изучим результирующее колебание при сложении двух колебаний с одинаковыми циклическими частотами ω, происходящих во взаимно перпендикулярных направлениях вдоль осей Х и Y.

Возникновение волны. Продольные и поперечные волны
Если в среде колеблется частица, то она приводит в колебание соседние частицы. Процесс распространения колебаний называется волной. Направление распространения коле

Уравнение бегущей волны. Волновое уравнение
Уравнение бегущей волны выражает зависимость смещения колеблющейся частицы от координаты и времени. Рассмотрим вывод уравнения плоской синусоидальной волны. Пусть упругая волна распростран

Фазовая и групповая скорости
Скорость распространения фазы колебания называется фазовой скоростью. Если в линейной среде распространяются несколько волн, то к ним применим принцип суперпозиции (наложения) волн. Каждая в

Волны в упругих средах
Фазовая скорость распространения механических волн зависит от макроскопических свойств среды, таких, как плотность и упругость. Рассмотрим распространение механической

Звук и его характеристики
Распространяющиеся в среде упругие волны с частотами в пределах 16 – 20000 Гц называются звуковыми волнами. Волны указанного диапазона, воздействуя на слуховой аппарат, вызывают ощущение зву

Постулаты специальной теории относительности
Относительность времени Специальная теория относительности (СТО) представляет собой современную теорию пространства и времени. СТО иначе называется релятивис

Молекулярно-кинетический и термодинамический методы
При изучении строения веществ и их свойств используют два метода: – молекулярно-кинетический (молекулярно-статистический); – термодинамический. Молекулярно-кинети

Термодинамические параметры
При изучение свойств вещества термодинамическим методом используют понятие термодинамической системы, под которой понимается совокупность макроскопических тел (или составляющих тело

Основное уравнение молекулярно-кинетической теории газа
Основное уравнение молекулярно-кинетической теории устанавливает связь между давлением, объемом и кинетической энергией поступательного движения молекул.

Средняя кинетическая энергия молекул. Распределение молекул по степеням свободы
Выражение для энергии поступательного движения молекулы выведено для одноатомног

Скорости молекул. Распределение молекул по скоростям
Для характеристики скорости теплового движения выразим среднюю квадратичную скорость молекулы через температуру газа Т. Средняя кинетическая энергия ‹ε0›

Идеальный газ во внешнем поле
Если идеальный газ находится в силовом поле, то давление будет меняться от точки к точке, так как на молекулы газа действуют внешние силы. Рассмотрим наиболее простой случай, когда силы поля направ

Число соударений между молекулами и средняя длина свободного пробега молекул
В результате хаотического движения молекулы газа непрерывно сталкиваются друг с другом. Вычислим число соударений между молекулами для идеального газа. Для этого будем рассматривать молекулы, как у

Первое начало термодинамики
В термодинамике закон сохранения энергии выражается в виде I начала термодинамики, который формулируется следующим образом: теплота dQ, подведенная к замкнутой системе, расходуется на увелич

Теплоемкости газов
Удельной теплоемкостью вещества С называется количество теплоты dQ, необходимое для нагревания газа массой m = 1 кг на 1 градус

Работа газа при изопроцессах
В термодинамике изопроцессами называют процессы, при которых один из основных параметров сохраняется неизменным. В термодинамике работа расширения газа от объема V1 до

Адиабатический процесс
Адиабатическим называется такой процесс, когда между системой и окружающей средой отсутствует теплообмен (dQ = 0). Если dQ = 0, то из уравнения (10.22) следует, что

Круговые процессы (циклы)
Первое начало термодинамики, являющееся законом сохранения энергии, не указывает направления возможного протекания процессов. Любой процесс, при котором не нарушается закон сохранения энергии, возм

Второе начало термодинамики
Термодинамические процессы нельзя описать только первым началом термодинамики, который выражает закон сохранения и превращения энергии. Второе начало термодинамики определяет направление процесса и

Уравнение Ван-дер-Ваальса
Уравнение Менделеева-Клапейрона для одного моля идеального газа имеет вид

Изотермы Ван-дер-Ваальса и их анализ
После соответствующих преобразований уравнение (12.4) примет вид (12.6

Внутренняя энергия реального газа. Эффект Джоуля-Томсона
Как уже говорилось выше, для реального газа необходимо учитывать силы взаимодействия между молекулами. Силы притяжения между ними приводят к внутреннему давлению

Источник

Что называется приведенным количеством теплоты

Ранние работы по термодинамике были посвящены описанию количественных соотношений между теплотой и другими формами энергии. В настоящее время в этой области научных исследований наблюдается сдвиг от анализа энергетических изменений, сопровождающих превращения материи, в сторону использования термодинамики в качестве инструмента необходимого для понимания и предсказания поведения систем в связи с их энергетическими характеристиками.

Однако, термодинамика не отвечает на вопрос о том, какова величина теплового барьера, который должен быть преодолен для того, чтобы реакция пошла самопроизвольно. т.е. термодинамика изучает в основном конечные, равновесные состояния. Скорости и механизм реакции рассматривается в разделе, который носит название кинетики.

2.1. Первый закон термодинамики.

Начнем с определения.

Понятия энергии. Под понятием энергия обычно понимают “способность производить работу”. Решая какую-либо задачу методами термодинамики, необходимо прежде всего выделить из окружающего мира какую-то систему. Это может быть дождевая капля, двигатель, организм, планета и т.д. Если говорят, что выделенная система гомогенна, это означает, что свойства системы одинаковы во всех частях и система непрерывна от точки к точке. Если говорят, что система гетерогенна, это означает, что в ней присутствует не менее двух областей называемых фазами, которые отделены друг от друга поверхностями, называемыми границами раздела системы бывают двух типов: открытые и закрытые. В закрытой системе в ходе процесса происходит изменение энергии, но масса остается постоянной. В открытой системе может изменяться как энергия, так и масса.

Состояние системы определяется ее свойствами. Если изменяется одно из свойств, состояние системы меняется. При изучении системы обычно рассматриваются такие свойства, которые легко измерить. Это, в частности, температура, давление, объем, состав. Некоторые свойства взаимосвязаны, поэтому нет необходимости измерять их все одновременно.

К сожалению наши знания и возможности не позволяют вычислить (определить) весь запас энергии системы. Поэтому используется сравнительный подход. Часто энергия системы сравнивается с каким-либо стандартом (стандартным состоянием). Например газ обычно сравнивается с идеальным газом при стандартных условиях. Жидкий растворитель сравнивается с чистой жидкостью. Твердое вещество с его наиболее стабильной кристаллической формой. Такие состояния, называемые стандартными, представляют собой точки отсчета, относительно которых измеряют изменение в системе.

2.2 Формулировка первого закона

Есть несколько формулировок первого закона термодинамики. Если одна из них принимается в качестве основной, то все другие являются следствиями, вытекающими из нее.

Первая формулировка звучит следующим образом:

Энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах.

Следствием из этого закона является то, что невозможен вечный двигатель первого рода, т.е. нельзя создать такой двигатель, который совершил бы работу без затраты энергии. Создание такого двигателя возможно только в том случае, если неверен первый закон.

Внутренняя энергии изолированной системы есть величина постоянная.

Если данной системе передается некоторое количество энергии в форме тепла Q, которое идет только на приращение внутренней энергии системы D U и на совершение системой работы W, то согласно первому началу:

для бесконечно малых изменений:

Уравнения (1) и (2) являются математическим выражением первого начала термодинамики.

Справедливость этого утверждения можно доказать следующим образом.

Предположим, что в состоянии (I) внутренняя энергия системы U₁. Из этого состояния система переходит в состояние (2), в котором ее внутренняя энергия равна U₂.

В отличие от D U величины Q и W в общем случае зависят от пути процесса. Поэтому в уравнении (2) dU является полным дифференциалом, в то время как d Q и d W просто бесконечно малыми величинами

2.3. Применение первого начала термодинамики к различным процессам.

Если система совершает работа W только против внешнего давления, то

или для эмпирического процесса

Математическое выражение первого начала термодинамики в этом случае имеет вид:

или d Q = dU + pdV (6)

Для изохорного процесса (V = const) p D V = 0 и следовательно :

где Q_V теплота, сообщаемая системе в изохорном процессе. Из уравнения (7) и (8) следует, что в изохорном процессе тепла, сообщаемое системе, идет только на приращение внутренней энергии системы. В этом случае Q_V не зависит от пути перехода системы из одного состояния в другое и d Q_v является полным дифференциалом, т.е. функцией состояния.

Это означает, что изменение внутренней энергии системы D U в изохорном процессе определяется теплотой процесса Q_v и может быть измерено калориметрически.

В случае изобарного процесса (р= const).

Эту функцию состояния называют энтальпия и обозначают

Из уравнений (9 ) и ( 10) следует, что

Таким образом, в изобарном процессе все тепло сообщенное системе идет на приращение ее энтальпии. В этом случае Q_p также не зависит от луча перехода системы из одного состояния в другое и d Q_р является полным дифференциалом.

Из уравнения(11) и(12) следует также, что изменение энтальпии системы D Н в изобарном процессе определяется теплотой процесса Q_p и может быть измерено калориметрически.

В адиобатном процессе, т.е. в процессе, в котором система не обменивается с окружающей средой теплотой работа совершается за счет уменьшения внутренней энергии системы:

Изотермический процесс характеризуется T = const, для такого процесса dU = 0, тогда d Q = D W_T, т.е. вся сообщенная системе теплота превращается в работу, величина которой определяется уравнением:

Используя уравнение состояния газа Менделеева-Клапейрона, найдем, что для 1 моль идеального газа :

2.4. Теплота химической реакции.

Установим связи между Q_p и Q_v.

В соответствии с уравнение (10) имеем:

D Н = D U + p D V, но из уравнения (11) и (7) следует, что

Q_p = D Н, а D Н = D U, то Q_p = Q_v + p D V

Другими словами, D n изменение числа молей реагирующих веществ в результате протекания реакции.

Если реакция протекает в конденсированной системе, то объем системы меняется мало и в этом случае Q_p и Q_v приблизительно равны.

Изучая тепловые эффекты разных химических реакций, русский ученый Г.М. Гесс в 1840 году установил закон, который назван его именем.

Закон утверждает, что “теплота химической реакции, протекающей при постоянном объеме или постоянном давлении, определяется только природой исходных веществ и продуктов и не зависит от числа и последовательности промежуточных стадий при условии, что теплоты измерены при одинаковых температурах”.

Интересно, что закон Гесса был открыт раньше установления первого начала термодинамики. После установления первого начала стало ясно, что закон Гесса является одним из следствий этого начала, согласно которому Q_v = D U и Q_p = D H не зависят от пути процесса. Закон Гесса имеет большое практическое значение,т.к. позволяет рассчитать теплоты химических реакций, для которых они не могут быть определены экспериментально или это очень сложно сделать. Обычно для этого решают систему термохимических уравнений. Термохимическим называют такое уравнение, в котором в правой части наряду с химическими формулами продуктов реакции указывают теплоту реакции. При этом для реагирующих веществ указывается агрегатное состояние участников реакции. Если вещество в твердом состоянии существует в нескольких полиморфных модификациях, то необходимо указать эту модификацию.

Стехиометрические коэффициенты могут быть и дробными, т.к. они указывают молярные количества реагирующих веществ.

С термохимическими уравнениями можно проводить такие же математические операции, как и с алгебраическими уравнениями. Например, превращение глюкозы в молочную кислоты, при анаэробной ферментации используется некоторыми микроорганизмами для получения энергии.

Непосредственно измерить теплоту этого процесса трудно, поскольку параллельно с молочной кислотой образуются и другие продукты.

Однако можно экспериментально определить теплоты следующих реакции:

Вычитая из уравнения 1 удвоенное 2 и затем 3, получим:

2.6. Следствие из закона Гесса

Расчеты теплот химических реакций с использованием закона Гесса значительно упрощается, если воспользоваться так называемыми стандартными теплотами горения.

а) Расчет теплового эффекта химической реакции постандартным теплотам образования.

Стандартной теплотой образования вещества называют теплоту, которая выделяется или поглощается при образовании одного моля данного вещества в стандартном состоянии из простых веществ, взятых в стандартном состоянии при данной температуре.

Согласно проведенной формулировке теплотой образования СаСо₃ будет тепловой эффект следующей реакции:

Из закона Гесса следует, что теплота химической реакции равна алгебраической сумме теплот образования реагирующих веществ с учетом их стехиометрических коэффициентов, причем теплоты образования продуктов реакции берут со знаком плюс, а теплоты образования исходных веществ со знаком минус.

Рассмотрим в качестве примеров реакцию получения глюкозы из СО₂ и Н₂О

Суммарное уравнение реакции можно записать:

Приведение уравнения можно получить следующим образом.

Умножим уравнение 1 и 2 на 6, а затем их сумму вычтем из уравнения 3:

После алгебраических преобразований получим:

Воспользовавшись стандартными значениями теплот образования участников реакции, получим:

б) Расчеты теплот сгорания.

Стандартной теплотой сгорания называют теплоту, выделяющегося при окислении одного моля вещества, взятого в стандартном состоянии при данной температуре, кислородом до конечного продуктов окисления.

Из закона Гесса следует, что теплота химической реакции равна алгебраической сумме теплот сгорания реагирующих веществ с учетом их стехиометрических коэффициентов, причем, теплоты сгорания продуктов реакции берут со знаком минус, а теплоты сгорания исходных веществ со знаком плюс:

в) Теплота нейтрализации.

Теплотой нейтрализации называют теплоту, необходимую для нейтрализации одного мольэквивалента кислоты одним моль-эквивалентом основания.

Теплота нейтрализации сильных кислот сильными основаниями не зависит от природы кислоты и основания.

Тепловой эффект приведенных реакции практически одинаков и равен

В случае реакции нейтрализации слабых кислот и слабых оснований такого постоянства не наблюдается, так как часть тепла расходуется на ионизацию слабой кислоты или слабого основания.

г) Теплота растворения

В зависимости от природы растворенного вещества и природы растворителя процесс растворения сопровождается выделением или поглощением тепла.

Мольной теплотой растворения называют количество тепла, выделяющееся и поглощающееся при растворении одного моля вещества. в таком объеме растворителя, когда его дальнейшее прибавление не вызывает выделение или поглощение тепла.

Обычно при определении теплоты растворения берется более чем 300-кратный избыток растворителя.

Теплота растворения твердых тел представляет собой теплоту разрушения кристаллической решетки D Нр и теплоту сольватации D Нс

D Н_раств. = D Нр + D Нс

Для разрушения кристаллической решетки необходимо затратить некоторое к-во энергии, поэтому теплота этого процесса будет положительна.

Сольватация всегда сопровождается выделением тепла и, следовательно, теплота этого процесса отрицательна. Отсюда следует, что теплота растворения может быть как положительной, так и отрицательной.

Отрицательная теплота растворения указывает на то, что количество теплоты, выделяющееся при сольватации, больше, чем энергия, необходимая для разрушения кристаллической решетки. В случае положительной теплоты растворения количество энергии, необходимое для разрушения кристаллической решетки, больше энергии, которая выделяется при сольватации.

В тех случаях, когда в качестве растворителя используют воду, теплота, которая выделяется при взаимодействии растворенного вещества с растворителем, называется теплотой гидратации.

Теплоту гидратации, в соответствии с законом Гесса, расчитывают по разности между теплотой растворения безводного соединения и теплотой растворения гидрата.

Указанное уравнение можно получить комбинацией следующих

Вычтем из уравнения 1 уравнение 2:

После преобразования получим:

Источник