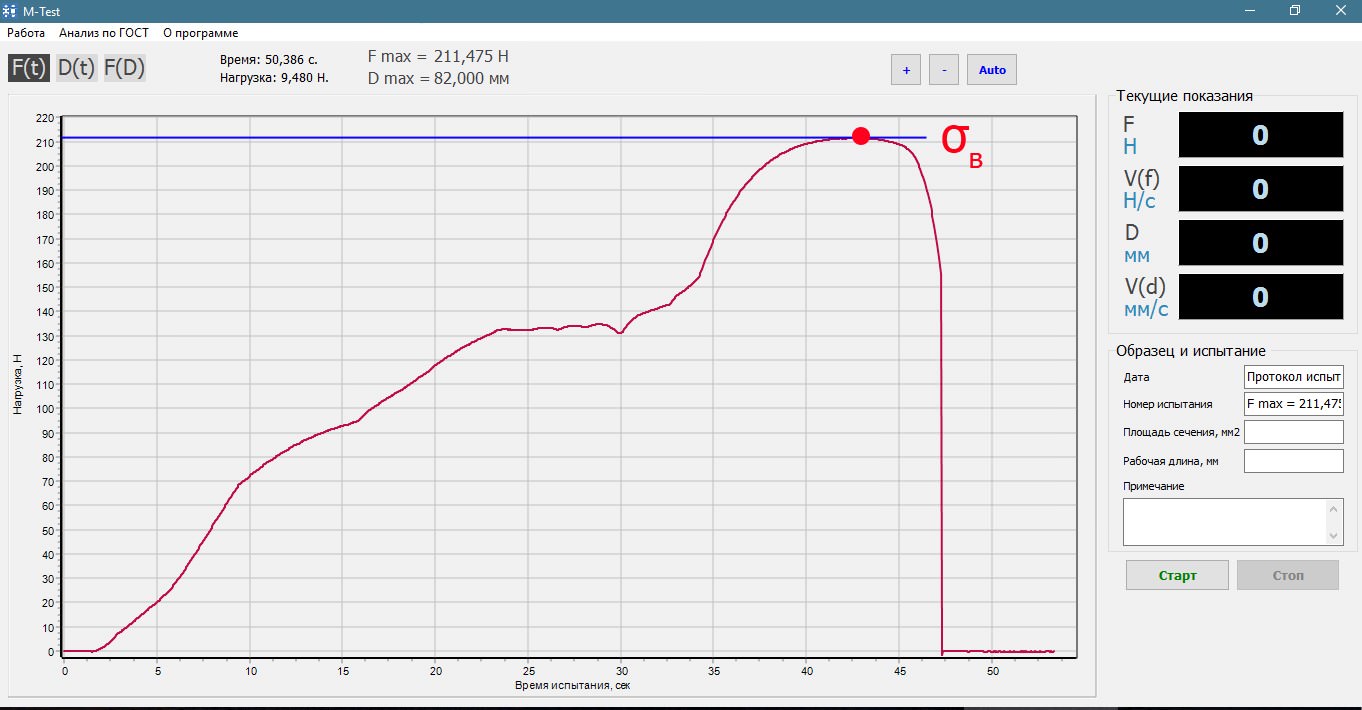
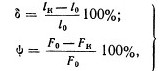Что называется пределом пропорциональности пределом текучести пределом прочности
Свойства, определяемые испытанием на растяжение, и факторы, на них влияющие
1. Предел прочности
Пределом прочности называют максимальное усилие растяжения, отнесенное к единице площади его первоначального сечения
Другими словами, предел прочности есть условное максимальное напряжение, которое выдерживает материал при растяжении. Под «истинным пределом прочности»(или под действительным сопротивлением разрыву) понимается усилие в момент разрыва P, отнесенное к площади сечения.
2. Предел пропорциональности и упругости
3. Предел текучести
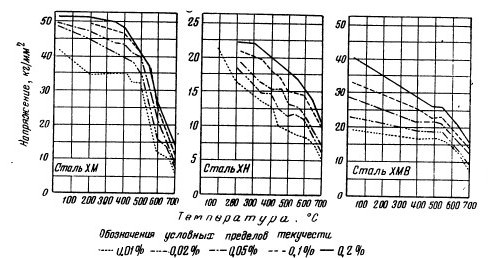
Пределом текучести σТ называется напряжение, при котором возникающая остаточная деформация образца распространяется равномерно по его рабочей части при временном постоянстве растягивающего усилия.
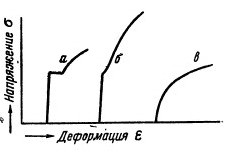
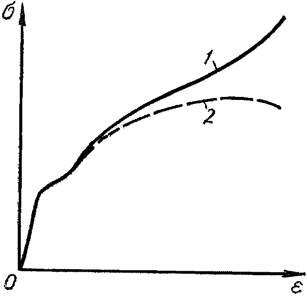
В некоторых случаях площадка текучести бывает неясно выражена (кривая б) или совершенно отсутствует (кривая в); такую форму кривых при нормальной температуре испытания имеют весьма пластичные металлы (например, медь). С повышением же температуре явным пределом текучести, форма кривой имеет вид, показанный на рисунке, в. Мягкая углеродистая сталь с содержанием 0,05% при 300°С дает кривую, соответствующую кривой б; другие, более теплоустойчивые стали сохраняют явный предел текучести до 400 и даже до 500°С; выше этих температур форма кривых растяжения аналогична кривой в.
Во всех случаях, когда отсутствует явный предел текучести, приходится прибегать к нахождению так называемых условных пределов текучести, основанных на определении напряжений, вызывающих заданную остаточную деформацию небольшой величины (в пределах 0,01—0,5%). Чаще всего на практике определяют условные пределы текучести, вызывающие остаточную деформацию, равную 0,1 или 0,2%.
Условные пределы текучести некоторых легированных сталей
Если условные пределы текучести при нормальной температуре мало различаются между собой, то при высоких температурах разница между условными пределами текучести, например 0,01 и 0,2% (после текучести), становится значительной.
4. Удлинение и поперечное сужение образца
Удлинение и поперечное сужение образца, испытанного при высокой температуре, являются показателями пластических свойств металла при данной температуре.
Удлинение δ и поперечное сужение ψ замеряются на охлажденных образцах и подсчитываются по общеизвестным формулам:
Наибольшее влияние на эти свойства оказывает время до разрыва или, что то же самое, скорость растяжения образца.
5. Модуль упругости
Модуль нормальной упругости E является важной физико-механической характеристикой металла. Знание величины модуля упругости стали для широкого диапазона температур необходимо не только при конструкторских расчетах деталей машин и аппаратуры, работающих при повышенных температурах, но и в ряде других случаев.
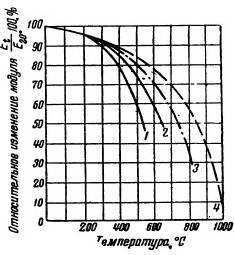
Относительное изменение модуля упругости E (в % от его значения при 20°) в зависимости от температуры для сталей: 1-нелегированной; 2-низколегированной; 3-среднелегированной; 4-высоколегированной
Лекция 2. Упругие и прочностные характеристики материалов
Значение некоторых употребляемых в данной статье понятий и определений приводится отдельно.
Геометрические характеристики рассматриваемого тела, уравнения равновесия и метод сечений позволяют определить значение напряжений в любой точке рассматриваемого сечения. Соответственно суть расчета на прочность сводится к тому, что напряжение σ в наиболее нагруженной точке (на некоторой элементарной площади) должно быть меньше или равно сопротивлению материала:
σ ≤ R (318.1)
Диаграммы напряжений
На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.
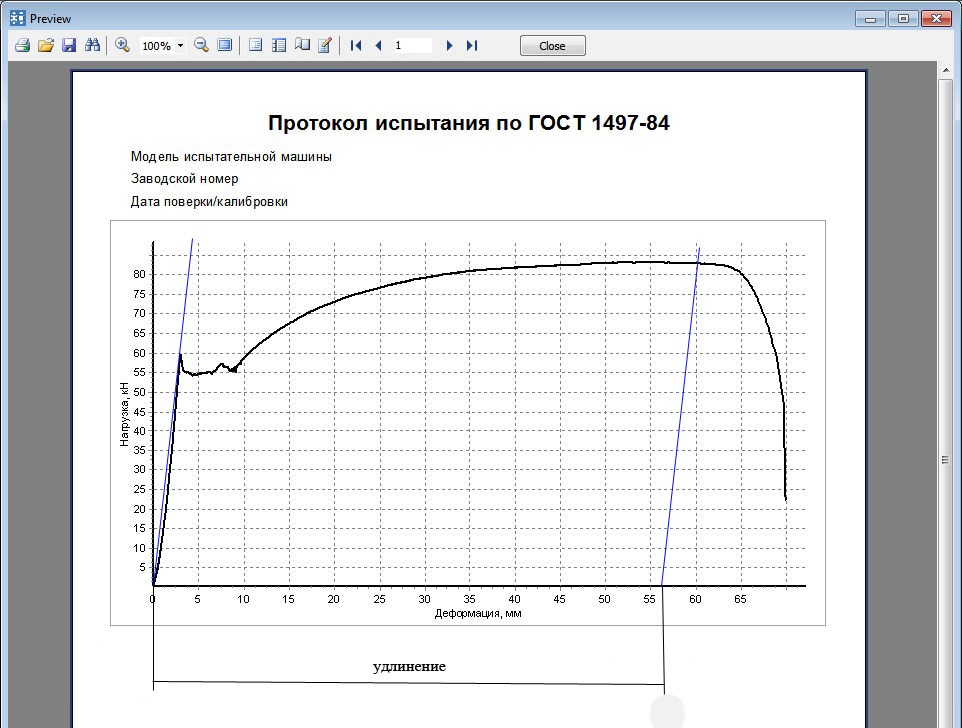
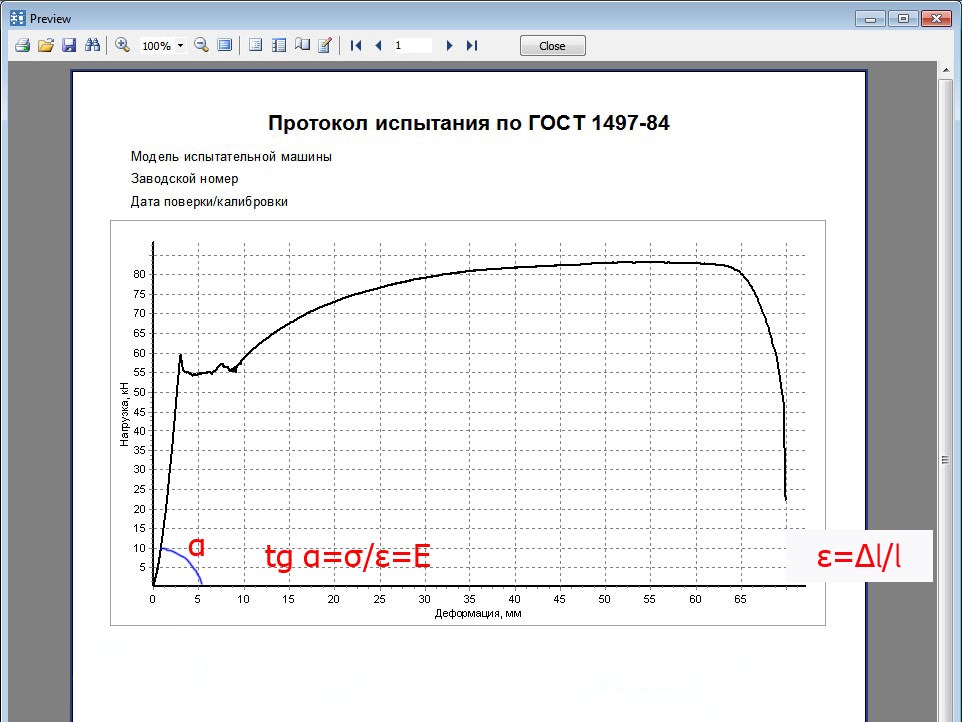
Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.
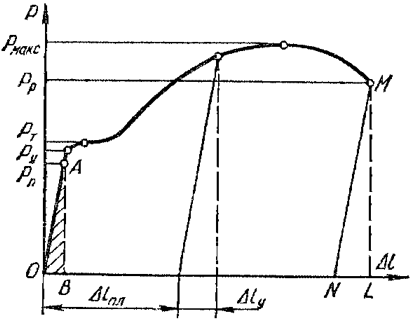
Рисунок 318.1. Диаграмма напряжений для стального образца.
На данной диаграмме мы видим 5 характерных точек:
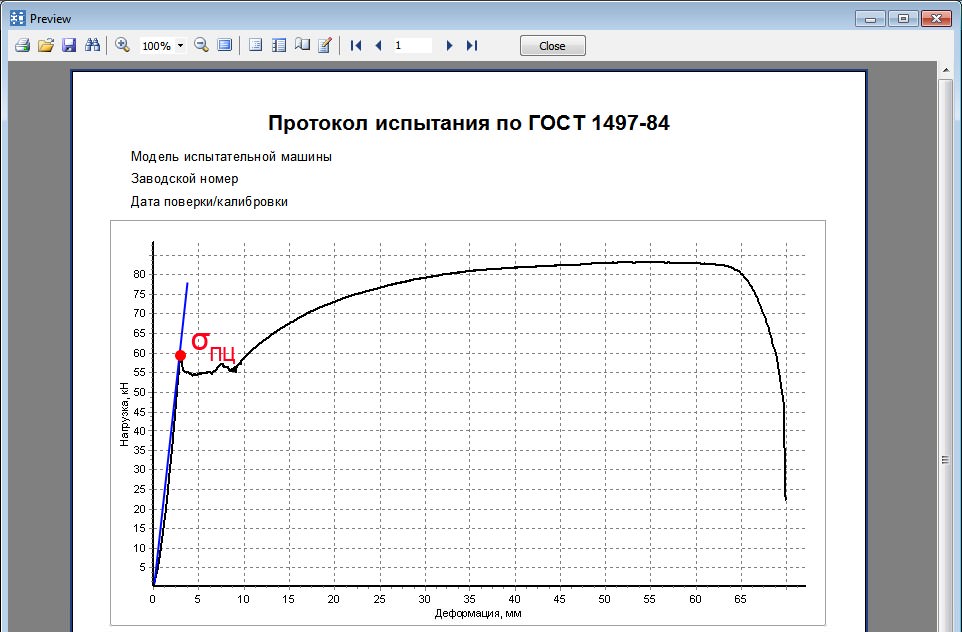
1. Предел пропорциональности Рп (точка А)
Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:
Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:
Рп = kΔl (318.2.2)
k = EF/l (318.2.3)
Модули упругости
Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).
Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности
Модуль Юнга также определяется опытным путем при испытании стандартных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:
σ = Р/Fо (318.3.1), (317.2)
то модуль Юнга согласно закону Гука можно выразить так
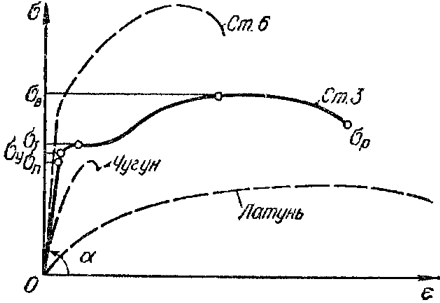
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов
Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным
Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:
Тогда коэффициент Пуассона можно выразить следующим уравнением:
Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига
Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.
т = Р/F (318.3.6)
а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:
tgγ = Δl/h (318.3.7)
то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:
G = т/γ = Ph/FΔl (318.3.8)
Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:
Е = 2(1 + μ)G (318.3.9)
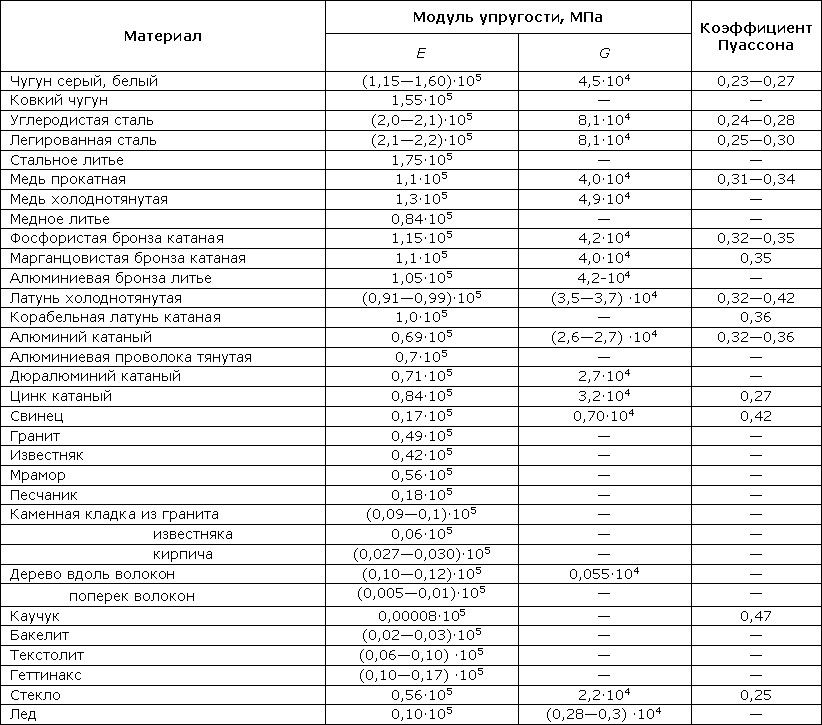
Значения постоянных Е, G и µ приводятся в таблице 318.1
Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов
Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.
Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:
2. Предел упругости Ру
Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:
Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ0.001, σ0.01 и т.д.
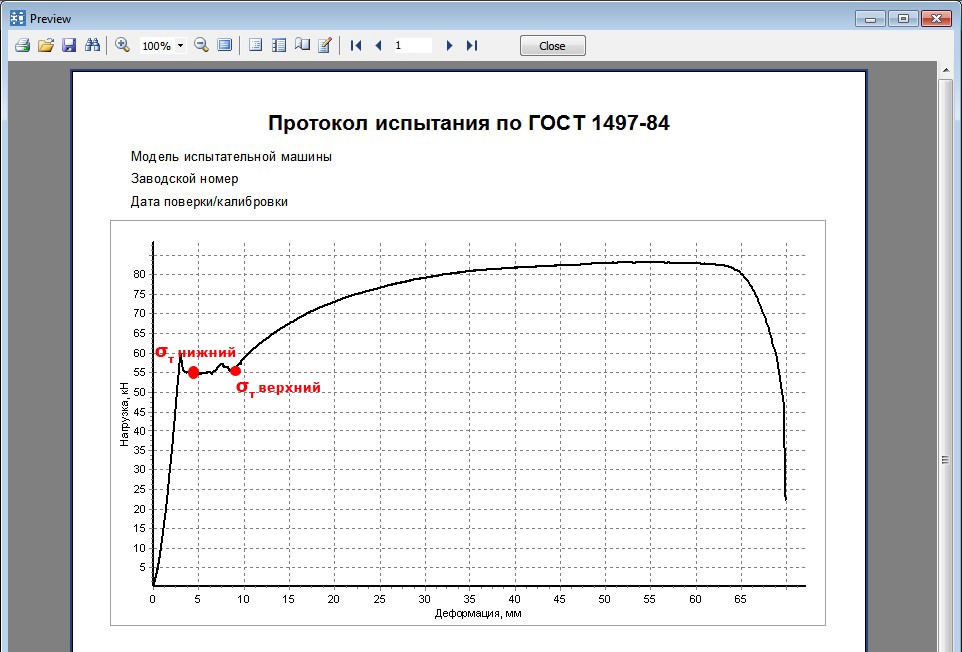
3. Предел текучести Рт
На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.
Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.
4. Предел прочности Рмакс (временное сопротивление)
Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:
После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Рмакс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.
Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.
Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.
Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.
Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс
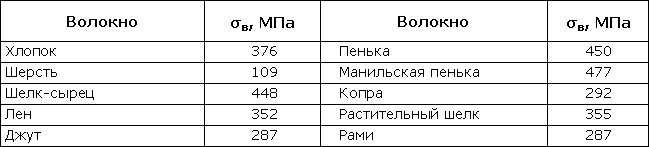
Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон
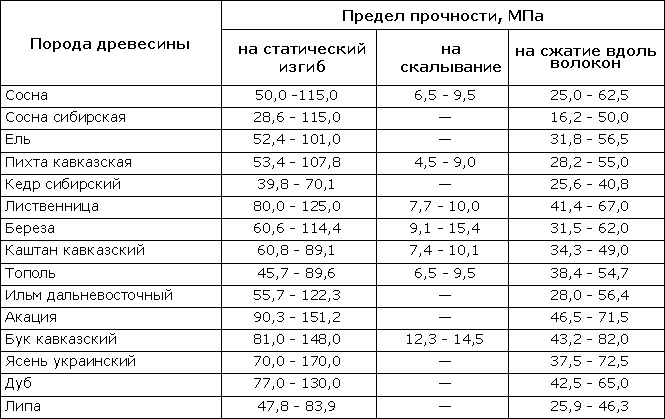
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород
5. Разрушение материала Рр
Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования «шейки» значительно изменяется площадь сечения образца в районе «шейки». Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:
Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.
Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:
Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.
За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:
Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)
Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.
Работа деформации
Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:
А = РΔl/2 (318.4.1)
При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:
А = ηРмаксΔlмакс (318.4.2)
Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.
Деформация сжатия
Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:
Рисунок 318.5
Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.
Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.
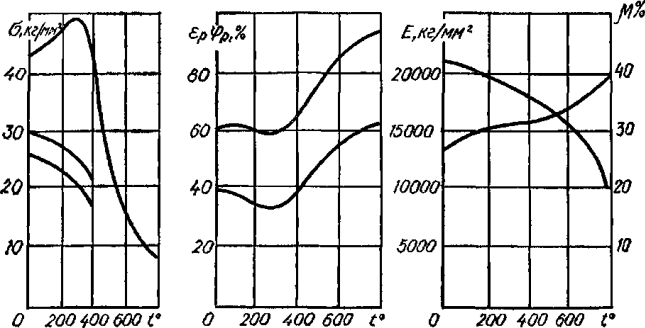
Влияние температуры на изменение механических свойств материалов
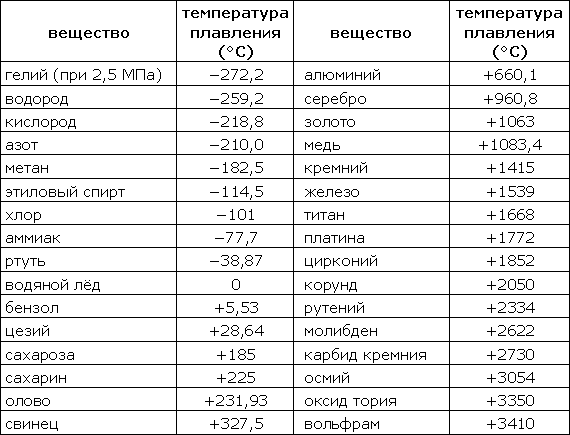
Таблица 318.6. Температуры плавления некоторых веществ
Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).
Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20 о С. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35 о С.
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σп, σт и σв) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.
Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.
При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σв1100 = 2σв20.
Влияние радиоактивного облучения на изменение механических свойств
Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.
Лекция 3. Методики расчета конструкций.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Предел текучести стали
Разные материалы по-разному реагируют на приложенную к ним внешнюю силу, вызывающую изменение их формы и линейных размеров. Такое изменение называют пластической деформация. Если тело после прекращения воздействия самостоятельно восстанавливает первоначальную форму и линейные размеры — такая деформация называется упругой. Упругость, вязкость, прочность и твердость являются основными механическими характеристиками твердых и аморфных тел и обуславливают изменения, происходящие с физическим телом при деформации под действием внешнего усилия и ее предельном случае — разрушении. Предел текучести материала — это значение напряжения (или силы на единицу площади сечения), при котором начинается пластическая деформация.
Текучесть металла
Знание механических свойств материала чрезвычайно важно для конструктора, который использует их в своей работе. Он определяет максимальную нагрузку на ту или иную деталь или конструкцию в целом, при превышении которой начнется пластическая деформация, и конструкция потеряет с вою прочность, форму и может быть разрушена. Разрушение или серьезная деформация строительных конструкций или элементов транспортных систем может привести к масштабным разрушениям, материальным потерям и даже к человеческим жертвам.
Предел текучести — это максимальная нагрузка, которую можно приложить к конструкции без ее деформации и последующего разрушения. Чем выше его значения, тем большие нагрузки конструкция сможет выдержать.
На практике предел текучести металла определяет работоспособность самого материала и изделий, изготовленных из него, под предельными нагрузками. Люди всегда прогнозировали предельные нагрузки, которые могут выдержать возводимые ими строения или создаваемые механизмы. На ранних этапах развития индустрии это определялось опытным путем, и лишь в XIX веке было положено начало созданию теории сопротивления материалов. Вопрос надежности решался созданием многократного запаса по прочности, что вело к утяжелению и удорожанию конструкций. Сегодня необязательно создавать макет изделия определенного масштаба или в натуральную величину и проводить на нем опыты по разрушению под нагрузкой — компьютерные программы семейства CAE (инженерных расчетов) могут с точностью рассчитать прочностные параметры готового изделия и предсказать предельные значения нагрузок.
Величина предела текучести материала
С развитием атомной физики в XX веке появилась возможность рассчитать значение параметра теоретическим путем. Эту работы первым проделал Яков Френкель в 1924 году. Исходя из прочности межатомных связей, он путем сложных для того времени вычислений определил величину напряжения, достаточного для начала пластической деформации тел простой формы. Величина предела текучести материала будет равна
Расчет величины предела текучести
Гениальное допущение, сделанное Френкелем при расчетах, заключалось в том, что процесс изменения формы материала рассматривался как приводимый в действие напряжениями сдвига. Для начала пластической деформации полагалось достаточным, чтобы одна половина тела сдвинулась относительно другой до такой степени, чтобы не смогла вернуться в начальное положение под действием сил упругости.
График физического предела текучести
Френкель предположил, что испытываемый в мысленном эксперименте материал имеет кристаллическое или поликристаллическое строение, свойственно для большей части металлов, керамики и многих полимеров. Такое строение предполагает наличие пространственной решетки, в узлах которой в строго определенном порядке расположены атомы. Конфигурация этой решетки строго индивидуальны для каждого вещества, индивидуальны и межатомные расстояния и связывающие эти атомы силы. Таким образом, чтобы вызвать пластическую деформацию сдвига, потребуется разорвать все межатомные связи, проходящие через условную плоскость, разделяющую половины тела.
При некотором значении напряжения, равному пределу текучести, связи между атомами из разных половин тела разорвутся, и рады атомов сместятся друг относительно друга на одно межатомное расстояние без возможности вернуться в исходное положение. При продолжении воздействия такой микросдвиг будет продолжаться, пока все атомы одной половины тела не потеряют контакт с атомами другой половины
В макромире это вызовет пластическую деформацию, изменит форму тела и при продолжении воздействия приведет к его разрушению. На практике линия начала разрушений проходит не посередине физического тела, а находится в местах расположения неоднородностей материала.
Физический предел текучести
В теории прочности для каждого материала существует несколько значений этой важной характеристики. Физический предел текучести соответствует значению напряжения, при котором, не смотря на деформацию, удельная нагрузка не меняется вовсе или меняется несущественно. Иными словами, это значение напряжения, при котором физическое тело деформируется, «течет», без увеличения прилагаемого к образцу усилия
Условный предел текучести
Большое число металлов и сплавов при испытаниях на разрыв демонстрируют диаграмму текучести с отсутствующей или слабо выраженной «площадкой текучести». Для таких материалов говорят о условном пределе текучести. Его трактуют как напряжение, при котором происходит деформация в переделах 0,2%.
Условный предел текучести
К таким материалам относятся легированные и высокоуглеродистые стальные сплавы, бронза, дюралюминий и многие другие. Чем более пластичным является материал, тем выше для него показатель остаточных деформаций. Примером пластичных материалов могут служить медь, латунь, чистый алюминий и большинство низкоуглеродистых стальных сплавов.
Предел текучести стали
Сталь, как самый популярный массовый конструкционный материал, находится под особо пристальным вниманием специалистов по расчету прочности конструкций и предельно допустимых нагрузок на них.
Стальные сооружения в ходе их эксплуатации подвергаются большим по величине и сложным по форме комбинированным нагрузкам на растяжение, сжатие, изгиб и сдвиг. Нагрузки могут быть динамическими, статическими и периодическими. Несмотря на сложнейшие условия использования, конструктор должен обеспечить у проектируемых им конструкций и механизмов долговечность, безотказность и высокую степень безопасности как для персонала, таки для окружающего населения.
Предел текучести стали
Поэтому к стали и предъявляются повышенные требования по механическим свойствам. С точки зрения экономической эффективности, предприятие стремится снизить сечение и другие размеры производимой им продукции, чтобы снизить материалоемкость и вес и повысить, таким образом, эксплуатационные характеристики. На практике это требование должно быть сбалансировано с требования ми по безопасности и надежности, зафиксированными в стандартах и технических условиях.
Предел текучести для стали является ключевым параметрам в этих расчетах, поскольку он характеризует способность конструкции выдерживать напряжения без необратимых деформаций и разрушения.
Влияние содержание углерода на свойства сталей
Согласно физико-химическому принципу аддитивности, изменение физических свойств материалов определяется процентным содержанием углерода. Повышение его доли до 1,2% дает возможности увеличить прочность, твердость, предел текучести и пороговую хладоемкость сплава. Дальнейшее повышение доли углерода приводит к заметному снижению таких технических показателей, как способность к свариваемости и предельная деформация при штамповочных работах. Стали с низким содержанием углерода демонстрируют наилучшую свариваемость.
Азот и кислород в сплаве
Эти неметаллы из начала таблицы Менделеева являются вредными примесями и снижают механические и физические характеристики стали, такие, например, как порог вязкости, пластичность и хрупкость. Если кислород содержится в количестве свыше 0,03%- это ведет к ускорению старения сплава, а азот увеличивает ломкость материала. С другой стороны, содержание азота повышает прочность, снижая предел текучести.
Микроструктура сплава, в составе которого присутствуют азот и кислород
Добавки марганца и кремния
Легирующая добавка в виде марганца применяется для раскисления сплава и компенсации отрицательного влияния вредных серосодержащих примесей. Ввиду своей близости по свойствам к железу существенного самостоятельного влияния на свойства сплава марганец не оказывает. Типовое содержание марганца – около 0,8%.
Кремний оказывает похожее воздействие, его добавляют в процессе раскисления в объемной доле, не превышающей 0,4%. Поскольку кремний существенно ухудшает такой технический показатель, как свариваемость стали. Для конструкционных сталей, предназначенных для соединения сваркой, его доля не должна превышать 0,25%. На свойства стальных сплавов кремний влияния не оказывает.
Примеси серы и фосфора
Сера является исключительно вредной примесью и отрицательно воздействует на многие физические свойства и технические характеристики.
Предельно допустимое содержание этого элемента в виде хрупких сульфитов– 0,06%
Сера ухудшает пластичность, предел текучести, ударную вязкость, износостойкость и коррозионную стойкость материалов.
Фосфор оказывает двоякое воздействие на физико-механические свойства сталей. С одной стороны, с повышением его содержания повышается предел текучести, однако с другой стороны, одновременно понижаются вязкость и текучесть. Обычно содержание фосфора находится в пределах от 0,025 до 0,044%. Особенно сильное отрицательное влияние фосфор оказывает при одновременном повышении объемных долей углерода.
Легирующие добавки в составе сплавов
Легирующими добавками называют вещества, намеренно введенные в состав сплав для целенаправленного изменения его свойств до нужных показателей. Такие сплавы называют легированными сталями. Лучших показателей можно добиться, добавляя одновременно несколько присадок в определенных пропорциях.
Влияние легирующих элементов на свойства стали
Распространенными присадками являются никель, ванадий, хром, молибден и другие. С помощью легирующих присадок улучшают значение предела текучести, прочности, вязкости, коррозионной стойкости и многих других физико-механических и химических параметров и свойств.
Текучесть расплава металла
Текучестью расплава металла называют его свойство полностью заполнять литейную форму, проникая в малейшие полости и детали рельефа. От этого зависит точность отливки и качество ее поверхности.
Жидкий металл для процессоров
Свойство можно усилить, если поместить расплав под избыточное давление. Это физическое явление используется в установках литья под давлением. Такой метод позволяет существенно повысить производительность процесса литья, улучшить качество поверхности и однородность отливок.
Испытание образца для определения предела текучести
Чтобы провести стандартные испытания, используют цилиндрический образец диаметром 20 мм и высотой 10 мм, закрепляют его в испытательной установке и подвергают растягиванию. Расстояние между нанесенными на боковой поверхности образца метками называют расчетной длиной. В ходе измерений фиксируют зависимость относительного удлинения образца от величины растягивающего усилия.
Зависимость отображают в виде диаграммы условного растяжения. На первом этапе эксперимента рост силы вызывает пропорциональное увеличение длины образца. По достижении предела пропорциональности диаграмма из линейной превращается в криволинейную, теряется линейная зависимость между силой и удлинением. На этом участке диаграммы образец при снятии усилия еще может вернуться к исходным форме и габаритам.
Для большинства материалов значения предела пропорциональности и предела текучести настолько близки, что в практических применениях разницу между ними не учитывают.