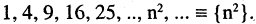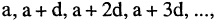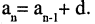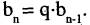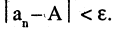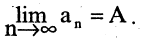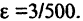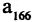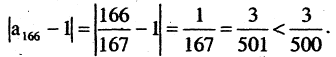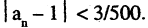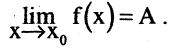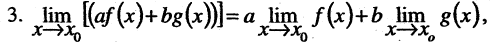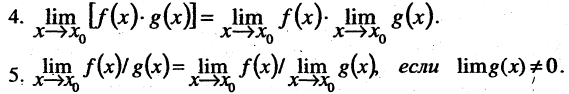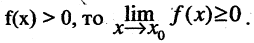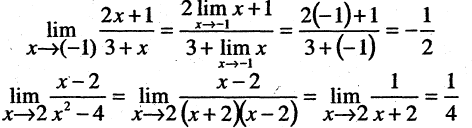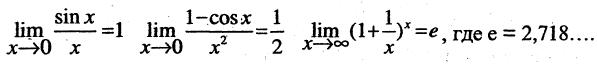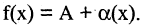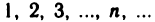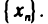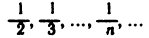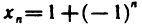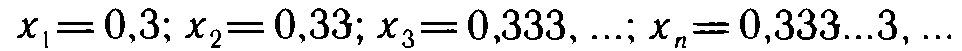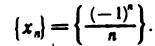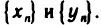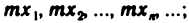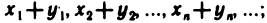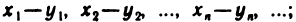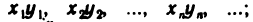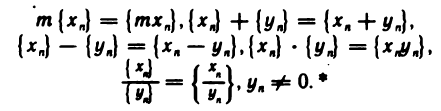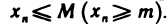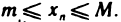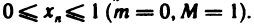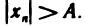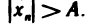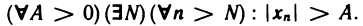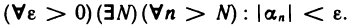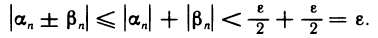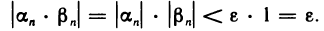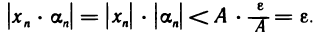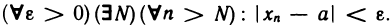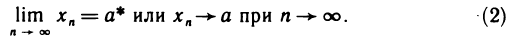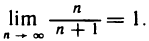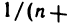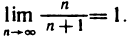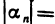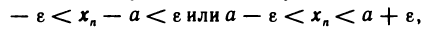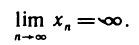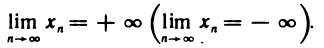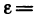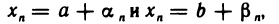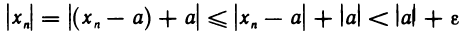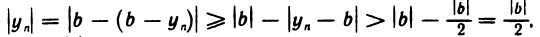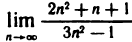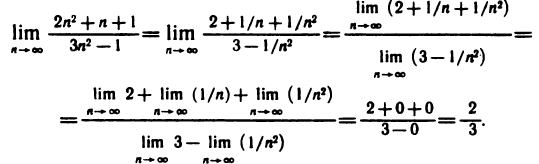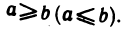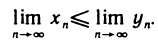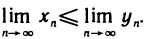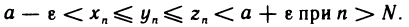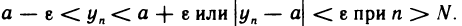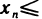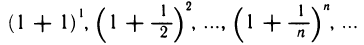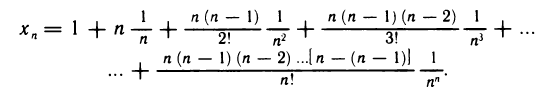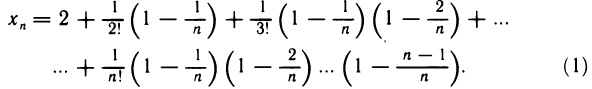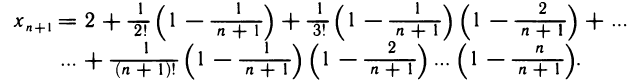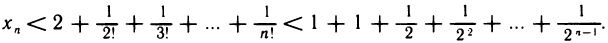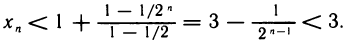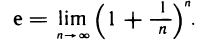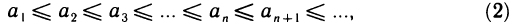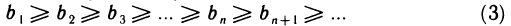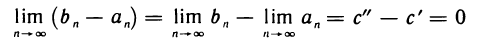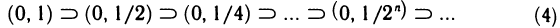Что называется пределом последовательности
Предел последовательности в математике с примерами решения и образцами выполнения
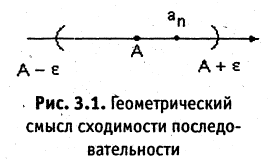
Предел последовательности — это пространство которое содержит все все элементы последовательности начиная с какого-то значения. А простыми словами, предел последовательности, простыми словами, это такая «область» куда попадают все значения после определенного порога (в нашем случае – А). На изображении ниже она условно показана синей полоской.
Понятие предела и понятие функции — фундаментальные понятия математического анализа. Начало изучению понятия предела положено в элементарной математике, где с помощью предельных переходов определяются длина окружности, объем цилиндра, конуса и т. д. Оно также было использовано при определении суммы бесконечно убывающей геометрической прогрессии. Операция предельного перехода является одной из основных операций анализа. В настоящей главе рассматривается простейшая форма операции предельного перехода, основанная на понятии предела числовой последовательности. Понятие предела числовой последовательности позволит в дальнейшем определить и другие более сложные формы операции предельного перехода.
Предел числовой последовательности:
Числовую функцию 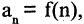
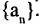
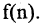
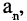
Если закон, по которому задается последовательность, позволяет построить очередной член последовательности по известным предыдущим членам, то такой способ задания называется рекуррентным. Например, арифметическая последовательность (арифметическая прогрессия) 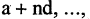
Геометрическая последовательность (геометрическая прогрессия) 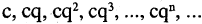
Кроме рекуррентного соотношения, задаются также первые члены последовательности, и, возможно, некоторые параметры. Так для арифметической и геометрической последовательностей достаточно задать лишь их первые члены а и b, а также и параметры прогрессий d и q соответственно.
Последовательность называется ограниченной сверху, если существует число М (верхняя граница), такое, что, 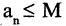
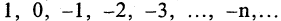
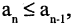
Последовательность 
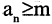
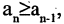
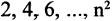
Последовательность 
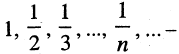
Сходимость последовательности. Последовательность 
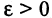
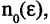
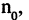
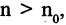
Этот факт записывается так:
Само число А называется пределом последовательности 
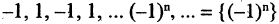
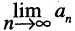
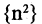
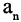
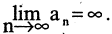
Если последовательность имеет пределом точку А, то для всех номеров последовательности, начиная с некоторого 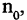
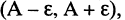
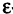
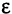
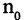
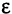
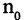
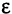
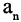
Пример:
Рассмотрим последовательность 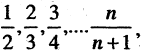
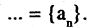
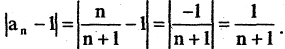
Вычислим отклонение для
Тем самым, начиная с 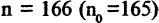
Предел функции:
Пусть 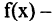
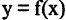
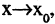
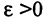
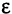
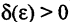
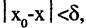
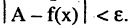
Наличие у функции 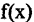



Справедливы следующие свойства пределов функций:
1.Если предел функции существует, то он единственный.
2.Предел постоянной величины равен самой постоянной.
Если при 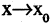
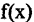
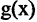
6.Если 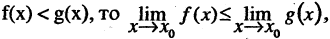
В качестве примера вычислим два предела.
На практике при вычислении пределов часто используют так называемые замечательные пределы
Бесконечно малые и бесконечно большие величины:
Если при 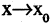
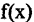
окрестности точки 
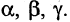
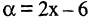
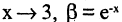
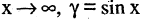
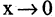
1.Сумма бесконечно малых величин есть величина бесконечно малая.
2.Произведение бесконечно малых величин есть величина бесконечно-малая.
3.Произведение бесконечно малой на число есть величина бесконечно малая.
4.Разность между функцией и ее пределом в точке а есть величина бесконечно малая, т. е., если 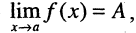
Функция называется бесконечно большой величиной в окрестности точки 
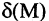

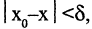
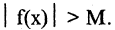
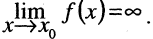
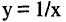
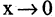
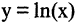
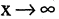
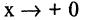
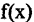
Замечание:
Бесконечность (обозначаемая знаком 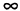
Функция 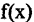

Точки, в которых равенство (3.1) не выполняется, называются точками разрыва функции. Функция непрерывна на промежутке, если она непрерывна в каждой точке промежутка. Непрерывные функции обладают рядом свойств.
Все элементарные функции, а также любая их суперпозиция непрерывны в своей области определения.
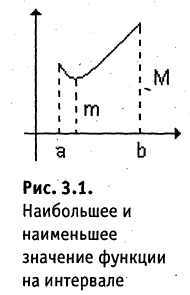
Если функция непрерывна на замкнутом промежутке [а, b], то она достигает на этом промежутке наибольшего М и наименьшего m значений (рис. 3.2).
Числовые последовательности
Числовые последовательности и арифметические действия над ними. Числовые последовательности изучают уже в средней школе. Примерами таких последовательностей могут служить: 1) последовательность всех членов арифметической и геометрической прогрессий; 2) последовательность периметров правильных л-угольников, вписанных в данную окружность; 3) последовательность 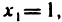
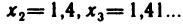
Уточним и расширим понятие числовой последовательности.
Определение:
Если каждому числу п из натурального ряда чисел
поставлено в соответствие вещественное число 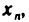
называется числовой последовательностью или просто последовательностью*
Числа 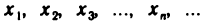
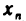
Так, например, символ 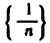
Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула
*Другими словами, числовую последовательность можно определить как множество пар чисел, в которых первое число принимает последовательно значения 1, 2, 3, … задает последовательность: 0,2, 0,2, … Обращая дробь 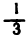
По самому определению, последовательность содержит бесконечное число элементов: любые два ее элемента отличаются, по крайней мере, своими номерами.
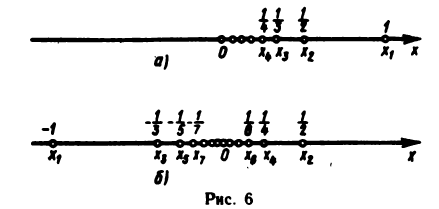
Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. На рис. 6, а
и б изображены соответственно последовательности 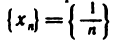
Введем арифметические действия над числовыми последовательностями. Пусть даны последовательности
Произведением последовательности 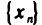
суммой данных последовательностей назовем последовательность
разностью — последовательность
произведением — последовательность
частным — последовательность 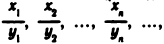
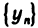
Указанные действия над последовательностями символически записываются так:
Ограниченные и неограниченные последовательности
Определение:
Последовательность 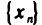
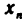
Определение:
Последовательность 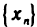
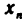
Пусть 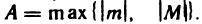
Определение:
Последовательность 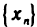
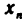
Из данных определений следует, что если последовательность ограничена сверху, то все ее элементы принадлежат промежутку 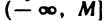
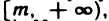
Рассмотрим примеры ограниченных и неограниченных последовательностей.
1. Последовательность 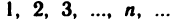
2. Последовательность 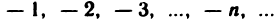
3. Последовательность 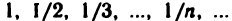
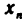
4. Последовательность 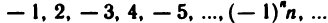
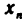
С помощью логических символов данные выше определения можно записать следующим образом:
Сравнивая запись с помощью логических символов двух последних определений, видим, что при построении отрицаний символы 
Бесконечно большие и бесконечно малые последовательности
Определение:
Последовательность 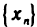

Символическая запись определения бесконечно большой последовательности:
Замечание:
Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограничен-ная последовательность может и не быть бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3, …, 1, n, 1, n+1… не является бесконечно большой, поскольку при A > 1 неравенство 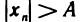
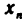
Определение:
Последовательность 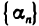
Символическая запись определения бесконечно малой последовательности:
Пример:
Используя определение 1, докажем, что последовательность 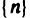
Возьмем любое число A>0. Из неравенства 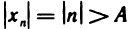
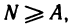

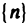
Пример:
Используя определение 2, докажем, что последовательность [1 /n] является бесконечной малой.
Возьмем любое число 
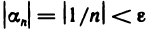
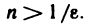
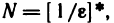
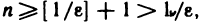
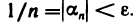
Докажем теорему, устанавливающую связь между бесконечно большими и бесконечно малыми последовательностями.
Теорема:
Если 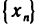
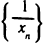
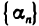
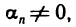
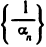
Доказательство:
Пусть 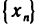
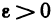
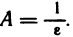
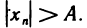
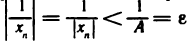
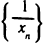
Доказательство второй части теоремы проводится аналогично.
Основные свойства бесконечно малых последовательностей
Теорема:
Сумма и разность двух бесконечно малых последовательностей есть бесконечно малые последовательности.
Доказательство:
Пусть 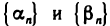
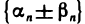
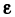
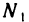
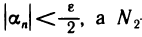
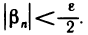
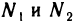
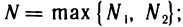
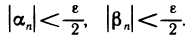
Это значит, что последовательность 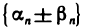
Следствие:
Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема:
Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство:
Пусть 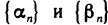
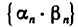
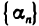

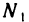
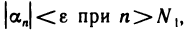
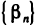
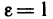
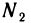
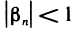

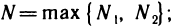
Это означает, что последовательность 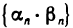
Следствие:
Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Замечание:
Частное двух бесконечно малых последовательностей может не быть бесконечно малой последовательностью и может даже не иметь смысла. Например, если 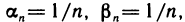
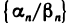
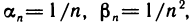
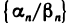
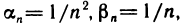
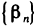
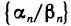
Теорема:
Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.
Доказательство:
Пусть 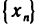
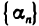
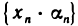
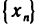
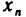
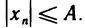

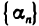
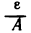
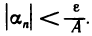
Это означает, что последовательность 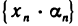
Следствие:
Произведение бесконечно малой последовательности на число есть бесконечно малая последовательность.
Перейдем теперь к одному из важнейших в математическом анализе понятию предела числовой последовательности.
Сходящиеся последовательности
Понятие сходящейся последовательности и её определение:
Число а называется пределом последовательности 
С помощью логических символов это определение можно записать в виде
Последовательность, имеющая предел, называется сходящейся.
Если последовательность 
Последовательность, не являющаяся сходящейся, называется pасходящейся.
Пример:
Используя определение предела последоватeльности. Докажем, что
Возьмем любое число е>0. Так как 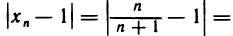
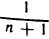
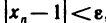

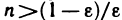
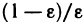
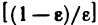
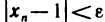
Замечание:
Пусть последовательность 
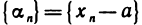
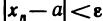
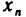
где 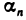
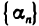
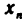
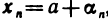
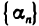
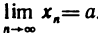
Замечание:
Неравенство (1) равносильно неравенствам
которые означают, что элемент 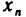

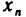
Замечание:
Очевидно, что бесконечно большая последовательность 
Если при этом, начиная с некоторого номера, все члены последовательности положительны (отрицательны), то пишут
Предел последовательности, как он был определен ранее, будем называть иногда в отличие от бесконечного предела конечным пределом.
Замечание:
Очевидно, всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число а=0.
2. Основные свойства сходящихся последовательностей. Докажем лемму, которая понадобится при доказательстве теоремы 2.5.
Лемма:
Если все элементы бесконечно малой последовательности 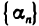
Доказательство:
Предположим противное, т. е. что с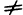
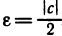
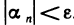
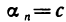
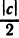
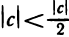
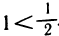
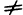
Теорема:
Сходящаяся последовательность имеет только один предел.
Доказательство:
Предположим противное, т. е. что сходящаяся последовательность 
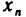
где 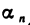
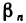
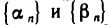
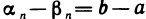
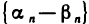
Теорема:
Сходящаяся последовательность ограничена.
Доказательство:
Пусть 
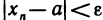
для всех n>N. Пусть 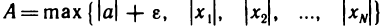
Очевидно, 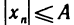

Замечание:
Ограниченная последовательность может и не быть сходящейся. Например, последовательность —1, 1, —1, …, 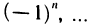
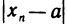
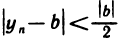
т. е. 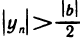
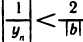
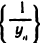
По теореме 2.4 последовательность 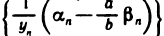
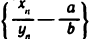
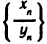
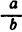
Теоремы, доказанные в этом пункте, имеют большое не только теоретическое, но и практическое значение.
Пример:
Найдем
При 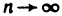
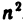
Предельный переход в неравенствах. Теорема 2.10.
Если элементы сходящейся последовательности 
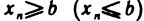
Доказательство:
Пусть все элементы 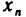
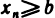
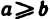
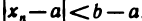

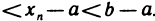

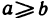

Следствие:
Если элементы сходящихся последовательностей 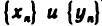
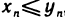
В самом деле, начиная с некоторого номера, элементы последовательности 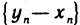
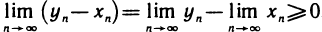
Следствие:
Если все элементы сходящейся последовательности 
В самом деле, так как 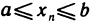
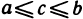
Теорема:
Пусть даны три последовательности 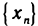
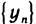
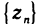
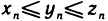
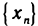
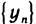
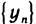
Доказательство:
Возьмем любое е>0. По этому е для последовательности 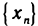
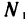
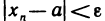

По тому же е для последовательности 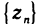
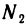
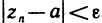
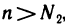
Пусть 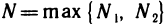
Это означает, что предел последовательности 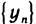
Монотонные последовательности
Определение и признак сходимости монотонных последовательностей. Определение. Последовательность 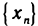
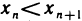
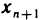

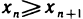
Все такие последовательности объединяются общим названием: монотонные последовательности. Возрастающие и убывающие последовательности называются также строго монотонными.
Рассмотрим примеры монотонных последовательностей.
Отметим, что монотонные последовательности ограничены, по крайней мере, с одной стороны: неубывающие последовательности—снизу ( 
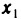
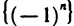
Имеет место следующая основная теорема о монотонных последовательностях.
Теорема:
Монотонная ограниченная последовательность сходится.
Доказательство:
Рассмотрим случай неубывающей последовательности.
Так как а — точная верхняя грань множества элементов последовательности 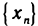
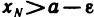
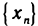
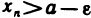

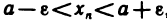
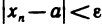
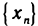
Случай невозрастающей последовательности рассматривается аналогично.
Замечание:
Ограниченность монотонной последовательности является необходимым и достаточным условием сходимости.
В самом деле, если монотонная последовательность ограничена, то в силу теоремы 2.12 она сходится; если же монотонная последовательность сходится, то по теореме 2.6 она ограничена.
2.Число е. Рассмотрим последовательность 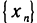
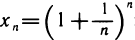
Докажем, что она сходится. Для этого достаточно доказать, что последовательность 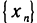
Представим это выражение в следующей форме:
Аналогичным образом представим 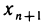
Заметим теперь, что 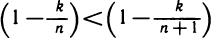
Используя формулу суммы геометрической прогрессии, придем к неравенству
Таким образом, доказано, что последовательность 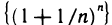
Отметим, что число е играет большую роль во многих вопросах математики. Оно, в частности, является основанием натуральных логарифмов. В настоящем параграфе дано только определение числа е. Далее будет рассмотрен способ вычисления этого числа с любой степенью точности.
Здесь лишь отметим, что так как 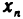
Пусть дана последовательность отрезков 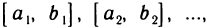
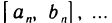
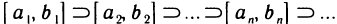

и пусть 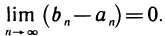
Теорема:
Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности.
Доказательство:
Из неравенств (1) следует, что левые концы отрезков образуют неубывающую последовательность
а правые концы — невозрастающую последовательность
При этом последовательность (2) ограничена сверху, а последовательность (3) ограничена снизу, так как 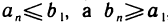
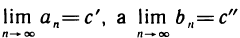
следует, что с’ = с», т. е. последовательности 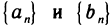
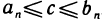
Докажем теперь, что такая точка только одна. Допустим, что существует еще одна точка 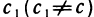
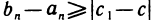
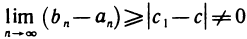
Замечание. Теорема неверна, если вместо отрезков рассматривать интервалы. Например, для последовательности вложенных интервалов
не существует точки, принадлежащей всем интервалам. В самом деле, какую бы точку с на интервале (0, 1) ни взять, всегда найдется номер N такой, что при n>N будет 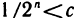
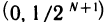
Для дальнейшего изложения нам понадобятся некоторые сведения из аналитической геометрии. Поэтому следующая глава посвящена этому разделу математики.
Дополнение к пределу последовательности



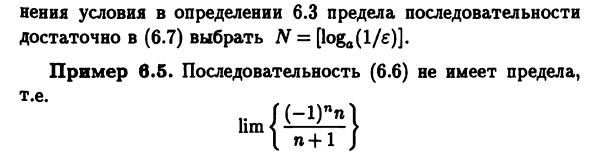
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института