Что называется полной группой событий
Полная группа событий
По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.
Определение
Пусть 


Пример
Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:
Таким образом, система 
Полезное
Смотреть что такое «Полная группа событий» в других словарях:
Группа Дятлова — Гибель тургруппы Дятлова событие, случившееся в ночь с 1 на 2 февраля 1959 года на Северном Урале, когда при загадочных обстоятельствах погибла группа туристов, возглавляемая Игорем Дятловым. Причина гибели не ясна до сих пор. Перевал, рядом с… … Википедия
Сплин (группа) — Сплин Основная информация Жанр … Википедия
Машина времени (группа) — У этого термина существуют и другие значения, см. Машина времени (значения). Машина времени … Википедия
Инь-Ян (группа) — Эта статья о группе. О взаимодействии крайних противоположностей см. Инь Ян. Инь Ян Жанры поп музыка Годы 25 ноября 2007 по … Википедия
Последовательность событий 11 сентября 2001 года — Здесь приведена хронология теракта 11.09.01, в котором самолёт разрушил одну из башен близнецов торгового центра в Нью Йорке. Дано местное Нью Йоркское время. Содержание 1 События 1.1 6:00 AM 1.2 7:00 AM 1.3 8:00 AM 1.4 9:00 AM … Википедия
Хронология событий 11 сентября 2001 года — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Здесь приведен … Википедия
Случайное событие — Случайное событие подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в… … Википедия
Террористические акты 11 сентября 2001 года — Террористические акты 11 сентября 2001 года … Википедия
Понятие полной группы событий



— любые два события из рассматриваемого множества событий – несовместны
— в результате испытания одно из событий обязательно произойдет.
1) события выпадения очков от 1 до 6 при одном бросании
2) орла и решки и другие.
Используя понятие полной группы событий, можно дать следующее определение противоположного события: два единственно возможных несовместных события образуют полную группу: A и Ā:
А – попадание в цель
2.3. Операции над событиями (результат – событие!)
• Ā противоположное событие – наступает во всех остальных случаях, кроме A. Аналогии: вычитание множеств и операция отрицания в логике ( «не» А)
 |
Например, шарики, вытаскиваем два. События A: первый шарик – белый, B: второй шарик – белый:
• A+B хотя бы один белый
К результатам операций, которые являются событиями, возможно применение операций над событиями, поэтому допустимы выражения, например, 
Полная группа событий
Сумма вероятностей всех событий в группе всегда равна 1.
Связанные понятия
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
В теории вероятностей говорят, что событие почти достоверно или что оно произойдет почти наверняка, если это произойдет с вероятностью 1. Понятие является аналогом понятия «почти всюду» в теории меры. В то время, как во многих основных вероятностных экспериментах нет никакой разницы между «почти достоверно» и «достоверно», (то есть, событие произойдет совершенно точно), это различие важно в более сложных случаях, относящихся к случаям рассмотрения какой-либо бесконечности. Например, термин часто.
Случайность имеет множество применений в области науки, искусства, статистики, криптографии, игр, азартных игр, и других областях. Например, случайное распределение в рандомизированных контролируемых исследованиях помогает ученым проверять гипотезы, а также случайные и псевдослучайные числа находят применение в видео-играх, таких как видеопокер.
В математике теория момента остановки или марковский момент времени связана с проблемой выбора времени, чтобы принять определённое действие, для того чтобы максимизировать ожидаемое вознаграждение или минимизировать ожидаемые затраты. Проблема момента остановки может быть найдена в области статистики, экономики и финансовой математики (связанные с ценообразованием на американские опционы). Самым ярким примером, относящимся к моменту остановки, является Задача о разборчивой невесте. Проблема момента.
Полная группа событий



Доказательство:
Противоположными событиями являются например, выпадение герба и выпадение цифры при бросании монеты; попадание и промах при стрельбе в цель; событие «день дождливый» и «день ясный»; события «3 дня подряд шел снег» и » хотя бы в один из 3-х дней снега не было».
Следствие: Сумма вероятностей противоположных событий равна 1.
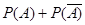
Переход к противоположному событию нередко облегчает вычисление вероятности. На практике весьма часто оказывается легче вычислить вероятность противоположного события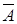
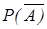
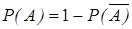
Вероятности противоположных событий принято обозначать p и q, следовательно p+q=1.
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
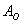
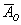
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
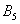
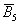
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
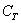
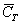
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 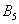
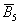
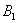
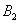
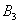
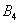
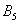
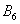
События 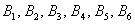
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 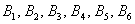
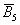
В примере с картами события 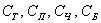
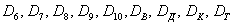
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
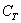
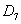
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
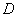
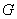
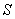
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин




