Что называется погрешностью округления определение
Ошибки вычислений
Материал из MachineLearning.
Содержание
Введение
Постановка вопроса. Виды погрешностей
Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.
При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.
Виды мер точности
Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой
В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:
Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:
Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.
Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений
Предельные погрешности
Можно показать, что при малых эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой
Несложно показать, что:
Погрешности округлений при представлении чисел в компьютере
Абсолютная погрешность округления в этом случае равна
Погрешности арифметических операций
При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.
Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).
Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.
Если сумма точных чисел равна
сумма приближенных чисел равна
Относительная погрешность суммы нескольких чисел равна
Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
0.» alt= «min \quad \delta(a_k)\le\delta(S)\le max \quad \delta(a_k), \qquad k=1,2. n, \quad a_k>0.» />
При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.
Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.
При другой последовательности действий погрешность будет другой:
Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:
При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.
При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:
где – суммарная погрешность, – погрешность выполнения операций с плавающей точкой,
– погрешность представления чисел с плавающей точкой.
Погрешности вычисления функций
(погрешностью других аргументов пренебрегаем).
Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:
Числовые примеры
Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.
ПРИМЕР 1. Вычислить все корни уравнения
Точное решение задачи легко найти:
ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:
Общее решение имеет вид:
ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:
Соответственно, разность будет:
Таким образом, требование к заданию точности начальных данных оказываются в раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.
Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.
В памяти машины эти же числа представляются в виде:
Относительная ошибка при вычислении разности будет равна:
ПРИМЕР 6. Рассмотрим рекуррентное соотношение 0, \quad u_i > 0.» alt= «u_
Следовательно, если 1″ alt= «|q| > 1» />, то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае погрешность не возрастает и численный алгоритм устойчив.
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
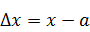
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
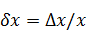
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

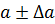
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 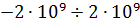
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
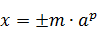
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 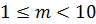
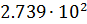
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 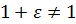
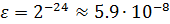
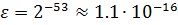
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
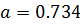
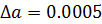
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
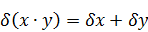
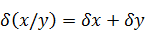
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
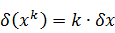
При сложении или вычитании чисел их абсолютные погрешности складываются:
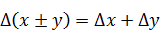
Относительная погрешность суммы положительных слагаемых вычисляется как:
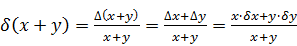
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
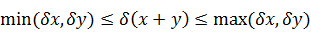
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 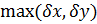
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 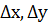
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Обработка результатов измерений и определение погрешностей измерений (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 |
4. ПРАВИЛА ОКРУГЛЕНИЯ ПРИБЛИЖЕННЫХ ЧИСЕЛ
Незначащими цифрами числа называются нули в начале десятичных дробей, меньших 1, и нули в конце числа, заменившие цифры, отброшенные после округления. Остальные цифры называются значащими.
Сомнительной цифрой результата измерения называется цифра, стоящая в разряде, соответствующем старшему разряду со значащей цифрой в значении погрешности. Цифры, стоящие слева от сомнительной называются верными, а справа – неверными.
Пример. Числа 586 ± 6; 0,00234 ± 0,00002; 1,00 ± 0,03; 2000 ± 30 содержат по три значащие цифры. При округлении числа 299793 ± 1 до значения 3 × 105 допущена погрешность 207, поэтому в полученном числе сотни являются сомнительной цифрой и, следовательно, последние два нуля – незначащие.
Погрешность обычно выражается одной значащей цифрой и лишь при особо ответственных измерениях – двумя.
4.1.Округление погрешности действительного значения
Погрешность округляется до одной значащей цифры. Эта цифра является сомнительной т. к. значение погрешности не имеет верных цифр.
Действительное значение округляется до цифры, разряд которой равен разряду значений цифры погрешности. Последняя цифра действительного значения – сомнительная, остальные цифры – верные.
При особо точных измерениях погрешность округляется до двух значащих цифр, если первая из них меньше 4-х и до одной цифры, если первая цифра больше 3-х. Иногда в качестве второй цифры оставляют 0 или 5.
4.2. Запись чисел, считанных со шкалы прибора
В числовом значении измеряемой величины, считанном со шкалы прибора, записываются только верные цифры и сомнительная цифра, разряд которой определяется по значению инструментальной погрешности прибора.
4.3. Округление чисел
Лишние цифры у целых чисел заменяются нулями, а у десятичных дробей отбрасываются. Если заменяемая нулем или отбрасываемая цифра старшего разряда меньше 5, то оставшиеся цифры не изменяются. Если указанная цифра больше 5, то последняя оставшаяся цифра увеличивается на 1. Если заменяемая нулем или отбрасываемая цифра равна 5, то округление производится следующим образом: последняя цифра в округленном числе остается без изменения, если она четная, и увеличивается на 1, если она нечетная.
4.4. Округление при вычислениях
При записи результатов промежуточных вычислений сохраняется одна запасная цифра – цифра, стоящая справа от сомнительной. При сложении, вычитании приближенных чисел разряд сомнительной цифры результата совпадает со старшим из разрядов сомнительных цифр слагаемых. Результат умножения и деления содержит столько значащих цифр, сколько их в исходном данном с наименьшим количеством значащих цифр. При возведении в степень (извлечении корня) приближенного числа результат должен иметь столько цифр, сколько их в основании (подкоренном выражении). При логарифмировании в мантиссе сохраняется столько значащих цифр, сколько их в исходном числе. Если один из операндов – точное число, то количество его цифр не влияет на округление результата операции. Если при вычислениях используются табличные данные, то все их цифры верные.
Приведем примеры округления результатов измерения.
Погрешность округления. Полная погрешность прямого измерения



Как уже говорилось выше, на измеренное значение физической величины влияют случайные и систематические ошибки, в частности ошибки измерительного прибора. Очевидно, эти факторы необходимо учитывать и при вычислении полной погрешности прямого измерения.
Кроме случайной погрешности и погрешности прибора необходимо учитывать и погрешность округления. Это погрешности связанные дискретностью шкалы или индикации измерительного прибора и необходимостью округления промежуточного значения (между соседними рисками шкалы или значениями цифрового индикатора).
Интервал округления h может быть различным. Если отсчет снимается с точностью до целого деления, то интервал округления равен цене деления шкалы прибора (дискрету младшего знака индикатора). Если отсчет округляется до половины деления, интервал округления равен половине цены деления и т.д. Максимальная погрешность округления, очевидно, не превышает половины интервала округления т.е. величин h/2.
Для доверительной вероятности Р можно записать выражение абсолютной погрешности округления
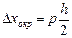
Пример. Пусть значение тока в цепи, измеренное при помощи амперметра равно I. Шкала прибора имеет деление ценой 0,1 мА. Отсчет округляется до одного деления, т.е. до 0,1 мА. Значит, величина h=0,1 мА, а абсолютная погрешность округления
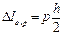
Градуировка измерительных приборов обычно производится так, чтобы деление шкалы было в интервале [δ; 2δ]. Тогда при округлении до половины деления (наиболее удобном) Δxокр будет вдвое меньше приборной погрешности δ и поэтому ее вклад в полную погрешность несущественен. Отсюда можно вывести весьма полезное правило: если не известна погрешность измерительного прибора, то ее можно оценочно принять равной половине цены деления шкалы. Правило справедливо если прибор не перестраивали после изготовления с помощью дополнительного сопротивления или шунта.
В теории вероятностей показывается, что погрешность, обусловленная несколькими независимыми факторами, определяется квадратичным суммированием. Поскольку в лабораторных учитываются сразу три погрешности, то полная абсолютная погрешность прямого измерения
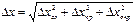
а относительная погрешность
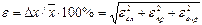
При вычислении всех суммируемых погрешностей доверительная вероятность Р выбирается одинаковой (например, р=0,95). Такой же оно будет и для полной погрешности. Если какая-либо из погрешностей раза в три меньше любой другой, ее вклад в полную погрешность незначителен и ею можно пренебречь.
Рассмотрим на конкретном примере полную обработку результатов прямых измерений.
Пример. Пусть измеряется э.д.с. датчика Холла. Контрольное наблюдение показало, что U 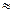
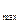
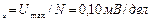
Первые три измерения показали, что в опыте появляется разброс данных, обусловленный случайными ошибками. Поэтому количество наблюдений увеличено до десяти. Полученные результаты приведены в таблице 1.3.
| Номер наблюдения | U | ΔU | Номер наблюдения | U | ΔU |
| мВ | мВ | мВ | мВ | ||
| 12,05 | -0,065 | 12,10 | -0,015 | ||
| 12,20 | +0,085 | 12,00 | -0,115 | ||
| 12,10 | -0,015 | 12,15 | +0,035 | ||
| 12,05 | -0,065 | 12,10 | -0,015 | ||
| 12,15 | +0,035 | 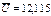 | 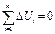 | ||
| 12,25 | +0,135 |
1. Рассчитать среднее арифметическое 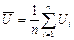
2. Определить случайные отклонения 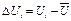
3. Проверить равенство нулю алгебраической суммы всех значений ΔU.
4. Рассчитать случайную погрешность (при Р=0,95).
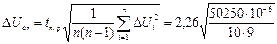
5. Определить приборную погрешность измерения.
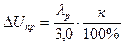
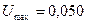
6. Найти погрешность округления (интервал округления h=0,05 мВ).
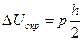
7. Определить полную погрешность измерения.
8. Вычислить относительную погрешность измерения.
9. Найти поправку на систематическую погрешность метода: вольтметр измеряет не ЭДС, а напряжение. Поэтому необходимо учитывать падение напряжения на нем самом. С учетом закона Ома систематическая ошибка 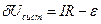
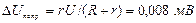
Поправка на порядок меньше полной погрешности, поэтому ею можно пренебречь.
10. Записать окончательный результат

В заключение этого раздела несколько слов о количестве повторных наблюдений. Как следует из (1.10), большое количество наблюдений позволит уменьшать случайную погрешность. Однако, это требует дополнительных затрат времени, труда, энергии и т.д. Поэтому вопрос о количестве наблюдений должен быть обдуман и обоснован (особенно в случае сложных и затратных экспериментов). По возможности следует стремиться к тому, чтобы случайная погрешность стала меньше приборной или по крайней мере сравнялась с ней. Нельзя ограничиваться одним наблюдением, оно может содержать промах и по его результату невозможно определить погрешность. Несколько (3…5) повторных наблюдений это тот минимум на основании которого можно оценить ситуацию. Если результаты совпали, то случайные ошибки меньше приборной и на этом количестве наблюдений можно ограничиться. Если в результатах обнаружится разброс, то проводят серию повторных наблюдений, добиваясь уменьшения случайной погрешности.
Таким образом, вопрос о количестве повторных наблюдений решается в ходе эксперимента. На основании анализа полученных результатов, сравнения случайной и приборной погрешностей, учета требований предъявляемых к точности окончательного результата.