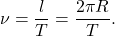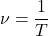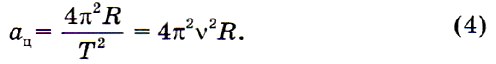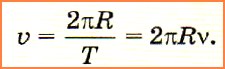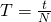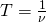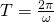Что называется периодом и частотой обращения в каких единицах они измеряются
Движение по окружности, период обращения и частота.
1. Равномерное движение по окружности
Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.
Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.
Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.
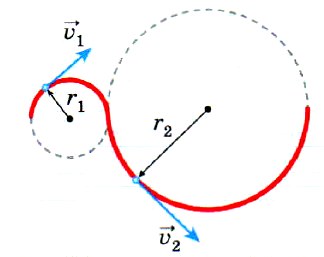
Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.
Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.
2. Период вращения и вращающаяся частота
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.
Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:
Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 
. Итак,
Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:
частота вращения равна количеству полных оборотов за одну секунду.
Частота вращения и период обращения связаны следующим соотношением:
Частоту в СИ измеряют в
3. Вращательное движение
В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.
Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.
Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
ПРОВЕРЬТЕ СЕБЯ
1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.
2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 
Частоту в СИ измеряют в обратных секундах.
3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
Частная школа. 9 класс
Конспекты, контрольные, тесты
Период и частота
Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.
Период и частота
Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.
Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.
С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.
Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?
Очевидно, ν = 1/Т = 1/20 1 /с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
Таким образом, частота обращения является величиной, обратной периоду обращения:
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
или с учётом формулы (1):
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:
Часто мгновенную скорость движения по окружности называют линейной скоростью.
Модуль скорости движения тела по окружности рассчитывается по формуле:
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.
РЕШЕНИЕ ЗАДАЧ
Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.
Ответ: υ = 0,722 м/с.
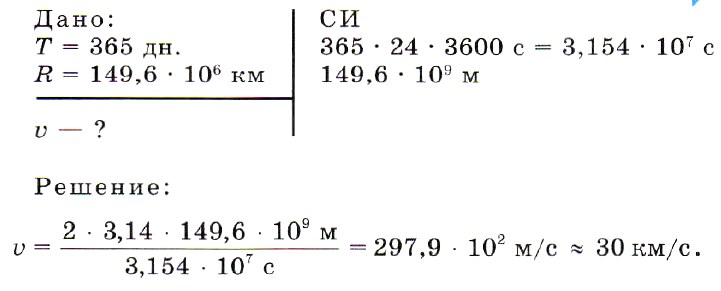
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 10 6 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.
Ответ: υ ≈ 30 км/с.
Вы смотрели Конспект по физике для 9 класса «Период и частота».
План-конспект урока по физике «Период и частота обращения» 9 класс
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Тема: Период и частота вращения.
Цель урока: продолжить изучения криволинейного движения, сформировать понятие о частоте и периоде вращения. Познакомить с формулами для нахождения этих величин и единицами измерения.
Образовательные: продолжить формирование понятие криволинейном движении, величинах его характеризующих, единицах измерения этих величин и формулах для вычисления.
Развивающие: продолжать формирование умений применять теоретические знания для решения практических задач, развивать интерес к предмету и логическое мышление.
Воспитательные: Воспитательные задачи: продолжать развивать кругозор учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.
Тип уроку : изучение и первичное закрепление знаний.
Оборудование: доска, учебник В.В. Белага «Физика, 9», А.Е. Марон «Сборник вопросов и задач, 7-9».
Актуализация опорных знаний.
Изучение нового материала.
Закрепление нового материала.
Подведение итогов. Рефлексия.
ІІ. Актуализация опорных знаний. Проверка Д/з
Какое движение называется криволинейным?
Как направлена мгновенная скорость при движении тела по окружности?
Что такое центростремительное ускорение?
Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?
Как направлена центростремительная сила? По какой формуле она рассчитывается?
Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 2 раза? Увеличении в 5 раз?
Материальная точка движется по окружности с постоянной по модулю скоростью. Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить вдвое?
Решение задач. А.Е. Марон «Сборник вопросов и задач, 7-9» № 1629, 1645, 1648.
III. Изучение нового материала.
Движение тела по окружности характеризуется не только скоростью и ускорением. Когда тело движется по окружности с постоянной по модулю скоростью, то через определённые промежутки времени движение повторяется.
Период – время, в течении которого тело совершает один полный оборот, называют периодом обращения. 
, где t – время всех оборотов, N – число оборотов. 
Период обозначается буквой Т. Формула для нахождения периода, где – время всех оборотов, – количество оборотов. Единицей измерения периода в СИ является секунда.
Частота – число оборотов за единицу времени (секунду). 
, 
(в честь учёного Генриха Герца).
Частота и период обращения связаны между собой. 
, а 
.
Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля, вылетающая из автомата Калашникова, вращается с частотой 3000 об/с.
3. Связь модуля скорости с периодом обращения и частотой.
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности и период или частоту обращения. Один полный оборот тело совершает за время, равное периоду обращения. Путь, пройденный телом равен длине окружности: 
, поэтому 
.
С учётом этого можно найти центростремительное ускорение: 
ІV. Закрепление нового материала.
Что называется периодом и частотой обращения?
В каких единицах они измеряются?
Как эти величины связаны между собой?
Чему равны периоды вращения: часовой, минутной и секундной стрелок часов; Земли вокруг своей оси; Земли вокруг Солнца; Луны вокруг Земли?
Решение задач. А.Е. Марон «Сборник вопросов и задач, 7-9» № 1632, 1631, 1635, 1638, 1641.
V. Д/з. Выучить § 5, решить задачи № 1633, 1634.
Период и частота обращения (окончание)
Число полных оборотов за 1 с называют частотой обращения и обозначают ν.
Частоту измеряют в 
Частота не всегда выражается целым числом. Например, если тело совершает полный оборот за 2 с, то 
период и частота являются взаимно обратными величинами:
Предположим, что тело совершило n полных оборотов за время t. Тогда период обращения
а число оборотов в секунду, то есть частота обращения
Полученные выражения для Т и ν являются взаимно обратными. Доказательство завершено.
Чему равна частота обращения, если период равен 5 с?
Чему равен период обращения, если частота равна 
Во сколько раз частота обращения минутной стрелки часов больше частоты обращения часовой стрелки?
Как сказал.
Есть только два способа прожить жизнь. Первый — будто чудес не существует. Второй — будто кругом одни чудеса.
А.Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Период вращения (обращения)
Период вращения (обращения) — это минимальное время, за которое тело совершает один полный оборот, т.е. поворачивается на угол 2π
Для нахождения периода вращения надо время всех оборотов разделить на количество оборотов:
T — период вращения
N — количество оборотов
t — время, за которое было совершено N оборотов
ν — частота вращения (обращения)
ω — угловая скорость
Законы и формулы
Сейчас 31 гостей и ни одного зарегистрированного пользователя на сайте
Спасибо тем авторам и правообладателям, которые согласны на размещение своих материалов на моем сайте! Вы вносите неоценимый вклад в обучение, воспитание и развитие подрастающего поколения.