Что называется периодической функцией
Периодическая функция
Периодическая функция — это функция, значения которой не изменяются при добавлении к значениям её аргумента некоторого числа T (отличного от нуля).
Функция y=f(x) называется периодической, если существует такое число T≠0, что для любого x из области определения этой функции выполняются равенства:
Число T называют периодом функции y=f(x).
Из определения следует, что значения x-T и x+T также входят в область определения функции y=f(x).
Свойства периодических функций
1) По определению периодической функции для любого x из области определения y=f(x) если T — период функции, то f(x-T)= f(x)=f(x+T).
2) Для любого x из области определения y=f(x) если T1 — период функции, то
Так как T2 также является периодом функции y=f(x), то для аргумента x-T1
Следовательно, число T1+T2 является периодом функции y=f(x).
3) Это свойство непосредственно вытекает из свойства 2, если T взять в качестве слагаемого n раз.
4) Если T — период функции f(x), то для аргумента kx+b
Значит число T/k — период функции f(kx+b).
5) Эти свойства следуют непосредственно из определения.
Например, для суммы f(x) и g(x):
Из свойства 3 следует, что каждая периодическая функция имеет бесконечно много периодов.
Если среди всех периодов функции y=f(x) существует наименьший положительный период, то его называют главным (или основным) периодом функции.
Примеры периодических функций
1) Поскольку для любого x выполняются равенства
то функции y=sin x и y=cos x являются периодическими с периодом T=2π.
2) Так как для любого x из области определения функции y=tg x выполняется равенство
tg (x-π)=tg x =tg (x-π), то y=tg x — периодическая функция с периодом T=π.
Аналогично, y=ctg x — периодическая функция с периодом T=π.
3) Так как для любого действительного числа x и любого рационального числа k выполняется равенство D(x+k)=D(x), то функция Дирихле D(x) — периодическая с периодом T=k, где k∈Q, k≠0.
Поскольку k — любое рациональное число, невозможно его указать наименьшее положительное значение. Следовательно, функция Дирихле не имеет главного периода.
4) Рассмотрим частный случай линейной функции y=b, b — действительное число (b∈R). Эта функция определена на множестве действительных чисел и при любых значениях аргумента принимает единственное значение y=b, то есть для любого действительного числа m (m∈R), y(x)=y(x+m)=b.
Значит y=b — периодическая функция с периодом T=m, где m∈R, m≠0.
Так как m — любое действительное число, оно не имеет наименьшего положительного значения. Поэтому функция y=b не имеет главного периода.
5) Так как для любого действительного x и любого целого k выполняется равенство
Наименьшим положительным целым числом является единица. Следовательно, T=1 — главный период функции y=
Главный период функций y=sin x и y=cos x T=2π.
Главный период функций y=tg x и y=ctg x T=π.
Если T — период функции y=sin x, то sin (x-2π)=sin x = sin (x-2π) для любого x.
То есть любой период функции y=sin x имеет вид 2πn, n∈Z.
Наименьшее положительное значение это выражение принимает при n=1 и оно равно T=2π.
Таким образом, 2π — главный период функции y=sin x.
Аналогично доказываются утверждения о главном периоде функций y=cos x, y=tg x и y=ctg x.
Из 4-го свойства периодических функций непосредственно следует, что для функций y=sin (kx+b) и y=cos (kx+b) (k≠0) наименьший положительный период
а для функций y=tg (kx+b) и y=ctg (kx+b) (k≠0) наименьший положительный период
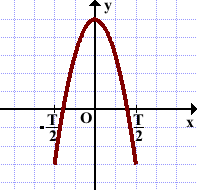
График периодической функции повторяется через промежутки длиной T (на оси Ox).
Дана часть графика
промежутке длиной T.
Чтобы построить график функции, выполняем параллельный перенос этой части графика вдоль оси Ox на ±T, ±2T,… :
Периодические функции
Смотреть что такое «Периодические функции» в других словарях:
ОБОБЩЕННЫЕ ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ — классы функций, являющиеся различными обобщениями почти периодич. функций. Каждый из них обобщает какую то из сторон в определениях Бора почти периодических функций и Бохнера почти периодических функций. В этих определениях встречаются следующие… … Математическая энциклопедия
СТЕПАНОВА ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ — класс Spl измеримых и суммируемых вместе со своей р й степенью в каждом конечном интервале [ х, х+1]функций, к рые могут быть в метрике пространства Степанова (см. ниже) аппроксимированы конечными суммами вида где а n комплексные коэффициенты,… … Математическая энциклопедия
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — класс элементарных функций: синус, косинус, тангенс, котангенс, секанс, косеканс. Обозначаются соответственно: sin x,cos x, tg x,ctg x, sec x,cosec x. Тригонометрические функции действительного аргумента. Пусть А точка окружности с центром в… … Математическая энциклопедия
МАТЬЁ ФУНКЦИИ — периодические решения Матьё уравнения к рые существуют только тогда, когда точка (a, q )на плоскости параметров лежит на границе зон устойчивости. М. ф. четна или нечетна и единственна с точностью до множителя; второе линейно независимое решение… … Математическая энциклопедия
Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия
Что называется периодической функцией
Период функции – положительное число Т, обладающее двумя свойствами:
а) вместе с числом х в область определения данной функции входят также числа х + Т и х – Т;
б) для любого значения х из области определения функции справедливы равенства f(x – T) = f(x) = f(x + T).
Наименьшее из чисел Т, обладающих указанными свойствами, называется основным периодом функции.
Часто основной период функции называют просто ее периодом.
Функция, имеющая период, называется периодической. В школьной программе наиболее часто из периодических функций встречаются основные тригонометрические функции.
Очевидно, что если Т – период функции, то при любом натуральном (т.е. целом положительном) значении k число kT также будет ее периодом. Точнее, если периодическая функция у = f(x) непрерывна на каком-нибудь интервале и не является на нем константой (т.е. постоянной), то для нее существует наименьший период Т; тогда любой период этой функции имеет вид kT, где k – натуральное число.
Для построения графика периодической функции достаточно построить его на любом отрезке длиной в (основной) период, тогда весь график получится сдвигом построенной части вправо и влево на целое число периодов.
Периодическая функция
Примеры реальных чисел
Для функции от действительных чисел или от целых чисел это означает, что весь граф может быть сформирован из копий одной конкретной части, повторяющихся через равные промежутки времени.
Тригонометрические функции синус и косинус являются общими периодическими функциями с периодом 2л (см рисунок справа). Предмет ряда Фурье исследует идею о том, что «произвольная» периодическая функция является суммой тригонометрических функций с совпадающими периодами.
Примеры комплексных чисел
Используя комплексные переменные, мы получаем функцию общего периода:
Сложные функции могут быть периодическими вдоль одной линии или оси в комплексной плоскости, но не на другой. Например, е z <\ displaystyle e ^ 
Двойные периодические функции
Функция, областью определения которой являются комплексные числа, может иметь два несоизмеримых периода, не будучи постоянной. В эллиптических функциях такие функции. («Несоизмеримые» в этом контексте означает, что они не могут быть кратными друг другу.)
Любая функция, состоящая только из периодических функций с тем же периодом, также является периодической (с периодом равным или меньшим), включая:
Антипериодические функции
Блоховско-периодические функции
Факторные пространства как область
Если не существует наименьшего общего знаменателя, например, если один из вышеперечисленных элементов был иррациональным, тогда волна не была бы периодической. [2]
Периодические функции
Понятию периодической функции в разных учебниках даются различные определения, однако независимо от этих различий периодическими являются или не являются одни и те же функции, поэтому говорят, что эти определения равносильны, или эквивалентны, т.е. описывают одно и то же свойство функций, означают одно и то же.
Наиболее просто, по нашему убеждению, дать определение периодической функции в два шага:
2. Функция называется периодической, если она имеет хотя бы один период.
Естественно, функцию называют периодической с периодом Т, если число Т является ее периодом.
Сама форма определения периода подсказывает, что периодов у функции может быть много: в нем подразумевается, что всякое число Т с указанным свойством является периодом функции f, а вы прекрасно знаете, что если Т — период f, то любое его кратное, т.е. число вида nТ, где n — любое целое число, является ее периодом.
Отметим, что не всякая периодическая функция имеет основной, т.е. наименьший положительный период — например, периодом постоянной функции является любое число, отличное от 0, но, пожалуй, самая простая из таких функций, отличных от постоянной, — это «экзотическая» функция Дирихле.
Полезно — особенно для экономии времени при решении задач с кратким ответом — знать, что сумма двух периодических функций с одинаковым периодом является периодической функцией, и более того, для периодичности суммы достаточно, чтобы отношение каких-то двух их периодов Т1 и Т2 являлось рациональным числом (такие числа Т1 и Т2 часто называют соизмеримыми).