Что называется основанием величиной и точностью линейного масштаба

Решение задач по топографическим планам

Масштабы: численный, линейный и поперечный

Масштабом

горизонтальным проложением линии

Применяется три типа масштаба:

численный, линейный и поперечный.

Численным масштабом

Численный масштаб – величина неименованная. Он записывается так: 1:1000, 1:2000, 1: 5000 и т.д., причём в такой записи 1000, 2000 и 5000 называется знаменателем масштаба М.

Численный масштаб говорит о том, что в одной единице длины линии на плане (карте ) содержится точно столько же единиц длины на местности. Так, например, в одной единице длины линии на плане 1:5000 содержится точно 5000 таких же единиц длины на местности, а именно: один сантиметр длины линии на плане 1:5000 соответствует 5000 сантиметрам на местности (т.е. 50 метрам на местности); в одном миллиметре длины линии на плане 1:5000 содержится 5000 миллиметров на местности (т.е. в одном миллиметре длины линии на плане 1:5000 содержится 500 сантиметров или 5 метров на местности) и т.д.

При работе с планом в ряде случаев пользуются линейным масштабом.

Линейный масштаб

Рис.1

Основанием линейного масштаба называется отрезок АВ линейного масштаба (основная доля масштаба), равный обычно 2 см. Он переводится в соответствующую длину на местности и подписывается. Крайнее левое основание масштаба делят на 10 равных частей.

Наименьшее деление основания линейного масштаба равно 1/10 основания масштаба.

Пример: для линейного масштаба (использующегося при работе на топографическом плане масштаба 1:2000), показанного на рисунке 1, основание масштаба АВ равно 2 см (т.е. 40 метрам на местности), а наименьшее деление основания равно 2 мм, что в масштабе 1:2000 соответствует 4 м на местности.

Отрезок cd (рис. 1), взятый с топографического плана масштаба 1:2000, состоит из двух оснований масштаба и двух наименьших делений основания, что, в итоге, соответствует на местности 2х40м+2х2м = 88 м.

Поперечный масштаб

Основание AB нормального поперечного масштаба равно, как и в линейном масштабе, также 2 см. Наименьшее деление основания равно CD =1/10 АВ= 2мм. Наименьшее деление поперечного масштаба равно cd = 1/10 CD =1/100 АВ = 0,2мм (что следует из подобия треугольника BCD и треугольника Bcd).

Таким образом, для численного масштаба 1:2000 основание поперечного масштаба будет соответствовать 40 м, наименьшее деление основания (1/10 основания) равно 4 м, а наименьшее деление масштаба 1/100 АВ равно 0,4 м.

Остановимся на одной из важнейших характеристик понятия «масштаб».

Точностью масштаба называется горизонтальный отрезок на местности, который соответствует величине 0,1 мм на плане данного масштаба. Эта характеристика зависит от разрешающей способности невооруженного человеческого глаза, которая (разрешающая способность) позволяет рассмотреть минимальное расстояние на топографическом плане в 0.1мм. На местности эта величина будет уже равна 0.1 мм х М, где М – знаменатель масштаба.

Рис.2

Поперечный масштаб, в частности, позволяет измерить длину линии на плане (карте) масштаба 1:2000 именно с точностью данного масштаба.

Пример: в 1 мм плана 1:2000 содержится 2000 мм местности, а в 0,1мм, соответственно, 0,1 x М (мм) = 0.1 х 2000 мм = 200 мм = 20 см, т.е. 0,2 м.

Поэтому при измерении (построении) на плане длины линии ее значение следует округлить с точностью масштаба. Пример: при измерении (построении) линии длиной 58,37 м (рис. 3), ее значение в масштабе 1:2000 (с точностью масштаба 0,2 м) округляется до 58,4 м, а в масштабе 1:500 (точность масштаба 0,05 м) – длина линии округляется уже до 58,35 м.

Рис.3

Чтение
топографических планов

Для пользования топографическими планами необходимо изучить условные знаки, принятые для данного масштаба. Условные знаки – графические обозначения, которые показывают местоположение предметов и явлений, а также их количественные и качественные характеристики. Они издаются в виде отдельных таблиц или таблиц на учебных планах. Условные знаки делятся на масштабные (контурные), и внемасштабные.

Масштабными называются условные знаки, которыми местные предметы изображаются в масштабе данного плана, т.е. крупные объекты, например, пашни, луга, леса, моря, озера и т.п.

Внемасштабные условные знаки – знаки, показывающие предметы, которые вследствие своей малости не могут быть изображены в масштабе плана (ширина дорог, колодцы, родники, мосты, опоры ЛЭП, столбы электросети и т.д.). Величина этих знаков не соответствует истинным размерам изображаемых предметов.

Скачать условные знаки для топографических планов:

Задачи, решаемые
по топографическим планам

По топографическому плану можно решить ряд задач, в том числе определить: прямоугольные координаты точки; длину линии; дирекционный угол и румб линии; отметку точки; уклон, крутизну ската и др. Порядок решения этих задач показан на примере учебного плана масштаба 1:2000.

Определение прямоугольных
координат точек

Пример : запись 79,2 означает, что абсцисса линии сетки Х = 79,2 км, т.е. отстоит по оси Х от начала координат на 79200 м. Запись 66,2 означает, что ордината линии сетки Y = 66,2 км, т.е. отстоит по оси У от начала координат на 66200 м.

Для быстрого нахождения какой-нибудь точки на топографическом плане указывают нижний левый угол соответствующего квадрата сетки координат.

Сначала записывают в метрах абсциссу Х (южной) линии квадрата, в котором находится точка А, т.е. Х(южной линии сетки) =79200,0 м. Циркулем и поперечным масштабом определяют расстояние Δх = Y(а)-Y(А) также в метрах с точностью масштаба. Полученную величину Δх=64,8 м прибавляют к абсциссе нижней (южной) линии квадрата Х(южной линии сетки) =79200,0 м и находят абсциссу точки А: Х(А) = 79200,0 + 64,8 = 79264,8 м.

Рис.4

Аналогично определяют ординату точки А: к значению ординаты западной линии сетки квадрата У(западной линии сетки) =66200,0 м прибавляют длину отрезка Δy =y(A)-y(b), равную 141,6 м, и получают Y(А) = 66200,0 + 141,6 = 66341,6 м.

Измерение длин линий

Расстояние между точками А и В измеряется циркулем, значение длины линии АВ находится по поперечному масштабу и записывается с точностью масштаба.

Определение
дирекционного угла

Дирекционным углом α называется горизонтальный угол, отсчитываемый от северного направления осевого меридиана, по ходу часовой стрелки, до направления данной линии.

Дирекционный угол α линии АВ можно измерить с помощью транспортира. На рис. 5 представлены дирекционные углы α₁, α₂, α₃, и α₄ четырех линий М-1, М-2, М-3, М-4.

Рис.5

Рис.6

Связь между прямым и обратным дирекционными углами выглядит так:

Рис.7

Например, если прямой румб равен r _пр = СВ: 350º, то обратный румб равен r _обр= ЮЗ: 350º.

Рис.8

Таблица перехода от дирекционных углов α к румбам r приведена ниже.

Формулы перехода от дирекционных углов к румбам

Определение отметок точек
и крутизны ската линии местности

Высотой Н точки местности называется расстояние по направлению отвесной линии от точки до уровенной поверхности.

Отметкой точки местности называется численное значение высоты точки. Например, Н(А) = 150 м, Н(В) =149 м.

На топографическом плане рельеф изображается надписями отметок отдельных характерных точек, условными знаками (промоина, обрыв и т. п.) и горизонта-лями.

Горизонталями называются замкнутые кривые линии, со-единяющие точки местности с одинаковыми отметками. Горизонтали образуются путём пересечения поверхности местности секущими горизонтальными плоскостями, проведенными через заданное расстояние, которое называется высотой сечения рельефа h.

Заложением называется расстояние d на плане между двумя соседними горизонталями (рис. 9 – 11).

Рис.9

По отметкам двух смежных (соседних) горизонталей можно определить отметку точки, лежащей между ними. Например: отметка первой точки В на нижней (рис. 10) горизонтали H1 = 161 м, отметка второй точки А на верхней (рис. 10) горизонтали H2 = 162 м (т.е. высота сечения рельефа h = 1 м), заложение d = 16,8 м, расстояние от первой горизонтали до точки С равно с = 7,6 м (рис. 10). Тогда (с требуемой точностью до 0,1 м) вычисляем отметку НС точки С по формуле

Рис.11

Чем больше угол наклона, тем скат круче.

Для нашего примера уклон линии местности между горизонталями равен

Источник

Масштаб. Виды масштабов. Точность масштаба

Рис.2.2 Линейный масштаб

По линейному масштабу расстояния измеряют с точностью 0,0 2-0,03 основания или примерно 0,5мм.

Поперечный масштаб – это график или номограмма, построенный с использованием метода пропорционального клина. Его применяют для измерений и построений на картах с повышенной точностью. Обычно его гравируют на металлических линейках или транспортирах, такие линейки называют масштабными. Он может быть построен и на чертежной бумаге. Поперечный масштаб устроен следующим образом. Он имеет вид прямоугольника, разделенного вертикальными, горизонтальными и наклонными линиями. Нижняя горизонтальная линия разделена на отрезки равные 2см, называемые основаниями масштаба, они пронумерованы: ниже линии оснований масштаба на правом краю первого основания подписан ноль, далее 1, 2, 3 и т.д., на левом краю первого основания – 1. Через концы оснований проведены перпендикуляры, которые разделены на 10 частей горизонтальными линиями с расстояниями между ними 2, 2,5 или 3мм. Нижняя и верхняя линии первого основания разделены на 10 частей. Ноль нижнего основания соединен наклонной линией с первым слева от нулевого перпендикуляра делением верхней линии, первый слева нижний со вторым слева верхним и т.д., 9-й нижний с последним (десятым) верхним. Наклонные линии называют трансверсалями. Таким образом, левая часть графика имеет вид горизонтальных и наклонных линий. Фигуры между нулевым перпендикуляром и первой к нему трансверсалью и первым слева перпендикуляром и ближайшей к нему трансверсалью имеют вид пропорционального клина. Расстояния на горизонтальных линиях между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и трансверсалями изменяется от одной сотой на первой горизонтальной линии до одной десятой доли основания на последней – верхнем основании (рис.1б). Так как первое основание разделено на десять частей и перпендикуляр к нему разделен также на десять частей, то минимальное расстояние между вертикальной и наклонной линиями клина на горизонтальной линии составляет одну сотую долю основания, поэтому такой поперечный масштаб называют сотенным. Поперечный масштаб строят в следующем порядке. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба равное 2см. Основания нумеруют: слева от нуля 1, справа – 1, 2,3 и т.д. В конечных точках основания восстанавливают перпендикуляры длиной, равной основанию, или большей длины. Крайние перпендикуляры делят на десять частей, и через полученные точки проводят

Рис. 2.3. Линейный и поперечный масштабы

прямые линии, параллельные линии оснований. Нижнюю и верхнюю линии первого основания делят на десять равных частей. Полученные точки соединяют следующим образом: нулевую точку нижнего основания с первым верхним слева, первую нижнюю – со второй верхней и т.д. девятую нижнюю с десятой верхней, как показано на рис.1б. С помощью поперечного масштаба можно измерить длину отрезка на плане (карте) с точностью половины наименьшего деления клина, т.е. 0,1мм. Для отложения на плане измеренного на местности расстояния (горизонтального проложения), его выражают в долях основания масштаба (целых и дробных) делением на величину основания в заданном масштабе, наносят на график и с него циркулем переносят на план (карту).

Дата добавления: 2015-03-19 ; просмотров: 16760 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Масштабы. Точность масштабов

План и карта. Профиль

ТОПОГРАФИЧЕСКИЕ КАРТЫ И ПЛАНЫ

Картой называется уменьшенное изображение на плоскости значительной части земной поверхности, построенное по определенным математическим законам (проекция Гаусса), учитывающим кривизну Земли. На топографических картах в отличие от географических изображаются значительно меньшие участки местности, но с большей точностью и подробностью, что позволяет решать на них различные инженерно-геодезические задачи, возникающие при проектировании сооружений. Ещё большая подробность и точность изображения земной поверхности достигается на топографических планах.

Планомназывается уменьшенное и подобное изображение горизонтальной проекции участка земной поверхности. При этом кривизна Земли не учитывается (проекция Гаусса-Крюгера).

Профиль – это уменьшенное изображение вертикального разреза местности, выполненное в двух масштабах: по горизонтальной оси или оси расстояний принимается значение одного масштаба, а по вертикальной оси или оси высот выбирается масштаб значительно крупнее для более рельефного изображения перегибов местности (обычно вертикальный масштаб в 10 раз крупнее горизонтального).

Степень уменьшения линий на плане или карте относительно горизонтальных проложений соответствующих линий на местности называется масштабом. Масштаб карты можно определить из отношения

, (15)

В геодезии масштаб выражают простой дробью, в числителе которой всегда единица, а в знаменателе число М, показывающее, во сколько раз длина отрезка на карте меньше длины этого же отрезка на местности. Такой масштаб называется численным.

На картах и планах численный масштаб подписывается ниже чертежа, а под ним даётся его расшифровка. Например, масштаб карты 1: 25000. а ниже можно прочитать «в 1 см плана 250 метров на местности».

В России установлены следующие основные масштабы топографических карт и планов:

Зная численный масштаб карты, можно определить длину линии на местности, измерив её величину на карте. Например, на карте масштаба 1:25000 измерен отрезок l = 3,54 см. Тогда длина соответствующего ему горизонтального отрезка на местности может быть определена из пропорции:

отсюда L= 3,54 x 250 = 885 м.

Аналогично решается и обратная задача, когда измерен горизонтальный отрезок на местности L и его необходимо нанести на карту, то пропорция решается в отношении величины l.

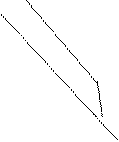
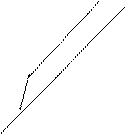
При массовых измерениях и построениях пользоваться формулой (16) не всегда целесообразно, а порой и невозможно (при работе с планом крупного масштаба). Действительно, если взять отрезок длиной, например, 3,54 см, то построить его на плане крупного масштаба проблематично. Кроме того, при массовых измерениях объём таких построений будет значительным. Поэтому при работе с картой используется так называемый линейный масштаб, который практически решает пропорцию (16) графическим способом. Для этого на прямой несколько раз откладывается отрезок длиной 1 или 2 см, называемым основанием масштаба (рис.14).

а в

500 0 500 1000 1500 2000 2500

в 1 см 250 метров масштаба

Рис.14. Схема линейного масштаба

Пользуются линейным масштабом следующим образом. Зафиксировав измерителем отрезок на карте, правую ножку его устанавливают на штрих одного из основных делений так, чтобы другая ножка попала на основание левее 0 (нулевого деления). На рис.14 расстояние между концами ножек циркуля равно 2650 м. В случае несовпадения конца левой ножки с целым делением доли его определяют на глаз.

Линейный масштаб по сравнению с обычной линейкой с миллиметровыми делениями не повышает точности определения длин отрезков, но позволяет отказаться, как отмечалось выше, от решения пропорций и при многочисленных измерениях повысить производительность работ по определению длин отрезков. Точность определения длин линий по линейному масштабу составляет примерно 0,2 деления. Если в основании линейного масштаба принят отрезок в 1 см, то графическая точность(t_л)линейного масштаба будет равна 0,2 мм. Такая точность измерений вполне устраивает исполнителей при работе с картой и не допустима при работе с планом. Чтобы убедиться в этом, следует рассмотреть понятие точности масштабов и производимых измерений.

Точность численного масштаба (t_ч) определяется графической точностью (t_гр) построения любого плана или карты, величина которого принимается равным 0,1 мм, точнее этого отрезки на плане не могут быть изображены. Отсюда следует, что точностью численного масштаба называется горизонтальный отрезок на местности, соответствующий 0,1 мм на карте или плане,

Следовательно, точности указанных выше численных масштабов будут равны:

1: 1 000 000 t = 0,1 мм х 1 000 000 = 100 000 мм = 100 м

1: 100 000 t = 0,1 мм х 1 00 000 = 10 000 мм = 10 м

1: 50 000 t = 0,1 мм х 50 000 = 5 000 мм = 5 м

1: 25 000 t = 0,1 мм х 25 000 = 2500 мм = 2,5 м

1: 10 000 t = 0,1 мм х 10 000 = 1000 мм = 1 м

1: 5000 t = 0,1 мм х 5000 = 500 мм = 0,5 м = 50 см

1: 2000 t = 0,1 мм х 2000 = 200 мм = 0,2 м = 20 см

1: 1000 t = 0,1 мм х 1000 = 100 мм = 0,1 м = 10 см

1: 500 t = 0,1 мм х 500 = 50 мм = 0,05 м = 5 см

Отсюда можно рассчитать точность измерений (построений) длин линий на той или иной карте или плане с использованием линейного масштаба. Как отмечалось выше, графическая точность линейного масштаба равна примерно 0,2 наименьшего деления его. Следовательно, для линейного масштаба с основанием его 1 см графическая точность определения длины отрезка будет равна 0,2 мм, что в 2 раза грубее точности численных масштабов. Если учесть, что в соответствии с теорией вероятности предельная ошибка измерения длин линий может быть в 2-3 раза больше случайной, то точность измерений (построения) длин линий резко падает. Отсюда видно, что глазомерная оценка части делений линейного масштаба снижает точность измерительных работ на планах и картах, особенно при использовании линейных масштабов, в основании которых положен отрезок 2 см и более. Чтобы избежать оценки делений на глаз и повысить точность определения длин линий на карте (плане), применяют поперечный масштаб, называемый в обиходе масштабной линейкой.Он строится на основе линейного масштаба.

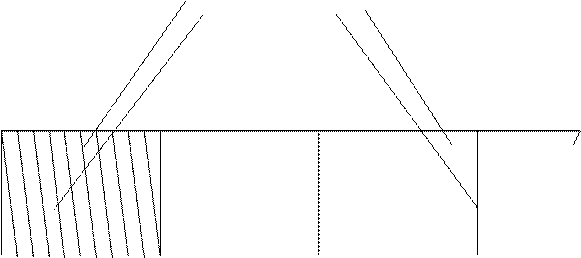
Для этого на прямой откладывают несколько раз отрезок, равный 1 или 2 см, как это было сделано при построении линейного масштаба. Из полученных точек восстанавливают перпендикуляры к этой прямой (рис.15). Крайнее левое основание делят на десять равных частей, а на перпендикулярах откладывают десять таких же делений. Через полученные на перпендикулярах точки проводят параллельные линии. Левое крайнее деление на верхней линии также разбивается на десять равных частей, которые соединяются прямыми с нижними следующим образом: нулевое деление на нижнем основании соединяется с первым на верхнем, первое на нижнем основании со вторым на верхнем. Отрезок “ав” называется наименьшим делением поперечного масштаба или его точностью (t_п), он будет равен 1:100 длины основания масштаба. Такой поперечный масштаб называется нормальнымилисотенным. Точность поперечного масштаба может быть вычислена по формуле

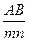
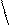
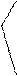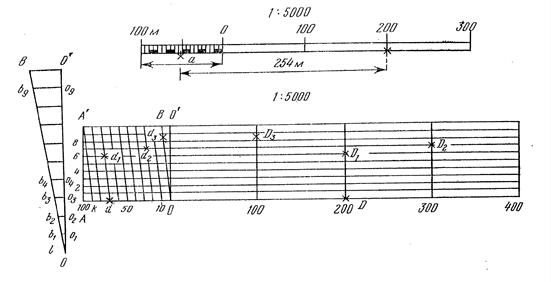
t_п = , (18)

а в

100 70 50 30 10 0 100 200

в 1 см – 100 метров

Рис.15. Схема поперечного масштаба

Если основание масштаба равно 1 см и оно поделено на m=10, а число горизонтальных линий n=10, то точность такого поперечного масштаба будет равно t_п = 1 см/10 х 10 = 0,1 мм, его точность соответствует точности численного масштаба. Если в основании поперечного масштаба будет 2 см и более, то точность определения длины отрезков плана или карты соответственно снизится. Кроме того, все рассуждения о точности поперечного масштаба относятся к масштабным линейкам, изготовленным в заводских условиях с гравировкой линий на металле. Если поперечный масштаб построен графическим путём, то им пользоваться нельзя, так как точность его будет сведена практически к точности линейного масштаба.

Если принять на схеме длину основания 1 см, то поперечный масштаб будет подписан так, как это показано на рис.15. Наименьший отрезок “ав” (на второй горизонтальной линии) будет равен 1 м. Процесс определения длины отрезка, измеренного на карте масштаба 1:10 000, заключается в следующем.

Зафиксировав измерителем отрезок на карте или плане, правую ножку его устанавливают на штрих одного из основных делений так, чтобы другая ножка попала на основание левее нулевого деления (как поступали в случае с линейным масштабом). Если левая ножка циркуля не совпала с целым делением (см. рис.15, вертикальная линия), то циркуль перемещается поступательно вверх до совмещения левой ножки с наклонной линией основания. Длина линии равна сумме отрезков от нулевого деления до правой ножки циркуля плюс число полных малых делений левого основания и плюс число наименьших делений «ав», соответствующее номеру горизонтальной линии, на которой расположены иглы измерителя. На рис.15 расстояние между ножками циркуля в указанном масштабе равно 200 м плюс 60 м и плюс 4 м, то есть 264 м.

Как отмечалось выше, основание поперечного масштаба равно 1 или 2 см. Однако иногда целесообразно брать иной размер основания. Так 1 см рационально брать для численных масштабов 1:1000 и 1:10 000, 2 см для масштабов 1: 500, 1:5000 и 1:50 000, 4 см – 1:25 000, 5 см – 1:2000. Тогда основание масштаба будет кратно 10 м, 100 м и 1000 м.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник