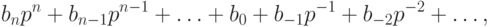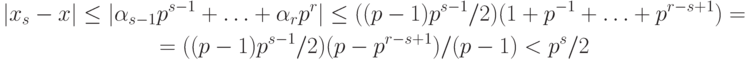Что называется ошибкой округления
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
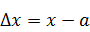
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
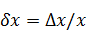
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

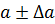
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 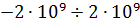
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
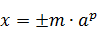
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 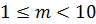
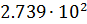
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 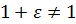
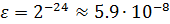
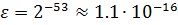
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
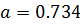
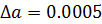
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
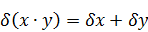
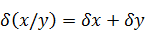
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
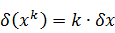
При сложении или вычитании чисел их абсолютные погрешности складываются:
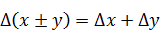
Относительная погрешность суммы положительных слагаемых вычисляется как:
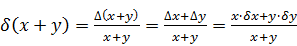
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
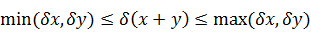
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 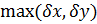
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 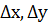
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Ошибка округления
Опубликовано 17.06.2021 · Обновлено 17.06.2021
Что такое ошибка округления?
Ошибка округления или ошибка округления – это математический просчет или ошибка квантования, вызванная изменением числа на целое или на число с меньшим количеством десятичных знаков. По сути, это разница между результатом математического алгоритма, использующего точную арифметику, и того же алгоритма, использующего несколько менее точную округленную версию того же числа или чисел. Значимость ошибки округления зависит от обстоятельств.
Хотя в большинстве случаев ошибка округления достаточно несущественна, чтобы ее игнорировать, она может иметь кумулятивный эффект в современной компьютеризированной финансовой среде, и в этом случае ее, возможно, придется исправить. Ошибка округления может быть особенно проблематичной, когда округленный ввод используется в серии вычислений, что приводит к увеличению ошибки, а иногда и к перевесу вычислений.
Термин «ошибка округления» также иногда используется для обозначения суммы, несущественной для очень большой компании.
Как работает ошибка округления
В финансовых отчетах многих компаний регулярно содержится предупреждение о том, что «цифры могут не совпадать из-за округления». В таких случаях очевидная ошибка вызвана только особенностями финансовой таблицы и не требует исправления.
Пример ошибки округления
Например, рассмотрим ситуацию, когда финансовое учреждение по ошибке округляет процентные ставки по ипотечным кредитам в конкретном месяце, в результате чего с его клиентов взимаются процентные ставки в размере 4% и 5% вместо 3,60% и 4,70% соответственно. В этом случае ошибка округления может затронуть десятки тысяч клиентов, а величина ошибки приведет к тому, что учреждение понесет сотни тысяч долларов расходов на исправление транзакций и исправление ошибки.
Бурный рост больших данных и связанных с ними передовых приложений для анализа данных только увеличил вероятность ошибок округления. Часто ошибка округления возникает случайно; это по своей природе непредсказуемо или иным образом трудно контролировать – отсюда и множество проблем, связанных с «чистыми данными» из больших данных. В других случаях ошибка округления возникает, когда исследователь по незнанию округляет переменную до нескольких десятичных знаков.
Классическая ошибка округления
Классический пример ошибки округления включает историю Эдварда Лоренца. Примерно в 1960 году профессор Массачусетского технологического института Лоренц ввел числа в раннюю компьютерную программу, моделирующую погодные условия. Лоренц изменил одно значение с.506127 на.506. К его удивлению, это крошечное изменение радикально изменило всю схему, созданную его программой, что повлияло на точность моделирования погодных условий за более чем два месяца.
Неожиданный результат привел Лоренца к глубокому пониманию того, как работает природа: небольшие изменения могут иметь большие последствия. Идея стала известна как «эффект бабочки» после того, как Лоренц предположил, что взмах крыльев бабочки может в конечном итоге вызвать торнадо. А эффект бабочки, также известный как «чувствительная зависимость от начальных условий», имеет важное следствие: прогнозирование будущего может быть почти невозможным. Сегодня более элегантная форма эффекта бабочки известна как теория хаоса. Дальнейшие расширения этих эффектов признаны в исследовании фракталов и «случайности» финансовых рынков Бенуа Мандельброта.
ОШИБКА ОКРУГЛЕНИЯ
Смотреть что такое «ОШИБКА ОКРУГЛЕНИЯ» в других словарях:
ошибка округления — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN roundoff error … Справочник технического переводчика
Ошибка округления — (математика) абсолютное значение разности данного числа а и числа а*, получающегося в результате округления (См. Округление) а … Большая советская энциклопедия
ошибка округления — погрешность, возникающая при квантовании в результате округления амплитуды сигнала до ближайшего уровня квантования. Причина возникновения шума квантования … Русский индекс к Англо-русскому словарь по музыкальной терминологии
ошибка отбрасывания — ошибка округления ошибка усечения погрешность отбрасывания — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы ошибка округленияошибка… … Справочник технического переводчика
ошибка отбрасывания (члена формулы) — погрешность метода (формулы) ошибка округления — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы погрешность метода (формулы)ошибка округления EN… … Справочник технического переводчика
ошибка в результате округления — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN round off error … Справочник технического переводчика
Ошибка квантования — Шум квантования ошибки, возникающие при оцифровке аналогового сигнала. В зависимости от типа аналого цифрового преобразования могут возникать из за округления (до определённого разряда) сигнала или усечения (отбрасывания младших разрядов)… … Википедия
НАКОПЛЕНИЕ ПОГРЕШНОСТИ — при численном решении алгебраических уравнений суммарное влияние округлений, сделанных на отдельных шагах вычислительного процесса, на точность полученного решения линейной алгебраич. системы. Наиболее распространенным способом априорной оценки… … Математическая энциклопедия
Погрешность измерения — Сюда перенаправляется запрос «Относительная точность». На эту тему нужна отдельная статья. Сюда перенаправляется запрос «Абсолютная то … Википедия
Гибридный компьютер — У этого термина существуют и другие значения, см. Гибридная вычислительная система. Гибридный компьютер, гибридная вычислительная машина, аналого цифровая система вид гибридной вычислительной системы (ГВС), сочетающий в себе свойства… … Википедия
Ошибка округления
Ошибка округления – разница между вычисленным приближенным значением и точным математическим: округление чисел, правила округления, разница и точность.
Задача обучения
Основные пункты
Термин
Ошибка округления
Ошибка округления – разница между рассчитанным приближенным числом и точным математическим показателем. Численный анализ старается оценить эту погрешность при использовании округлений в уравнениях и алгоритмах. Проблема в том, что если применяются последовательные вычисления, то первоначальная ошибка в округлении способна вырасти до весомой погрешности, которая сильно повлияет на результат.
Подсчеты редко приводят к целым числам. Поэтому мы получаем десятичное с бесконечными цифрами. Чем больше чисел используют, тем точнее подсчеты. Но в некоторых случаях это неприемлемо, особенно при расчетах вручную. Тем более, что человеческое внимание не способно уследить за такими погрешностями. Чтобы упростить процесс, числа округляют до нескольких десятых.
Например, уравнение для нахождения окружности A=πr 2 довольно сложно вычислить, так как число π тянется до бесконечности (абсолютная ошибка округления числа пи), но чаще представляется как 3.14. Технически это снижает точность вычисления, но данное число достаточно близко к реальной оценке.
Однако при следующих расчетах данные будут снова округляться, а значит накапливаются ошибки. Если их много, то не миновать серьезных сдвигов в расчетах.
Вот один из таких примеров:
Округление данных чисел повлияет на ответ. Чем больше округлений, тем больше ошибок.
Компьютеры и ошибки округления
Известно, что при решении задач на компьютере неизбежно возникают ошибки округления. Они крайне малы, но при решении больших задач их появляется очень много. Поэтому в совокупности они могут оказывать значительное влияние на точность получаемых результатов. Тем не менее, в курсах вычислительной математики ошибкам округления уделяется неоправданно мало внимания. Возможно, именно поэтому вокруг ошибок округления возникает немало необоснованных мнений и даже мифов.
Широко распространен миф, согласно которому ошибки округления можно считать случайными величинами. Но, естественно, возникает вопрос, почему они случайные и что это означает? Имеются немало и других необоснованных постулатов. Чтобы они не становились руководством к действию, познакомимся с ошибками округления поближе.
Зафиксируем некоторое целое положительное число р >1 и целые числа 
Такие формы записи чисел называются позиционными системами счисления. Их название связано с тем, что роль, которую играет каждое число 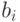

Выбор базисных чисел 

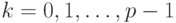
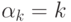
Естественным является желание объединить достоинства обоих способов округления. Покажем, как этого можно добиться путем использования специальных систем счисления.
Среди сокращенных позиционных систем счисления простейшей является троичная система. Как уже отмечалось, в современной вычислительной технике наиболее широко используется двоичная система. С точки зрения округления чисел этот выбор не является лучшим. Но если троичная система счисления так хороша, то почему же нет большого числа построенных на ней компьютеров?
Рядовой пользователь не видит систему счисления, лежащую в основе работы компьютера, поскольку он отгорожен от нее языком программирования. С точки зрения пользователя троичная система хороша только тем, что позволяет без каких-либо дополнительных усилий получать более точные результаты. Безусловно, это очень важно. Однако достижение лучшей точности очень редко становится приоритетным условием для конструкторов компьютеров. Поэтому в первую очередь на выбор системы счисления влияют другие факторы. Это и трудности построения большого числа базисных элементов, имеющих 3 устойчивых состояния, и традиции конструирования элементной базы, и конкуренция в среде производителей компьютеров, и многое другое.
Тем не менее, совсем не очевидно, на каких принципах и с какой целевой функцией будут строиться компьютеры в будущем. И вполне возможно, что троичная система счисления еще окажется востребованной. Тем более что успешный опыт создания компьютера на такой системе имеется. Это машина «Сетунь». Она была разработана в вычислительном центре Московского университета в конце 50-х годов прошлого столетия. Ее главным конструктором является к.т.н. Н.П.Брусенцов, программное обеспечение выполнялось под руководством проф. Е.А.Жоголева.