Что называется ординатой точки
Значение слова «ордината»
[От лат. ordinatus — упорядоченный, назначенный]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В прямоугольной системе координат луч (прямая) Y’Y называется «осью ординат». При построении графиков функций, ось ординат обычно используется как область значений функции.
ОРДИНА’ТА, ы, ж. [латин. ordinata — расположенная на равных расстояниях] (мат.). В системе координат аналитической геометрии — перпендикуляр на плоскости, опущенный из точки на ось абсцисс.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
ордина́та
1. матем. координата точки на оси Y в прямоугольной системе координат ◆ Перемещение точки по абсциссе вызывает сдвиг проекции по ординате.
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: сживать — это что-то нейтральное, положительное или отрицательное?
Прямоугольная система координат. Ось абсцисс и ординат
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Прямоугольная декартова система координат
Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
Прямоугольная система координат в трехмерном пространстве
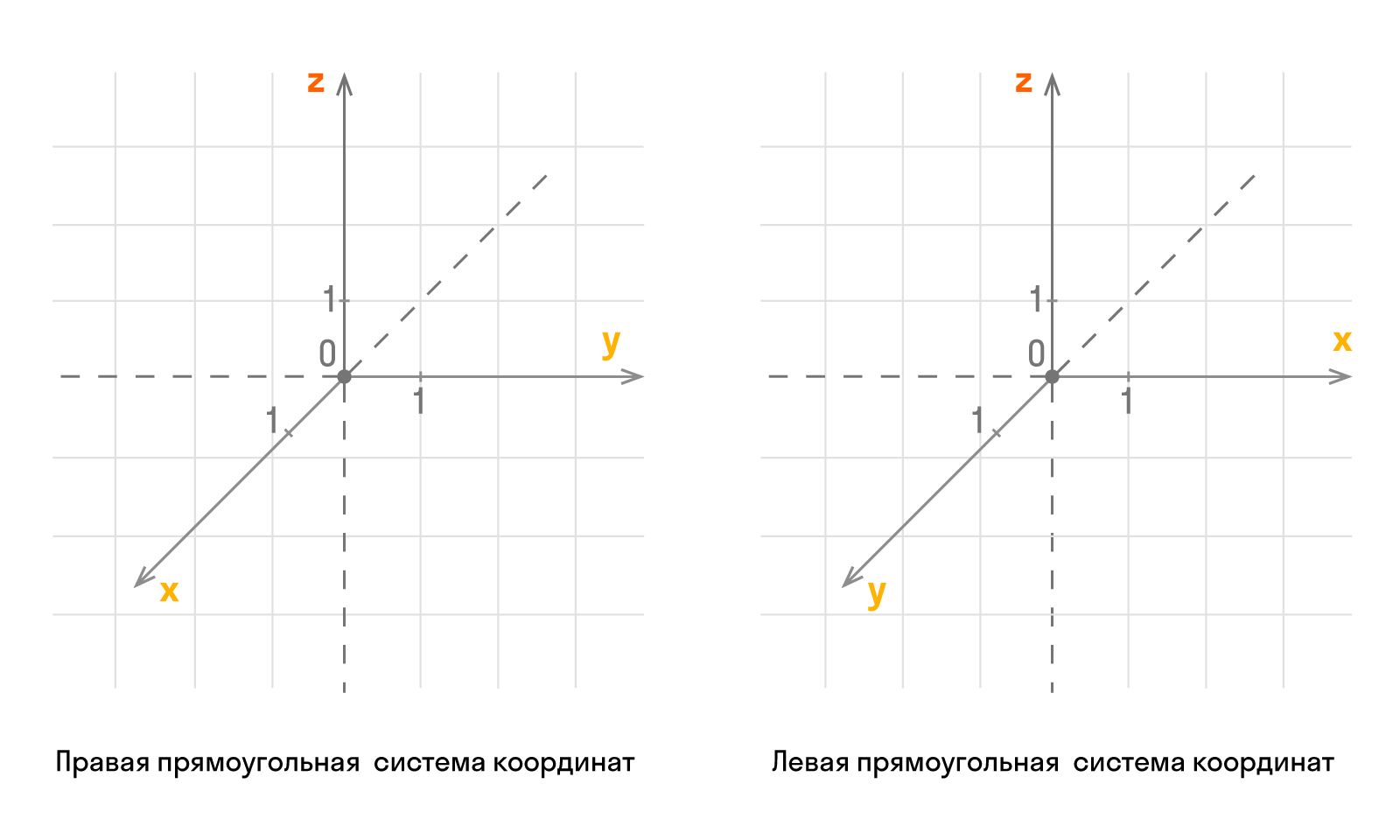
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Координаты точки в трехмерном пространстве
Сформулируем определение точки М в трехмерном пространстве.
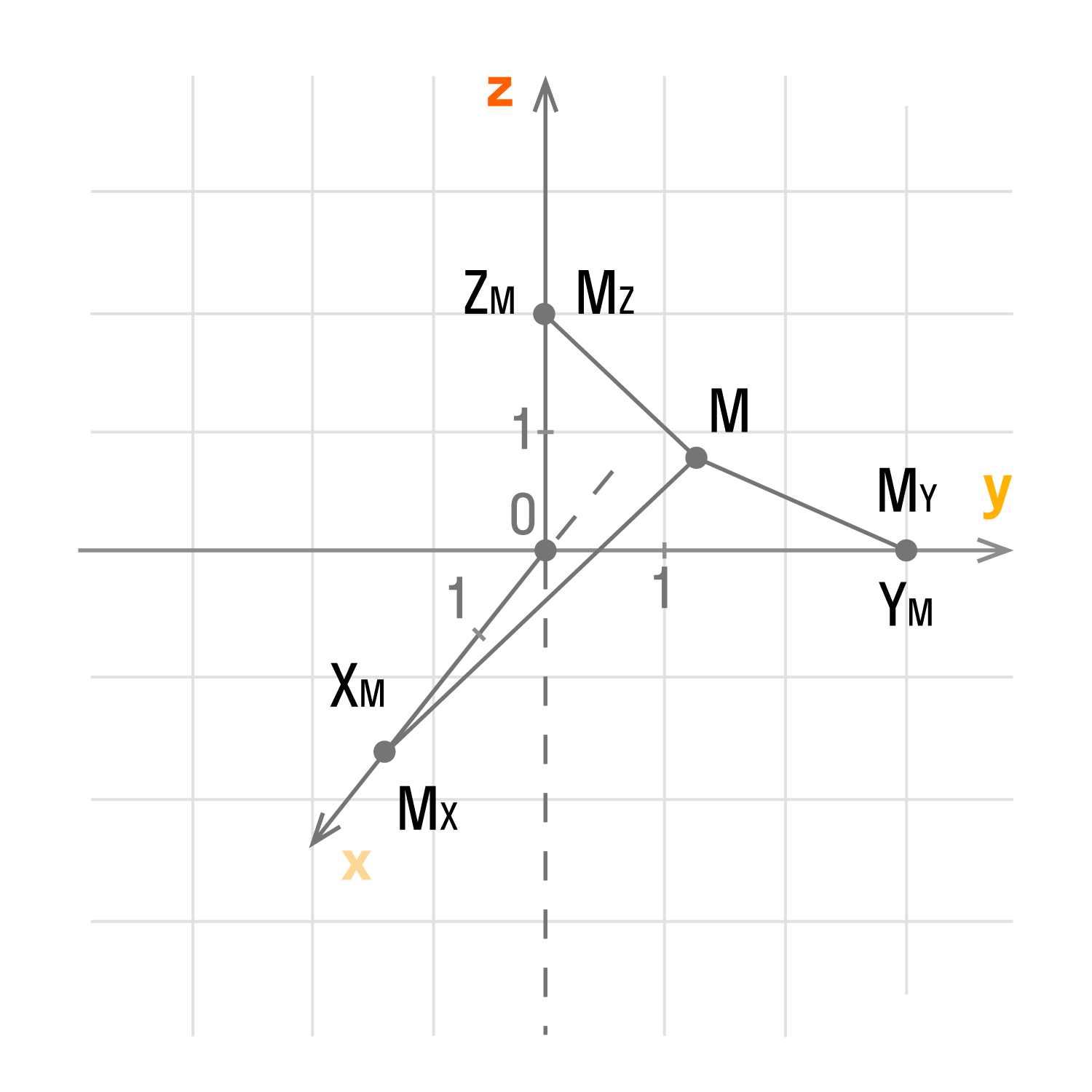
Пусть Mx, My, Mz — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения xM, yM, zM. Как это выглядит на координатных прямых:
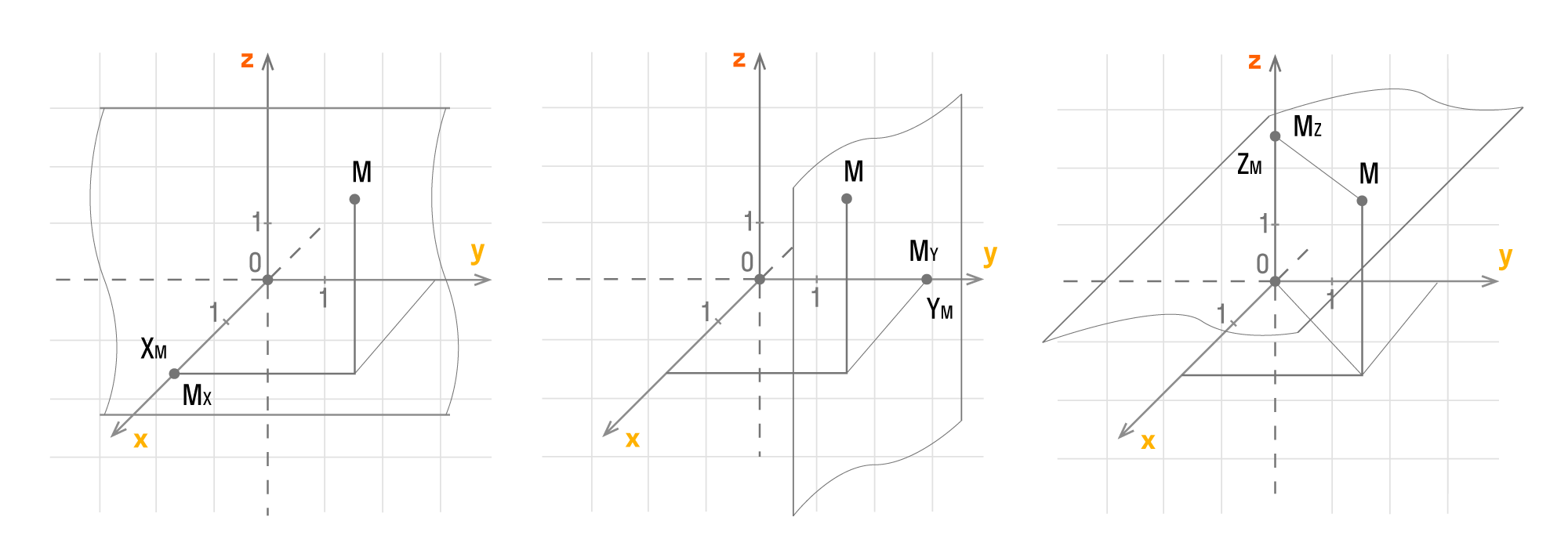
Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в Mx, My, Mz.
У каждой точки трехмерного пространства есть свои данные (xM, yM, zM), которые являются координатами точки М.
xM, yM, zM — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.
ОРДИНАТА
ордината ж. Название одного из двух, трех чисел, определяющих положение точки на плоскости относительно прямоугольной системы координат (в геометрии).
Ордината — Положение точки на плоскости определяется величиной перпендикуляра, опущенного из точки на некоторую данную прямую, называемую осью абсцисс и расстоянием основания этого перпендикуляра до некоторой данной на оси абсцисс точки, называемой началом. Перпендикуляр, опущенный из точки на ось абсцисс, называется О. точки; расстояние же основания О. до начала называется абсциссой точки. О. и абсцисса точки суть ее прямоугольные координаты, которыми определяется ее положение (см. Координаты). При определении положения точки косоугольными координатами, проводятся на плоскости две прямые, называемые осями координат; положение точки определяется величиной ее расстояний от осей, причем эти расстояния считаются по направлениям параллельным осям. Одно из этих расстояний называется абсциссой, а другое О. Прямоугольные координаты представляют собой тот частный случай косоугольных, когда угол между осями есть прямой. Н. Делоне.
◁ ОРДИНАТА 1766, ы, ж.От лат. linea ordinata. Мат. Одна из трех координат, определяющих положение точки в пространстве. Хорды оных кругов будут поперешники (ординаты), а полуденная линея ось оной кривой линеи, что описывает конец т ѣ ни. Кот. Геодет 306. По том д ѣ лается на том цилиндр ѣ параболоид .., у котораго .. самая нижняя ордината в 6 дюймов. Коз. Расс. 173. Ординаты суть прямыя параллельныя лин ѣ и, заключающияся в кривой, кои поперечником перес ѣ каются на дв ѣ равныя части. Ян. III 154.
ОРДИНА́ТА, и, ж.
В геометрії – одне з двох (трьох) чисел, що визначають положення точки на площині відносно прямокутної системи координат.
Ордината
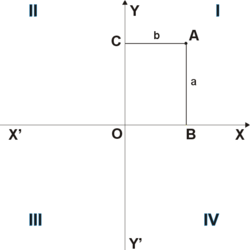
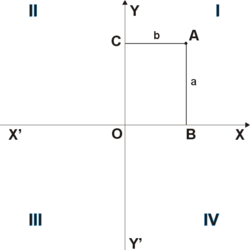
Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат».
См. также
Смотреть что такое «Ордината» в других словарях:
Ордината — Когда данные изображаются в виде графика, ордината соответствует информации, содержащейся на вертикальной оси, или оси «У». При экспериментальных исследованиях на этой оси размещаются значения зависимой переменной. Психология. А Я. Словарь… … Большая психологическая энциклопедия
ОРДИНАТА — (от лат. ordinatus расположенный в порядке) одна из декартовых координат точки, обычно вторая, обозначаемая буквой y … Большой Энциклопедический словарь
ОРДИНАТА — ОРДИНАТА, ординаты, жен. (лат. ordinata расположенная на равных расстояниях) (мат.). В системе координат аналитической геометрии перпендикуляр на плоскости, опущенный из точки на ось абсцисс. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ордината — сущ., кол во синонимов: 1 • координата (4) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ордината — Разность долгот начала и конца профиля, измеренная на данной широте [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN ordinatedeparture … Справочник технического переводчика
ордината — В картографии координата, отсчитываемая по направлению, перпендикулярному осевому меридиану … Словарь по географии
ОРДИНАТА — одно из двух (трёх) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат … Большая политехническая энциклопедия
ордината — (лат. ordinatus упорядоченный, расставленный в известном порядке) ееом. одно из двух (трех) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат. Новый словарь иностранных слов. by EdwART … Словарь иностранных слов русского языка
ордината — ы; ж. [от лат. ordinatus упорядоченный, назначенный] Матем. Величина, определяющая положение некоторой точки на плоскости или в пространстве по оси Y в прямоугольной системе координат (ср. абсцисса, ордината). * * * ордината (от лат. ordinatus … … Энциклопедический словарь
ордината — ordinatė statusas T sritis fizika atitikmenys: angl. ordinate vok. Ordinate, f rus. ордината, f pranc. ordonnée, f … Fizikos terminų žodynas
Ось ординат
В прямоугольной системе координат ось Y’Y называется «осью ординат».
При построении графиков функций, ось ординат обычно используется как область значений функции.
См. также
Смотреть что такое «Ось ординат» в других словарях:
Психометрическая Кривая — график зависимости вероятности обнаружения (или различения) раздражителя от его величины, обычно получаемый в психофизическом эксперименте с помощью метода постоянных раздражителей. Ось ординат представляет собой относительную частоту… … Психологический словарь
Геодезические проекции — отображения поверхности земного эллипсоида (См. Земной эллипсоид) на плоскость, осуществленные по определённым законам. Г. п. применяются для численной обработки геодезических сетей (См. Геодезическая сеть) и для решения различных… … Большая советская энциклопедия
Геохимическая диаграмма — парагенетическая диаграмма, графическое изображение последовательности кристаллизации и последующих преобразований минералов, а также их парагенетических ассоциаций. Г. д. изображают обычно последовательность выделения минералов в какой… … Большая советская энциклопедия
Изменение функции — вариация функции, одна из важнейших характеристик функции действительного переменного. Пусть функция f (x) задана на некотором отрезке [a, b]; её изменением, или полным изменением, на этом отрезке называется верхняя грань сумм … … Большая советская энциклопедия
Аналитическая геометрия — раздел геометрии. Основными понятиями А. г. являются простейшие геометрические образы (точки, прямые, плоскости, кривые и поверхности второго порядка). Основными средствами исследования в А. г. служат метод координат (см. ниже) и методы… … Большая советская энциклопедия