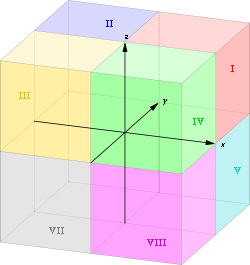
Что называется октантами пространства как они обозначаются
Знаки прямоугольных координат в различных октантах



Таблица 2
ОКТАНТЫ
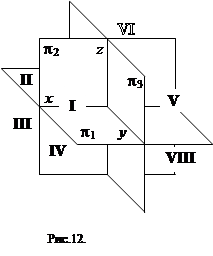
Нумерация октантов в полупространствах приведена на рис. 12. Знаки координат в каждом из октантов указаны в табл. 2.
 |
| № октанта | x | y | z | Положение в пространстве |
| I | + | + | + | ЛПВ |
| II | + | — | + | ЛЗВ |
| III | + | — | — | ЛЗН |
| IV | + | + | — | ЛПН |
| V | — | + | + | Пр.ПВ |
| VI | — | — | + | Пр.ЗВ |
| VII | — | — | — | Пр.ЗН |
| VIII | — | + | — | Пр.ПН |
Обозначения в таблице: Л – левый октант; Пр. – правый октант; П – передний октант;
З – задний октант; В – верхний октант; Н – нижний октант.
ПРОЕЦИРОВАНИЕ ПРЯМОЙ ЛИНИИ
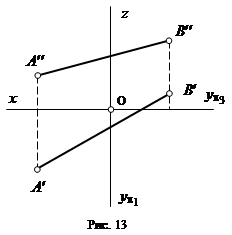
Пусть нам даны на эпюре две точки А и В (рис. 13). Две проекции каждой из этих точек однозначно определяют их положение в пространстве. Если мы соединим одноименные проекции точек, то получим проекции прямой. Точки А и В ограничивают отрезок прямой и определяют положение этой прямой как бесконечной линии.
Таким образом, прямая линия на эпюре может быть задана двумя ее проекциями. По двум проекциям отрезка всегда можно построить его третью проекцию, и притом только одну.
Если прямая не параллельна ни одной из плоскостей проекций, то она пересекает все плоскости проекций и не проецируется ни на одну из них в натуральную величину. Такую прямую называют прямой общего положения. Ни одна из ее проекций не параллельна осям координат. Пример такой прямой изображен на рис. 13.
Октант
Окта́нт ― любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями.
Расчет их ведется в следующем порядке: I, II, III и IV — верхние октанты, которые находятся наверх от x-y-плоскости (z-координата положительна). Они считаются при виде сверху на x-y-плоскость против часовой стрелки. A V, VI, VII, VIII — нижние октанты, которые находятся под x-y-плоскостью. Пятый октант находится под первым, шестой до восьмого тогда опять против часовой стрелки. Знаки координат x, y, z такие:
(«+» здесь значит, что координата больше или равна нулю).
См. ткаже
Квадрант — двухгранный угол, образованный в пространстве пересечением двух плоскостей проекций (например, Π1 и Π2).
Полезное
Смотреть что такое «Октант» в других словарях:
ОКТАНТ — (в морском деле октан) угломерный астрономический инструмент. Шкала октанта составляет 1/8 часть окружности. Октант применялся в мореходной астрономии; практически вышел из употребления … Большой Энциклопедический словарь
октант — I (в морском деле октан), угломерный астрономический инструмент. Шкала октанта составляет 1/8 часть окружности. Октант применялся в мореходной астрономии; практически вышел из употребления. II (лат. Octans), созвездие Южного полушария, в котором … Энциклопедический словарь
ОКТАНТ — (лат. Octans) созвездие Южного полушария, в котором находится Южный полюс мира … Большой Энциклопедический словарь
октант — сущ., кол во синонимов: 1 • созвездие (121) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Октант — Октант. Восьмая часть небесного свода. Источник: НМО ГА 95. Система сертификации на воздушном транспорте. Наставление по метеорологическому обеспечению гражданской авиации (утв. Минтрансом РФ) … Официальная терминология
Октант — 1) (лат. Octans), созвездие Южного полушария, в котором находится Южный полюс мира. 2) (в морском деле октан) угломерный астрономический инструмент. Шкала октанта составляет 1/8 часть окружности. Октант применялся в мореходной астрономии;… … Астрономический словарь
октант — oktantas statusas T sritis Standartizacija ir metrologija apibrėžtis Kampinio atstumo tarp kosminių kūnų matuoklis. atitikmenys: angl. octant rus. октант, m pranc. octant, m ryšiai: susijęs terminas – kvadrantas susijęs terminas – kvadrantas… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
октант — oktantas statusas T sritis Standartizacija ir metrologija apibrėžtis Kampų matuoklis. atitikmenys: angl. octant rus. октант, m pranc. octant, m ryšiai: susijęs terminas – kvadrantas susijęs terminas – kvadrantas susijęs terminas – kvadrantas… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
октант — oktantas statusas T sritis Standartizacija ir metrologija apibrėžtis Viena iš aštuonių sričių, į kurias dalijama erdvė. atitikmenys: angl. octant rus. октант, m pranc. octant, m ryšiai: susijęs terminas – kvadrantas susijęs terminas – kvadrantas… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Точки в четвертях и октантах
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
КАФЕДРА ОБЩЕТЕХНИЧЕСКИХ ДИСЦИПЛИН
точки в четвертях и октантах.
к выполнению семестровой работы
Волгоград
Точки в четвертях и октантах: Методические указания к выполнению семестровой работы по дисциплине «Начертательная геометрия. Инженерная графика» / Сост. ; – Волгоград. гос. техн. ун-та. – Волгоград,
Предлагаемые методические указания с теоретической основой по теме «Точки в четвертях и октантах» и варианты заданий являются руководством к выполнению самостоятельной графической работы для студентов, обучающихся по направлениям: 551700 и 552900 и специальности 100400 сокращенной форме подготовки студентов.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета

В основе правил построения изображений, рассматриваемых в начертательной геометрии и инженерной графике, лежит метод проекций. Изучение его начинают с построения проекций точки, так как при построении изображения любой пространственной формы объекта рассматривается ряд точек, принадлежащих этой форме. Поэтому проецирование точки является базисной основой проецирования сложных геометрических форм.
Проецированием называется процесс построения изображения предмета на плоскости. Получившееся при этом изображение называют проекцией.
1. ЦЕНТРАЛЬНЫЕ, ПАРАЛЛЕЛЬНЫЕ
И ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ
1.1. Центральное проецирование
Для получения центральных проекций при центральном проецировании надо задаться плоскостью проекций (a) и центром проецирования (S) – точкой, не лежащей в этой плоскости (рис. 1). Взяв некоторую точку А и проведя через S и А прямую линию до пересечения ее с плоскостью a, получаем точку Аa. Так же поступаем, например, с точкой В и С. Точки Аa, Вa, Сa являются центральными проекциями точек А, В, С на плоскости a, они получаются в пересечении проецирующих лучей SА, SВ, SС с плоскостью проекций.
Если для некоторой точки D (рис. 1) проецирующий луч окажется параллельным плоскости проекций, то принято считать, что они пересекаются, но в бесконечно удаленной точке.
Не изменяя положения плоскости a и взяв новый центр S1 (рис. 2), получаем новую проекцию точки А – точку Аa1. Если же взять центр S2 на том же проецирующем луче SА, то проекция Аa 2 останется неизменной (Аa º Аa 2).
Следовательно, при заданных плоскости проекций и центре проецирования (рис. 1) можно построить проекцию точки, но имея проекцию (например, Аa), нельзя по ней определить положение самой точки А в пространстве, так как любая точка проецирующим лучом SА проецируется в одну и ту же точку. Для единственного решения, очевидно, необходимы дополнительные условия.
Итак, если при изображении какого-либо предмета все проецирующие прямые проходят через одну точку, то такие проекции называются центральными, а метод проецирования – центральным.
При этом каждая точка пространства будет иметь одну и только одну центральную проекцию.
Центральные проекции применяют для изображения предметов в перспективе. Изображения в центральных проекциях наглядны, но для технического черчения неудобны, так как не соблюдается метрика.
1.2. Параллельное проецирование
Если центр проецирования перенести в бесконечность, то проецирующие лучи станут параллельны, а метод проецирования – параллельным. При этом задается не центр проецирования, а направление проецирования (S¯).
Параллельной проекцией точки называют точку пересечения проецирующего луча, проведенного параллельно заданному направлению, с плоскостью проекций. Каждая точка пространства будет иметь одну и только одну параллельную проекцию (рис. 3).
Если направление проецирования составляет произвольный угол с плоскостью проекций, то параллельное проецирование называют косоугольным.
Параллельное проецирование, как и центральное, не обеспечивает обратимости чертежа.
Параллельные проекции применяют для построения наглядных изображений различных технических устройств и их деталей, например аксонометрических проекций.
1.3. Ортогональное (прямоугольное) проецирование
Если проецирующие лучи перпендикулярны к плоскости проекций, то есть составляют с ней угол 90°, проецирование называется прямоугольным или ортогональным.
Ортогональное проецирование имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях при определенных условиях формы и размеров проецируемой фигуры.
Указанные преимущества обеспечили применение ортогонального проецирования для разработки чертежей во всех отраслях промышленности и в строительстве.
2. ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ И ТРИ
ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ ПРОЕКЦИЙ
2.1. Точка в системе двух плоскостей проекций H и V
 |
В 1799 г. французским ученым Гаспаром Монжем был предложен метод ортогонального проецирования на две взаимно перпендикулярные плоскости проекций. Этим методом пользуются и поныне.
На рис. 4 изображены две взаимно перпендикулярные плоскости проекций. Одна из них, обозначенная буквой Н, расположена горизонтально, другая, обозначенная буквой V – вертикально. Эту плоскость называют фронтальной плоскостью проекций, плоскость Н называют горизонтальной плоскостью проекций.
Линия пересечения плоскостей проекций (Х) называется осью проекций. Ось проекций разделяет каждую из плоскостей Н и V на полуплоскости положительную и отрицательную. Из четырех двугранных углов, образованных плоскостями проекций, считается первым тот, грани которого имеют обозначения Н и V (рис. 4).
На рис. 5 показано построение проекций некоторой точки А в системе Н, V. Проведя из А перпендикуляры к Н и V, получаем проекции точки А: горизонтальную, обозначенную а и фронтальную, обозначенную а¢.
Проецирующие лучи, соответственно перпендикулярные к Н и V, определяют плоскость, перпендикулярную к плоскостям и к оси проекций. Эта плоскость в пересечении с Н и V образует две взаимно перпендикулярные прямые аах и а¢ах, пересекающиеся в точке ах на оси проекций. Следовательно, проекции некоторой точки получаются расположенными на прямых, перпендикулярных к оси проекций и пересекающих эту ось в одной и той же точке.
Если даны проекции а и а¢ некоторой точки А (рис. 6), то, проведя перпендикуляры – через а к плоскости Н и через а¢ к плоскости V – получим в пересечении этих перпендикуляров определенную точку. Итак, две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.
 |
Повернув плоскость Н вокруг оси проекций на угол 90° (как это показано на рис. 7), получим одну плоскость – плоскость чертежа. При этом проекции а¢ и а расположатся на одном перпендикуляре к оси проекций (рис. 8) – на линии связи. В результате указанного совмещения плоскостей Н и V получается чертеж, известный под названием эпюр (эпюр Монжа).
Так как при наличии оси проекций положение точки А относительно плоскостей проекций Н и V установлено, то отрезок аах выражает расстояние точки А от плоскости проекций V, а отрезок а¢ах – расстояние точки А от плоскости проекций Н. Так же можно определить расстояние точки А от оси проекций. Оно выражается гипотенузой треугольника, построенного по катетам аах и а¢ах (рис. 9).
Откладывая на эпюре отрезок а¢а1¢, равный аах, перпендикулярно к а¢ах, получаем гипотенузу а1¢ах, выражающую искомое расстояние.
2.2. Точка в системе трех плоскостей проекций Н, V и W
По двум проекциям также не всегда можно представить пространственный образ предмета. Поэтому при изображении сложных предметов пользуются не двумя, а тремя плоскостями проекций.
Введем в систему Н, V третью вертикальную плоскость проекций W, перпендикулярную оси проекций х и соответственно Н и V (рис. 10).
Ее называют профильной плоскостью проекций. Помимо оси проекций х, появляются еще оси z и y, перпендикулярные к оси х. Буквой О обозначена точка пересечения всех трех осей проекций. Так как ось х ^ W, ось y ^ V, ось
z ^ Н, то в точке О совпадают проекции оси х на плоскость W, оси у на плоскость V и оси z на плоскость Н.
Совместим плоскости проекций Н, V и W в одну плоскость. При этом ось у займет два положения (рис. 10).
 |
Наглядное изображение на рис. 11 и чертеж на рис. 12 содержат горизонтальную, фронтальную и профильную проекции некоторой точки А.
 |
Горизонтальная и фронтальная проекции (а и а¢) расположены на одном перпендикуляре к оси х – на линии связи аа¢, фронтальная и профильная проекции (а¢ и а¢¢) – на одном перпендикуляре к оси z – на линии связи а¢а¢¢.

Расстояние точки А от плоскости Н измеряется на чертеже отрезком а¢ах или отрезком а¢¢ау, расстояние от V – отрезком аах или отрезком а¢¢аz, расстояние от W – отрезком аау или отрезком а¢аz. Поэтому проекцию а¢¢ можно построить и так, как показано на рис. 13, т. е. откладывая на линии связи проекций а¢ и а¢¢ от оси z вправо отрезок, равный аах. Такое построение предпочтительно.
Расстояние от точки А до оси х (рис. 14) измеряется в пространстве отрезком Аах. Но отрезок Аах равен отрезку а¢¢О. Поэтому для определения расстояния от точки А до оси х на чертеже надо взять отрезок lх.
Аналогично, расстояние от точки А до оси у выражается отрезком lу и расстояние от точки А до оси z – отрезком lz.
Итак, расстояния точки от плоскостей проекций и от осей проекций могут быть измерены непосредственно, как определенные отрезки на чертеже. При этом должен быть учтен его масштаб.
3. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ И СИСТЕМА
Точка в пространстве может быть определена не только ее проекциями, но и прямоугольными (декартовыми) координатами.
Координаты точки – числа, выражающие ее расстояния от трех взаимно перпендикулярных плоскостей, называемых плоскостями координат.
Приняв оси и плоскости координат за оси и плоскости проекций, легко заметить, что абсцисса точки (х) – это расстояние ее от плоскости проекций W, ордината (у) – расстояние от плоскости проекций V и аппликата (z) – расстояние от плоскости проекций Н.
Каждая проекция точки определяется двумя координатами (рис. 12): фронтальная – абсциссой х и аппликатой z, горизонтальная – абсциссой х и ординатой у, профильная – ординатой у и аппликатой z. Следовательно, по координатам точки может быть построен и ее эпюр.

Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям.
4. ТОЧКИ В ЧЕТВЕРТЯХ И ОКТАНТАХ ПРОСТРАНСТВА
 |
Как было сказано ранее, плоскости Н и V при пересечении образуют четыре двугранных угла, их называют квадрантами или четвертями пространства. На рис. 16 указан принятый порядок отсчета четвертей. Ось проекций делит каждую из плоскостей Н и V на полуплоскости положительную и отрицательную.
Положение проекций точек на эпюре зависит от того, в какой четверти находится данная точка. Так, если точка В расположена во второй четверти
(рис. 17), то после совмещения плоскостей обе проекции окажутся лежащими над осью х (рис. 18).
Если точка С находится в третьей четверти, то ее горизонтальная проекция после совмещения плоскостей окажется над осью, а фронтальная – под осью х. Наконец, если точка D расположена в четвертой четверти, то обе проекции ее окажутся под осью х. На рис. 17 и 18 показаны точки М и N, лежащие на плоскостях проекций. При таком положении точка совпадает с одной из своих проекций, другая же проекция ее, оказывается лежащей на оси х.
На рис. 19 в системе Н, V изображены точки А и В, расположенные симметрично относительно плоскости Н. На чертеже (рис. 19, справа) горизонтальные проекции таких точек совпадают одна с другой (а º в), фронтальные же проекции находятся на равных расстояниях от оси проекций (а¢ах = в¢вх).
На рис. 20 показана пространственная модель трех взаимно перпендикулярных плоскостей проекций, делящих пространство на восемь трехгранных углов – октантов.
Для получения чертежа, из пространственной модели (рис. 20), совместим плоскости проекций Н и W с плоскостью V. При этом совпадут положительные и отрицательные направления осей х, y и z.
Построение трех проекций точек, расположенных в различных октантах, можно производить в том же порядке, как и для точек I октанта.
На рис. 21 показаны построения проекций точек А, В, С и D, расположенных в октантах II, III, IV и VII соответственно.
Точки могут находиться в биссекторных плоскостях, т. е. в плоскостях, которые делят углы пространства пополам (рис. 22).
Если точка принадлежит биссекторной плоскости, то ее горизонтальная и фронтальная проекции равноудалены от оси х.
На рис. 22 показаны точки А и D принадлежащие первой биссекторной плоскости, делящей первый, третий, пятый и седьмой углы пространства пополам. Точки В и С принадлежащие второй биссекторной плоскости, делящей второй, четвертый, шестой и восьмой угол пространства пополам.
5. УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАНИЯ
Прежде чем приступить к решению задач, необходимо изучить материал по учебной литературе и ответить на вопросы, поставленные к данной работе.
Каждый студент получает отдельный вариант задания, в который входит решение трех задач. Пример решения задач дан в приложении. Вариант назначается преподавателем. Выполненное задание сдается преподавателю в установленные сроки
.
Графическая работа выполняется в карандаше на листе формата А3. Изображения должны быть расположены на поле чертежа рационально. Все промежуточные построения, выполненные тонкими линиями, остаются на листе для проверки преподавателем.
Внутренняя рамка чертежа проводится на расстоянии 20 мм от его левого края и по 5 мм с трех других сторон.
Надписи, а также цифровые и буквенные обозначения должны быть выполнены стандартным шрифтом № 5 по ГОСТ 2.304-81. Толщина и тип линии должны соответствовать ГОСТ 2.303-68.
6. СОДЕРЖАНИЕ И ВАРИАНТЫ ЗАДАНИЯ
Задача № 1. По заданным координатам х, y, z точек А, В, С, D, Е показать их положения на рисунке пространственной модели координатных плоскостей проекций. Назвать углы пространства, в которых располагаются заданные точки. Назвать точки, одинаково удаленные от координатных плоскостей.
Задача № 2. На эпюрах построить три ортогональные проекции точек А, В, С, D, Е.
Задача № 3. Построить ортогональные проекции точек А, В, С, D, Е, F по заданным координатам и указать углы пространства в которых они находятся.
Построить проекции точек А1 и В1, симметричных данным точкам А и В относительно плоскости проекций Н, и проекции точек С1 и D1, симметричных данным точкам С и D относительно плоскости проекций V.
Указать какой биссекторной плоскости принадлежат точки Е и F.