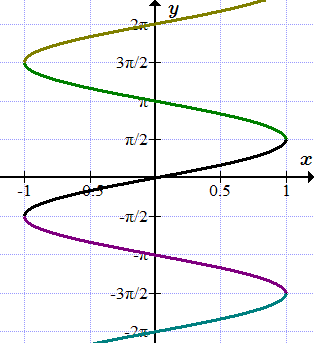Что называется областью функции
Область определения функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
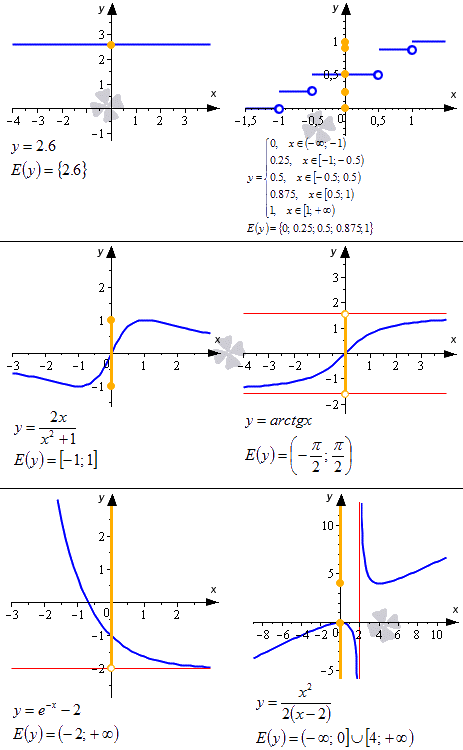
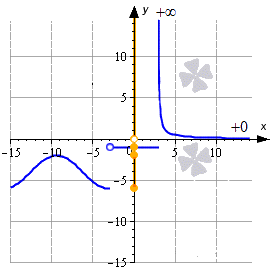
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Рассмотрим основные способы нахождения области значений функции.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Решение
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
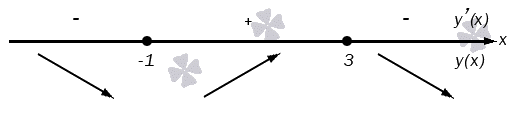
Для определения точек экстремума надо произвести следующие вычисления:
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
Решение
Решение
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Решение
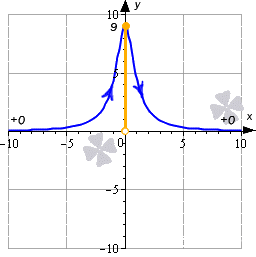
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
Посмотрим, как же ведет себя функция на бесконечности:
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Решение
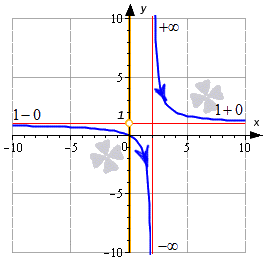
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Решение
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Решение
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Решение
Решение показано на графике:
Решение
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
Теперь найдем соответствующие значения функции:
Посмотрим на поведение функции на бесконечности:
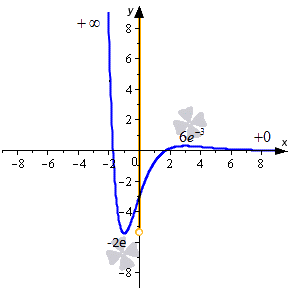
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
Определение числовой функции. Область определения функции. Область значения функции.
Что такое область определения функции? что такое область значения функции? Давайте, в этой статье разберемся в понятиях числовой функции и ее характеристиках и свойствах.
Определение функции.
Функция y=f(x) — это когда каждому допустимому значению переменной x соответствует единственное значение переменной y или другими словами такая зависимость переменной y от переменной x.
х — называется независимой переменной или аргументом.
y – называется зависимой переменной или значением функции.
Множество чисел, где x∈X или D(f) — называется областью определения функции. Это множество всех допустимых значений переменной х.
Область значений функций, когда задаем правило или функцию, которая позволяет по произвольно выбранному значению x∈D(f) вычислить соответствующее значение y.
Переменную х или аргумент мы придумываем сами и подставляем в правило, которое задали или функцию. Далее рассчитываем переменную y или значение функции.
В тех диапазонах в которых существует переменная х называется областью определения функции.
В тех диапазонах в которых существует переменная y называется областью значения функции.
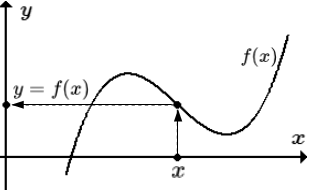
Графиком функции y=f(x), x∈X называется множество точек (x; f(x)) координатной плоскости.
Разберём пример №1:
Найдите область определения и область значения числовой функции y=x 2
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.
А теперь рассмотрим переменную у. В таблице мы видим, что переменная y принимает положительные значение, так как и самое минимальное значение 0. Следовательно, y∈[0; +∞).
Если посмотрим на график, то увидим, что графика ниже нуля нет. Следовательно, область значения функции E(f) = [0; +∞).
Разберём пример №2:
Найдите область определения и область значения числовой функции y=x+1?
Вместо переменной x мы можем брать любые числа и просчитать переменную y.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
По графику также видно, что сколько бы угодно мы не проводили линий через ось х, мы найдем пересечение с графиком.

Рассмотрим переменную у. В таблице мы видим, что переменная y также принимает значения как в положительном, так и в отрицательном направлении. Следовательно, ограничений у переменной y нет, y∈(−∞; +∞). Область значения функции E(f) = (−∞; +∞).
Определение функции
Определение функции
Сложные функции
Действительные функции
В математическом анализе большую роль играют числовые функции.
Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.
Максимум и минимум
Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.
Верхняя и нижняя грани
Монотонные функции
Многозначные функции
Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.
Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.
Сужение и продолжение функции
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Как найти область определения функции?
Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Правила нахождения области определения
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Для нахождения области определения произведения функций необходимо применять правило:
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
Область определения сложной функции
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Тогда получим систему неравенств вида
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Преобразуем систему вида
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Область определения логарифма с переменной в основании
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Область определения показательно-степенной функции
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
Сумма, разность, произведение функций
Расположим функции и их области определения.
Прямая пропорциональность y = k · x
Обратная пропорциональность y = k x
Дробная y = f 1 ( x ) f 2 ( x )
y = log f 2 ( x ) f 1 ( x )
В частности, y = log a f 1 ( x )
В частности, y = log f 2 ( x ) a