Что называется объемной плотностью заряда

СОДЕРЖАНИЕ

Определения

Непрерывные начисления

Ниже приведены определения для непрерывного распределения заряда.

аналогично поверхностная плотность заряда использует элемент площади поверхности d S

а объемная плотность заряда использует элемент объема d V

Общий заряд, разделенный на длину, площадь поверхности или объем, будет средней плотностью заряда:

Бесплатная, обязательная и полная оплата

В диэлектрических материалах общий заряд объекта можно разделить на «свободные» и «связанные» заряды.

Общая плотность заряда

С точки зрения объемной плотности заряда, общая плотность заряда составляет:

Что касается плотности поверхностного заряда:

где нижние индексы «f» и «b» означают «свободный» и «связанный» соответственно.

Связанный заряд

и деление на дифференциальный элемент поверхности dS дает плотность связанного поверхностного заряда:

Ниже приводится более строгий вывод.

Для непрерывного распределения материал можно разделить на бесконечно много бесконечно малых диполей.

используя теорему о расходимости:

который разделяется на потенциал поверхностного заряда ( поверхностный интеграл ) и потенциал, обусловленный объемным зарядом (объемный интеграл):

Плотность свободного заряда

Однородная плотность заряда

Доказательство этого сразу. Начнем с определения заряда любого объема:

Эквивалентные доказательства для линейной плотности заряда и поверхностной плотности заряда следуют тем же аргументам, что и выше.

Дискретные заряды

поэтому дельта-функция гарантирует, что при интегрировании плотности заряда по R общий заряд в R равен q :

Аналогичные уравнения используются для линейной и поверхностной плотностей заряда.

Плотность заряда в специальной теории относительности

Плотность заряда в квантовой механике

При нормировке волновой функции средний заряд в области r ∈ R равен

Приложение

Источник

Сосредоточенные и распределенные заряды

Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.

Сосредоточенный заряд

Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.

Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.

Распределенные заряды

Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.

Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.

Примечание: Плотности отрицательных зарядов записывают со знаком «минус».

Формула линейной плотности заряда

\( \large q \left(\text <Кл>\right) \) – заряд;

\( \large L \left(\text <м>\right) \) – длина, по которой распределен заряд;

\( \large \tau \left(\frac<\text<Кл>><\text<м>> \right) \) – линейная плотность заряда;

Формула поверхностной плотности заряда

Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.

Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).

\( \large S \left(\text<м>^ <2>\right) \) – площадь, по которой распределен заряд;

\( \large \sigma \left(\frac<\text<Кл>><\text<м>^<2>> \right) \) – поверхностная плотность заряда;

Формула объемной плотности заряда

Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.

\( \large V \left(\text<м>^ <3>\right) \) – объем, по которому распределен заряд;

\( \large \rho \left(\frac<\text<Кл>><\text<м>^<3>> \right) \) – объемная плотность заряда;

Примечание:

Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.

Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.

Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.

Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.

Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.

Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.

Источник

Плотность заряда

Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.

Содержание

Плотность заряда в классической физике

Линейная, поверхностная и объемная плотности заряда, обозначаются обычно функциями , и , соответственно, где — это радиус-вектор. Зная эти функции мы можем определить полный заряд:

Плотность заряда в квантовой механике

В квантовой механике плотность заряда, например, электрона в атоме, соотносится с волновой функцией , с помощью следующего соотношения:

причем волновая функция должна иметь нормировку:

Применение

Функция распределения плотности заряда применяется в уравнениях Максвелла.

Литература

См. также

Полезное

Смотреть что такое «Плотность заряда» в других словарях:

плотность заряда — krūvio tankis statusas T sritis fizika atitikmenys: angl. charge density; electric charge density vok. elektrische Ladungsdichte, f; Ladungsdichte, f rus. плотность заряда, f; плотность электрических зарядов, f pranc. densité de charge, f;… … Fizikos terminų žodynas

плотность заряда — krūvio tankis statusas T sritis chemija apibrėžtis Fizikinis dydis, skaitine verte lygus elektros kiekiui vienetiniame tūryje, paviršiuje arba ilgyje. atitikmenys: angl. charge density rus. плотность заряда … Chemijos terminų aiškinamasis žodynas

ПЛОТНОСТЬ ЗАРЯДА — величина, характеризующая распределение электрич. зарядов в пространстве. В зависимости от того, как распределены заряды (по к. л. линии, поверхности или объёму), различают: линейную П. з. т = dQ/dl. где dQ электрич. заряд, находящийся на малом… … Большой энциклопедический политехнический словарь

ПЛОТНОСТЬ ЗАРЯДА — физ. величина, характеризующая распределение электрич. зарядов в пространстве. Различают линейную (выража ется в СИ в Кл/м), поверхностную (Кл/м2) и объёмную П. з. (Кл/м3) … Естествознание. Энциклопедический словарь

объёмная плотность заряда — tūrinio krūvio tankis statusas T sritis fizika atitikmenys: angl. space charge density; spatial charge density; volume charge density vok. Raumladungsdichte, f; räumliche Ladungsdichte, f rus. объёмная плотность заряда, f; плотность объёмного… … Fizikos terminų žodynas

ПОВЕРХНОСТНАЯ ПЛОТНОСТЬ ЗАРЯДА — см.Плотность электрического заряда. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

линейная плотность заряда — ilginis krūvio tankis statusas T sritis fizika atitikmenys: angl. line charge density; linear charge density vok. lineare Ladungsdichte, f rus. линейная плотность заряда, f pranc. densité de charge par unité de longueur, f; densité linéique de… … Fizikos terminų žodynas

линейная плотность заряда — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN linear charge density … Справочник технического переводчика

ЗАРЯДА СОХРАНЕНИЯ ЗАКОН — один из фундаментальных строгих законов природы, состоящий в том, что алгебр. сумма электрич. зарядов любой замкнутой (электрически изолированной) системы остаётся неизменной, какие бы процессы ни происходили внутри этой системы. Установлен в 18… … Физическая энциклопедия

ПЛОТНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА — векторная характеристика тока, равная по модулю электрич. заряду, проходящему за единицу времени через единичную площадку, перпендикулярную направлению упорядоченного движения заряж. ч ц. Если плотность заряда (заряд в единице объёма) r, то П. э … Физическая энциклопедия

Источник

Заряды, плотность заряда. Закон сохранения заряда

Понятие электрического заряда

Понятие электрического заряда будем считать не подлежащим определению. В курсе общей физики дается представление о фактах, на основе которых формируется понятие заряда. Заряд как физическая величина обозначается символом q и измеряется в кулонах (Кл).

Известно, что заряд дискретен, наименьший по абсолютной величине заряд принадлежит элементарной частице – электрону. Классическая электродинамика является макроскопической, то есть рассматривает действие огромных – «практически бесконечных» объемов заряженных частиц. Среда представляется сплошной, а токи и заряды – непрерывно распределенными в объеме.

Распределение заряда q в объеме V характеризуется величиной ρ, которая определяет величину заряда на единицу объема и называется объемной плотностью заряда (17):

Заряд, распределенный в объеме, определяется интегралом через объемную плотность:

.

Рисунок 17 − К определению объемной плотности заряда

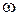
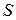
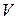
В теории электромагнитного поля применяется также понятие поверхностной плотности заряда. В многих случаях, особенно когда частота изменения поля велика, заряд сосредотачивается в очень тонком слое у поверхности тела . В математических моделях при этом считают, что заряд становится чисто поверхностным (толщина слоя стремится к нулю). Заряд в этом случае определяется как (рисунок 18)

,

где ξ − поверхностная плотность заряда

.

Рисунок 18 − Поверхностная плотность заряда

Наконец, линейный заряд, т.е. распределенный вдоль линии l (например, заряд провода бесконечно малого радиуса, 19) вычисляется как

,

где τ −линейная плотность заряда

.

Рисунок 19 − Линейная плотность заряда

Опытным путем установлен один из основных законов природы: закон сохранения электрического заряда: электрический заряд не уничтожается и не создается из ничего, он может быть лишь перераспределен между телами при их непосредственном контакте.

Ток, плотность тока

Электрический ток (ток проводимости) – упорядоченное движение свободных зарядов под воздействием электрического поля.

Рассмотрим систему, в которой к границе раздела между вакуумом и проводящим веществом подведены два электрода, соединенные с источником электрического тока (рисунок 20). Очевидно, что линии тока внутри вещества распределятся таким образом, что наибольшая часть пройдет по области, представляющей для тока наименьшее сопротивление; гораздо меньшая часть ответвится вглубь тела.

Рисунок 20 − К определению понятия плотности тока

Из рисунка видно, что для исчерпывающей характеристики состояния данной системы недостаточно указать лишь величину тока 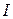, протекающего во внешней цепи. Здесь необходимо располагать сведениями об интенсивности и направлении движения носителей заряда в каждой точке области. С этой целью принято вводить понятие плотности тока проводимости , определяя ее следующим образом (рисунок 21): плотность объемного тока равна заряду, проходящему в единицу времени через единицу площади поверхности, перпендикулярной линиям тока.

Рисунок 21 − Поток тока через поверхность S

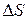
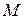
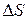
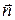
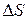
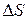
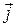
Выделим внутри тела, по которому течет ток, трубку, боковая поверхность которой состоит из линий тока. Заряженные частицы при движении не пересекают стенку трубки. Рассмотрим заряд, переносимый частицами через поперечное перпендикулярное сечение трубки . Скорость -й частицы обозначим вектором , а ее заряд − . Пусть общее количество частиц в объеме равно . Тогда из объема через площадку за время все частицы переносят заряд, равный , где − единичный вектор нормали к поверхности . Тогда , где − вектор объемной плотности тока. Если скорости носителей заряда равны средней , то , где − объемная плотность заряда в объеме . Таким образом, в единицу времени через единичную поверхность , перпендикулярную линиям тока, переносится заряд , определяемый как плотность объемного тока. Единицей измерения является А/м 2 : .

Наряду с объемной плотностью тока, применяются понятия поверхностной и линейной плотности тока.

Электрический ток определяется как поток вектора плотности объемного тока через площадь поверхности :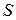

.

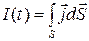
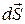
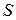
Здесь − вектор, представляющий элементарную площадку поверхности. Таким образом, ток равен заряду, проходящему сквозь за одну секунду. Единицей измерения силы тока является ампер: .

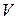
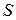
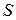
Пусть объем тела ограничен замкнутой поверхностью и в этом объеме находится заряд . Если заряд не остается постоянным, (т.е., уменьшается или увеличивается), то объяснить это следует тем, что поверхность пересекают носители заряда. Иными словами, через поверхность проходит ток, и его величина должна быть связана с зарядом соотношением

.

то есть при уменьшении заряда ток положителен. Так как заряд в объеме определяется по его объемной плотности как , то можно записать:

.

Это выражение называется законом сохранения электрического заряда в интегральной форме, или уравнением непрерывности в интегральной форме.

Источник

Плотность заряда

СОДЕРЖАНИЕ

Определения [ править ]

Непрерывные начисления [ править ]

Ниже приведены определения для непрерывного распределения заряда. [5] [6]

аналогично поверхностная плотность заряда использует элемент площади поверхности d S

а объемная плотность заряда использует элемент объема d V

Общий заряд, разделенный на длину, площадь поверхности или объем, будет средней плотностью заряда:

Бесплатная, связанная и полная оплата [ править ]

В диэлектрических материалах общий заряд объекта можно разделить на «свободные» и «связанные» заряды.

Общая плотность заряда [ править ]

С точки зрения объемной плотности заряда, общая плотность заряда составляет:

Что касается плотности поверхностного заряда:

где нижние индексы «f» и «b» означают «свободный» и «связанный» соответственно.

Связанное обвинение [ править ]

Взяв бесконечно малые :

и деление на дифференциальный элемент поверхности dS дает плотность связанного поверхностного заряда:

Ниже приводится более строгий вывод. [6]

Получение связанной поверхностной и объемной плотности заряда из внутренних дипольных моментов (связанных зарядов)

Электрический потенциал за счет дипольного момента D является: φ = 1 4 π ϵ 0 ( r − r ′ ) ⋅ d | r − r ′ | 3 <\displaystyle \varphi =<\frac <1><4\pi \epsilon _<0>>> <\frac <(\mathbf -\mathbf ‘)\cdot \mathbf > <|\mathbf -\mathbf ‘|^<3>>>> Для непрерывного распределения материал можно разделить на бесконечно много бесконечно малых диполей. φ = 1 4 π ϵ 0 ∭ ( r − r ′ ) ⋅ P | r − r ′ | 3 d 3 r ′ <\displaystyle \varphi =<\frac <1><4\pi \epsilon _<0>>>\iiint <\frac <(\mathbf -\mathbf ‘)\cdot \mathbf > <|\mathbf -\mathbf ‘|^<3>>>d^<3>\mathbf > ∇ ′ ( 1 | r − r ′ | ) ≡ ( e x ∂ ∂ x ′ + e y ∂ ∂ y ′ + e z ∂ ∂ z ′ ) ( 1 | r − r ′ | ) = r − r ′ | r − r ′ | 3 <\displaystyle \nabla '\left(<\frac <1> <|\mathbf -\mathbf ‘|>>\right)\equiv \left(\mathbf _<\frac <\partial ><\partial x'>>+\mathbf _<\frac <\partial ><\partial y'>>+\mathbf _<\frac <\partial ><\partial z'>>\right)\left(<\frac <1> <|\mathbf -\mathbf ‘|>>\right)= <\frac <\mathbf -\mathbf ‘> <|\mathbf -\mathbf ‘|^<3>>>> φ = 1 4 π ϵ 0 ∭ P ⋅ ∇ ′ ( 1 | r − r ′ | ) d 3 r ′ <\displaystyle \varphi =<\frac <1><4\pi \epsilon _<0>>>\iiint \mathbf \cdot \nabla ‘\left(<\frac <1> <|\mathbf -\mathbf ‘|>>\right)d^<3>\mathbf > интеграция по частям φ = 1 4 π ϵ 0 ∭ [ ∇ ′ ⋅ ( P | r − r ′ | ) − 1 r − r ′ ( ∇ ′ ⋅ P ) ] d 3 r ′ <\displaystyle \varphi =<\frac <1><4\pi \epsilon _<0>>>\iiint \left[\nabla ‘\cdot \left( <\frac <\mathbf > <|\mathbf -\mathbf ‘|>>\right)-<\frac <1> <\mathbf -\mathbf ‘>>(\nabla ‘\cdot \mathbf )\right]d^<3>\mathbf > используя теорему о расходимости: который разделяется на потенциал поверхностного заряда ( поверхностный интеграл ) и потенциал, обусловленный объемным зарядом (объемный интеграл): Плотность свободного заряда [ править ] См. Уравнения Максвелла и определяющее соотношение для получения более подробной информации. Однородная плотность заряда [ править ] Доказательство этого сразу. Начнем с определения заряда любого объема: Эквивалентные доказательства для линейной плотности заряда и поверхностной плотности заряда следуют тем же аргументам, что и выше. Дискретные заряды [ править ] ρ q ( r ) = q δ ( r − r 0 ) <\displaystyle \rho _(\mathbf )=q\delta (\mathbf -\mathbf _<0>)> ∫ R d 3 r f ( r ) δ ( r − r 0 ) = f ( r 0 ) <\displaystyle \int _d^<3>\mathbf f(\mathbf )\delta (\mathbf -\mathbf _<0>)=f(\mathbf _<0>)> поэтому дельта-функция гарантирует, что при интегрировании плотности заряда по R общий заряд в R равен q : Q = ∫ R d 3 r ρ q = ∫ R d 3 r q δ ( r − r 0 ) = q ∫ R d 3 r δ ( r − r 0 ) = q <\displaystyle Q=\int _d^<3>\mathbf \,\rho _=\int _d^<3>\mathbf \,q\delta (\mathbf -\mathbf _<0>)=q\int _d^<3>\mathbf \,\delta (\mathbf -\mathbf _<0>)=q> ρ q ( r ) = ∑ i = 1 N q i δ ( r − r i ) <\displaystyle \rho _(\mathbf )=\sum _^\ q_\delta (\mathbf -\mathbf _)\,\!> Q = ∫ R d 3 r ∑ i = 1 N q i δ ( r − r i ) = ∑ i = 1 N q i ∫ R d 3 r δ ( r − r i ) = ∑ i = 1 N q i <\displaystyle Q=\int _d^<3>\mathbf \sum _^\ q_\delta (\mathbf -\mathbf _)=\sum _^\ q_\int _d^<3>\mathbf \delta (\mathbf -\mathbf _)=\sum _^\ q_> Аналогичные уравнения используются для линейной и поверхностной плотностей заряда. Плотность заряда в специальной теории относительности [ править ] Плотность заряда в квантовой механике [ править ] В квантовой механике плотность заряда ρ q связана с волновой функцией ψ ( r ) уравнением ρ q ( r ) = q | ψ ( r ) | 2 <\displaystyle \rho _(\mathbf )=q|\psi (\mathbf )|^<2>> При нормировке волновой функции средний заряд в области r ∈ R равен Q = ∫ R q | ψ ( r ) | 2 d 3 r <\displaystyle Q=\int _q|\psi (\mathbf )|^<2>\,<\rm >^<3>\mathbf > Заявление [ править ] Источник визитки установка дверей шаблоны → Вам также понравится К чему снятся роды подруги во сне 16.05.202216.05.2022 admin 0 двери ирбис для холодильных камер 16.05.202216.05.2022 admin 0 Что значит уважаешь человека уважаешь себя 10.04.202211.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.