Что называется нормальным вектором прямой

Нормальный вектор прямой, координаты нормального вектора прямой.

При изучении уравнений прямой линии на плоскости и в трехмерном пространстве мы опираемся на алгебру векторов. При этом особое значение имеют направляющий вектор прямой и нормальный вектор прямой. В этой статье мы подробно рассмотрим нормальный вектор прямой. Начнем с определения нормального вектора прямой, приведем примеры и графические иллюстрации. Следом перейдем к нахождению координат нормального вектора прямой по известным уравнениям прямой, при этом покажем подробные решения задач.

Навигация по странице.

Нормальный вектор прямой – определение, примеры, иллюстрации.

Для понимания материала Вам необходимо иметь четкое представление о прямой линии, о плоскости, а также знать основные определения, связанные с векторами. Поэтому рекомендуем сначала освежить в памяти материал статей прямая на плоскости, прямая в пространстве, представление о плоскости и векторы – основные определения.

Дадим определение нормального вектора прямой.

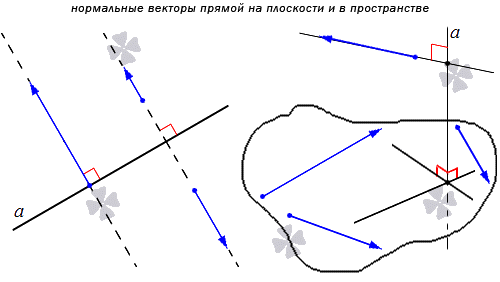
Из определения нормального вектора прямой понятно, что существует бесконечное множество нормальных векторов данной прямой.

Определение нормального вектора прямой и определение направляющего вектора прямой позволяют заключить, что любой нормальный вектор данной прямой перпендикулярен любому направляющему вектору этой прямой.

Приведем пример нормального вектора прямой.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям этой прямой.

Найдем ответ на поставленный вопрос для прямых, заданных на плоскости уравнениями различного вида.

Если прямую линию на плоскости определяет общее уравнение прямой вида , то коэффициенты А и B представляют собой соответствующие координаты нормального вектора этой прямой.

Найдите координаты какого-нибудь нормального вектора прямой .

Одно из чисел A или B в общем уравнении прямой может равняться нулю. Это не должно Вас смущать. Рассмотрим на примере.

Укажите любой нормальный вектор прямой .

Нам дано неполное общее уравнение прямой. Его можно переписать в виде , откуда сразу видны координаты нормального вектора этой прямой: .

Уравнение прямой в отрезках вида или уравнение прямой с угловым коэффициентом легко приводятся к общему уравнению прямой, откуда и находятся координаты нормального вектора этой прямой.

Найдите координаты нормального вектора прямой .

От уравнения прямой в отрезках очень легко перейти к общему уравнению прямой: . Следовательно, нормальный вектор этой прямой имеет координаты .

Также можно получить координаты нормального вектора прямой, если привести каноническое уравнение прямой или параметрические уравнения прямой к общему уравнению. Для этого производят следующие преобразования:

Как способ предпочесть – решать Вам.

Покажем решения примеров.

Найдите какой-нибудь нормальный вектор прямой .

Второй способ решения.

Перейдем от канонического уравнения прямой к общему уравнению: . Теперь стали видны координаты нормального вектора этой прямой .

или

Укажите координаты какого-либо нормального вектора прямой, заданной параметрическими уравнениями .

Перейдем к общему уравнению этой прямой. Для этого выполним следующие действия:

Теперь видны координаты нормального вектора прямой: .

Если прямая задана уравнениями двух пересекающихся плоскостей и , то ее нормальным вектором является как нормальный вектор плоскости , так и нормальный вектор плоскости , то есть, векторы и .

Источник

Нормальный вектор прямой, координаты нормального вектора прямой

Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.

Нормальный вектор прямой – определение, примеры, иллюстрации

Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.

Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.

Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.

Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.

Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой

При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.

Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.

Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:

Для решения можно выбирать любой удобный способ.

Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем

Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:

Источник