Что называется невозможным событием
НЕВОЗМОЖНОЕ СОБЫТИЕ
— событие, к-рое в рамках данных условий не осуществляется ни при каких обстоятельствах. Если 
— вероятностное пространство, то Н. с.- это событие 
, не наступающее ни с одним из элементарных исходов 
(пустое множество). Н. с. является дополнением к достоверному событию
. в рассматриваемой вероятностной модели и поэтому Н. с. приписывают вероятность нуль: 
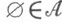
Смотреть что такое «НЕВОЗМОЖНОЕ СОБЫТИЕ» в других словарях:
невозможное событие — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
невозможное событие — negalimasis įvykis statusas T sritis fizika atitikmenys: angl. null event vok. unmögliches Ereignis, n rus. невозможное событие, n pranc. événement nul, m … Fizikos terminų žodynas
Невозможное событие — Невозможным событием в теории вероятностей называется событие, которое не может произойти в результате эксперимента. То есть событие, не содержащее ни одного элементарного исхода (что соответствует «пустому множеству» Ø в пространстве… … Википедия
событие с нулевой вероятностью — невозможное событие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы невозможное событие EN null event … Справочник технического переводчика
событие с нулевой вероятностью — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
ДОСТОВЕРНОЕ СОБЫТИЕ — событие, которое априори должно обязательно произойти. Точнее, если W=
Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Nullereignis — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
Невозможное событие
Невозмо́жным собы́тием в теории вероятностей называется событие, которое не может произойти в результате эксперимента. То есть событие, не содержащее ни одного элементарного исхода (что соответствует «пустому множеству» Ø в пространстве элементарных исходов). [1]
Легко доказать, что вероятность невозможного события равна нулю.
Важно заметить, что обратное неверно, то есть из нулевого значения вероятности не следует, того, что данное событие является невозможным.
Пример 1: Событие, состоящее в том, что нормальнораспределенная случайная величина примет некоторое конкретное значение. Для любой непрерывной случайной величины верно утверждение: вероятность того, что случайная величина примет определенное, наперед заданное значение равна нулю (
).
Пример 2: Эксперимент состоит в том, что монета подбрасывается бесконечное число раз. Событие «Монета бесконечное число раз упадет цифрой вверх» имеет нулевую вероятность, но оно может произойти.
При применении вероятностных методов так же вводят определение практически невозможного события.
Практически невозможным событием называют событие, вероятность которого не выше определённой наперёд заданной величины.
Событие, противоположное невозможному, называется достоверным событием.
Примечания
Полезное
Смотреть что такое «Невозможное событие» в других словарях:
невозможное событие — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
невозможное событие — negalimasis įvykis statusas T sritis fizika atitikmenys: angl. null event vok. unmögliches Ereignis, n rus. невозможное событие, n pranc. événement nul, m … Fizikos terminų žodynas
событие с нулевой вероятностью — невозможное событие — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы невозможное событие EN null event … Справочник технического переводчика
событие с нулевой вероятностью — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
ДОСТОВЕРНОЕ СОБЫТИЕ — событие, которое априори должно обязательно произойти. Точнее, если W=
Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Nullereignis — negalimasis įvykis statusas T sritis automatika atitikmenys: angl. impossible event; null event vok. Nullereignis, n; unmögliches Ereignis, n rus. невозможное событие, n; событие с нулевой вероятностью, n pranc. événement impossible, m; événement … Automatikos terminų žodynas
Что называется невозможным событием
Событиями являются и результаты различных опытов, наблюдений и измерений.
1) из ящика с разноцветными шарами наугад вытаскивают белый шар;
2) на один из приобретенных лотерейных билетов выпал выигрыш;
3) при бросании игральной кости выпала цифра 6.
События делятся на достоверные, случайные и невозможные.
Достоверным называется событие, если оно обязательно произойдет в данном испытании.
Случайным называется событие, если оно может произойти, но может и не произойти в данном испытании.
Невозможным называется событие, если оно не может произойти в данном испытании.
За единицу принимают вероятность достоверного события, а вероятность невозможного события считают равной нулю. Тогда вероятность Р любого события А удовлетворяет неравенству:
Несовместными называются события, если появление одного из них
Пример. Опыт состоит в подбрасывании монеты, событие А – выпадение орла, событие В – выпадение решки. Эти события несовместны, равновозможны и единственно возможны.
Равновозможными называются события, если ни одно из них не является более возможным, чем другое.
Единственно возможными называются события, если в результате опыта хотя бы одно из них обязательно наступит. Говорят, что единственно возможные события образуют полную группу событий .
Рассмотрим классический метод определения вероятности некоторого случайного события. Пусть в результате некоторого опыта могут наступить события А1, А2, А3, …, Аn (элементарные исходы опыта), которые являются:
1)единственно возможными, т.е. в результате опыта хотя бы одно из них обязательно наступит;
2)несовместными, т.е. появление одного из них исключает появление всех остальных;
3)равновозможными, т.е. не существует никаких причин, в связи с которыми одно из событий появлялось бы чаще, чем остальные.
Пусть при появлении некоторых из этих событий наступает событие А. Обозначим число таких событий k (k≤n). А при появлении остальных (n-k) событий событие А не наступает. Говорят, что k событий (элементарных исходов), при которых появляется событие А, благоприятствуют событию А, а остальные (n-k) событий не благоприятствуют ему.
Вероятностью события А называется отношение числа k элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n, если они равновозможны, несовместны и единственно возможны.
1.2.1. Виды событий
Одно из базовых понятий тервера уже озвучено выше – это событие. События бывают достоверными, невозможными и случайными.
1) Достоверным называют событие, которое в результате испытания (осуществления определенных действий, определённого комплекса условий) обязательно произойдёт. Например, в условиях земного тяготения подброшенная монета непременно упадёт вниз.
3) И, наконец, событие называется случайным, если в результате испытания оно может, как произойти, так и не произойти, при этом должен иметь место принципиальный критерий случайности: случайное событие – есть следствие случайных факторов, воздействие которых предугадать невозможно или крайне затруднительно. Пример: в результате броска монеты выпадет «орёл». В рассмотренном случае случайные факторы – это форма и физические характеристики монеты, сила и направление броска, сопротивление воздуха и т.д.
Подчёркнутый критерий случайности очень важен – так, карточный шулер может очень ловко имитировать случайность и давать выигрывать клиенту, но ни о каких случайных факторах, влияющих на итоговый результат, речи не идёт.
Любой результат испытания называется исходом, который, собственно и представляет собой появление определённого события. В частности, при подбрасывании монеты возможно 2 исхода (случайных события): выпадет орёл, выпадет решка. Естественно, подразумевается, что данное испытание проводится в таких условиях, что монета не может встать на ребро или, скажем, зависнуть в невесомости.
События (любые) обозначают большими латинскими буквами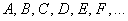 
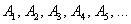
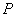
либо теми же буквами с подстрочными индексами, например: 
. При этом стараются избегать буквы 
, которая зарезервирована под другие нужды.
Запишем следующие случайные события:
– в результате броска монеты выпадет «орёл»;
– в результате броска игральной кости (кубика) выпадет 5 очков;
– из карточной колоды будет извлечена карта трефовой масти.
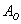
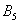
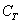
Да, события прямо так и записывают в практических задачах, при этом в уместных случаях удобно использовать «говорящие» подстрочные индексы (хотя можно обойтись и без них).
И следует в третий раз подчеркнуть, что случайные события обязательно удовлетворяют вышеприведённому критерию случайности. В этом смысле особо показателен 3-й пример: если из колоды изначально удалить все карты трефовой масти, то событие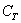 
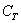
становится невозможным. Наоборот, если испытателю известно, что, например, дама треф лежит снизу, то он при желании может сделать событие 
достоверным =) Таким образом, в данном примере предполагается, что карты хорошо перемешаны и их «рубашки» неразличимы, т.е. колода не является краплёной.
Важной характеристикой случайных событий является их равновозможность. Два или бОльшее количество событий называют равновозможными, если ни одно из них не является более возможным, чем другое. Например:
– выпадение орла или решки при броске монеты;
– выпадение 1, 2, 3, 4, 5 или 6 очков при броске игрального кубика;
– появление трефы, пики, бубны или червы при случайном извлечении карты из полной колоды.
При этом предполагается, что монета и кубик однородны и имеют геометрически правильную форму, а колода хорошо перемешана и «идеальна» с точки зрения неразличимости рубашек карт.
Могут ли быть те же события НЕ равновозможными? Легко. Так, если у монеты или кубика смещён центр тяжести, то гораздо чаще будут выпадать вполне определённые грани. Если кто-то ловко спрятал в рукаве туза треф, то становится менее возможным, что оппоненту будет сдана трефа, и, главное, менее возможно, что будет сдан туз.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Что называется невозможным событием
Вероятность — это числовая характеристика возможности наступления какого-либо события. Вероятностью события А называется отношение числа m случаев, благоприятствующих его наступлению, к числу n всех возможных случаев. Обозначение:
Если событие наступить не может, оно называется невозможным. Вероятность невозможного события равна 0. Если событие непременно наступает, оно называется достоверным. Вероятность достоверного события равна 1. Вероятность события — число из отрезка [0; 1].
Произведением событий А и В называется событие С = AB, состоящее в том, что в результате испытания произошло и событие А, и событие В, то есть оба события произошли.
Суммой событий А и В называется событие С = А + В, состоящее в наступлении, по крайней мере, одного из них, то есть в наступлении события А, или события В, или обоих этих событий вместе.
Два события называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае события называются несовместными.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают 1.