Что называется натуральными числами
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Натуральные числа
Натура́льные чи́сла — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые числа — натуральными числами не являются.
Множество всех натуральных чисел принято обозначать знаком 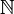
Существует бесконечное множество натуральных чисел — для любого натурального числа найдется другое натуральное число, большее его.
Содержание
Определение
Аксиомы Пеано
Теоретико-множественное определение
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Классы эквивалентности этих множеств относительно биекций также обозначают 0, 1, 2, ….
Замечание
В русской литературе обычно ноль исключен из числа натуральных чисел 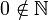
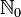
Если в определение натуральных чисел включен ноль, то множество натуральных чисел записывается как 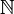
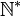
Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Теоретико-множественные определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:
где 
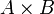
Основные свойства
Алгебраическая структура
Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел 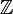
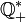
Числа. Натуральные числа.
Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Всякое натуральное число легко записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000. – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Обозначение натуральных чисел: Множество натуральных чисел обозначают символом N.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Сравнение натуральных чисел.
Таблица разрядов и классов чисел.
1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч
1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов
4-й класс миллиарды
1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы.
Основные свойства натуральных чисел.
Действия над натуральными числами.
1. Сложение натуральных чисел результат: сумма натуральных чисел.
Формулы для сложения:
В основном, сложение натуральных чисел выполняется « столбиком ».
2. Вычитание натуральных чисел – операция, обратная сложению: разница натуральных чисел.
Формулы для вычитания:
Вычитание натуральных чисел удобно производить « столбиком ».
3. Умножение натуральных чисел : произведение натуральных чисел.
Формулы для умножения:
(а + b) ∙ с= а ∙ с + b ∙ с
(а – b) ∙ с = а ∙ с – b ∙ с
4. Деление натуральных чисел – операция, обратная операции умножения.
Формулы для деления:
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо.
Когда в выражении есть скобки – сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.











