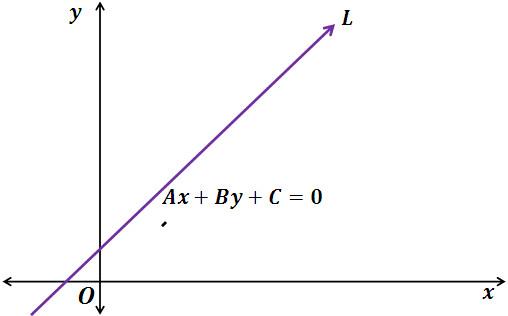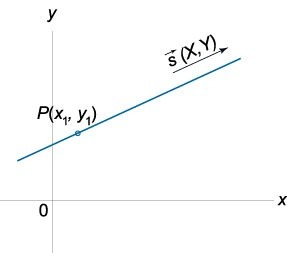Что называется направляющим вектором прямой
Направляющий вектор прямой: определение и примеры
Важным геометрическим объектом, который изучают в плоском пространстве, является прямая. В трехмерном же пространстве, помимо прямой, появляется еще плоскость. Оба объекта удобно задавать с помощью направляющих векторов. Что это такое, как применяют эти вектора для определения уравнений прямой и плоскости? Эти и другие вопросы освещаются в статье.
Прямая и способы ее задавания
Каждый школьник хорошо представляет, о каком геометрическом объекте идет речь. С точки зрения математики, прямая представляет собой набор точек, которые в случае их попарного произвольного соединения между собой приводят к получению совокупности параллельных векторов. Это определение прямой используют для написания уравнения для нее как в двумерном, так и в трехмерном пространстве.

Для описания рассматриваемого одномерного объекта пользуются разными видами уравнений, которые перечислены в списке ниже:
Каждый из названных видов имеет некоторые преимущества по отношению к другим. Например, уравнением в отрезках удобно пользоваться при изучении поведения прямой относительно осей координат, уравнение общего вида удобно при нахождении направления, перпендикулярного заданной прямой, а также при вычислении угла ее пересечения с осью x (для плоского случая).

Поскольку тема данной статьи связана с направляющим вектором прямой, то далее будем рассматривать только уравнение, где этот вектор является принципиальным и содержится явно, то есть векторное выражение.
Задание прямой через вектор
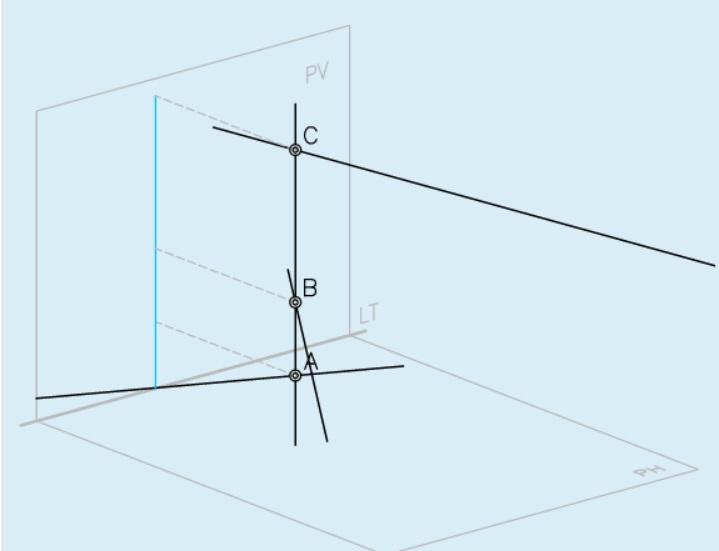
Предположим, что у нас имеется некоторый вектор v¯ с известными координатами (a; b; c). Поскольку координат три, то вектор задан в пространстве. Как изобразить его в прямоугольной системе координат? Делается это очень просто: на каждой из трех осей откладывается отрезок, длина которого равна соответствующей координате вектора. Точка пересечения трех перпендикуляров, восстановленных к плоскостям xy, yz и xz, будет концом вектора. Началом же его является точка (0; 0; 0).
Тем не менее приведенное положение вектора не является единственным. Аналогичным образом можно нарисовать v¯, располагая его начало в произвольной точке пространства. Эти рассуждения говорят о том, что задать конкретную прямую с помощью вектора нельзя. Он задает семейство из бесконечного числа параллельных прямых.
Теперь зафиксируем некоторую точку P(x0; y0; z0) пространства. И зададим условие: через P должна проходить прямая. В этом случае вектор v¯ тоже должен содержать эту точку. Последний факт означает, что можно задать одну единственную прямую, используя P и v¯. Она запишется в виде следующего уравнения:
В координатной форме уравнение запишется так:
(x; y; z) = (x0; y0; z0) + λ × (a; b; c)
И в явном (параметрическом) виде можно записать:
Если в приведенных выражениях исключить третью координату, то мы получим векторные уравнения прямой на плоскости.
Как правило, это задачи на определение параллельности и перпендикулярности прямых. Также определяющий направление прямой вектор используется при вычислении дистанции между прямыми и точкой и прямой, для описания поведения прямой относительно плоскости.
Две прямые будут параллельными, если таковыми являются их направляющие вектора. Соответственно, перпендикулярность прямых доказывается с помощью перпендикулярности их векторов. В этих типах задач достаточно рассчитать скалярное произведение рассматриваемых векторов, чтобы получить ответ.
В случае задач на вычисление расстояний между прямыми и точками направляющий вектор входит явно в соответствующую формулу. Запишем ее:
Отметим, что рассчитывать расстояние между прямыми имеет смысл только тогда, когда они являются параллельными или скрещивающимися. Если же они пересекаются, то d равно нулю.
Приведенная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой, только в этом случае P1 должна принадлежать плоскости.
Решим несколько задач, чтобы нагляднее показать, как пользоваться рассматриваемым вектором.
Задача на составление векторного уравнения
Известно, что прямая описывается следующим равенством:
Следует написать соответствующее выражение в векторной форме.
Это типичное уравнение прямой, известное каждому школьнику, записано в общем виде. Покажем, как его переписать в векторной форме.
Выражение можно представить в виде:
Видно, что если его раскрыть, то получится исходное равенство. Теперь разделим его правую часть на два вектора так, чтобы только один из них содержал иксы, имеем:
Остается вынести x за скобки, обозначить его греческим символом и поменять вектора правой части местами:
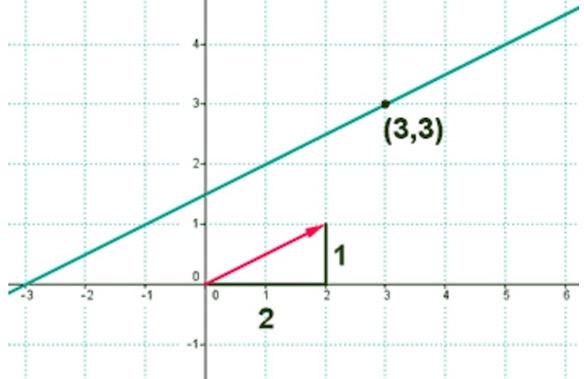
Мы получили векторную форму записи исходного выражения. Координаты направляющего вектора прямой равны (1; 3).
Задача на определение взаимного расположения прямых
В пространстве заданы две прямые:
(x; y; z) = (3; 2; 2) + γ × (1; 2; 0)
Они являются параллельными, скрещивающимися или пересекающимися?
Ненулевые вектора (-1; 3; 1) и (1; 2; 0) будут направляющими для этих прямых. Выразим в параметрической форме эти уравнения и подставим координаты первого во второе. Получаем:
Подставляем найденный параметр λ в два уравнения выше, получаем:
Параметр γ не может одновременно принимать два разных значения. Это означает, что прямые не имеют ни одной общей точки, то есть являются скрещивающимися. Параллельными они не являются, так как ненулевые векторы не параллельны друг другу (для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго).
Математическое описание плоскости
Для задания плоскости в пространстве приведем уравнение общего вида:
A × x + B × y + C × z + D = 0
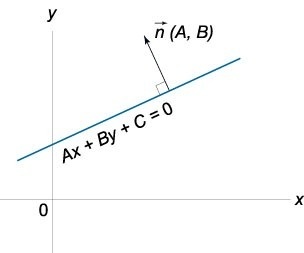
Здесь латинские большие буквы представляют собой конкретные числа. Первые три из них определяют координаты нормального вектора плоскости. Если его обозначить n¯, тогда:
Этот вектор является перпендикулярным плоскости, поэтому его называют направляющим. Его знание, а также известные координаты какой-либо точки, принадлежащей плоскости, однозначно задают последнюю.
Если точка P(x1; y1; z1) плоскости принадлежит, тогда свободный член D рассчитывается следующим образом:
Решим пару задач с использованием общего уравнения для плоскости.
Задача на нахождение нормального вектора плоскости
Плоскость задана в следующем виде:
Как найти направляющий вектор для нее?
Из приведенной выше теории следует, что координаты нормального вектора n¯ являются коэффициентами, стоящими перед переменными. В связи с этим для нахождения n¯ следует записать уравнение в общем виде. Имеем:
Тогда нормальный вектор плоскости равен:
Задача на составление уравнения плоскости
Даны координаты трех точек:
Как будет выглядеть уравнение плоскости, содержащей все эти точки.
Через три точки, которые одной прямой не принадлежат, можно провести только одну плоскость. Чтобы найти ее уравнение, сначала вычислим направляющий вектор плоскости n¯. Для этого поступим следующим образом: найдем произвольные два вектора, принадлежащие плоскости, и вычислим их векторное произведение. Оно даст вектор, который этой плоскости будет перпендикулярен, то есть n¯. Имеем:
Возьмем точку M1 для составления выражения плоскости. Получаем:
Мы получили выражение общего типа для плоскости в пространстве, определив сначала направляющий вектор для нее.
Свойство векторного произведения следует запомнить при решении задач с плоскостями, поскольку оно позволяет простым способом определять координаты нормального вектора.
Направляющий вектор прямой
Вы будете перенаправлены на Автор24
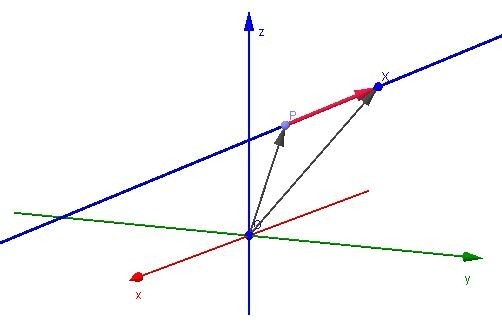
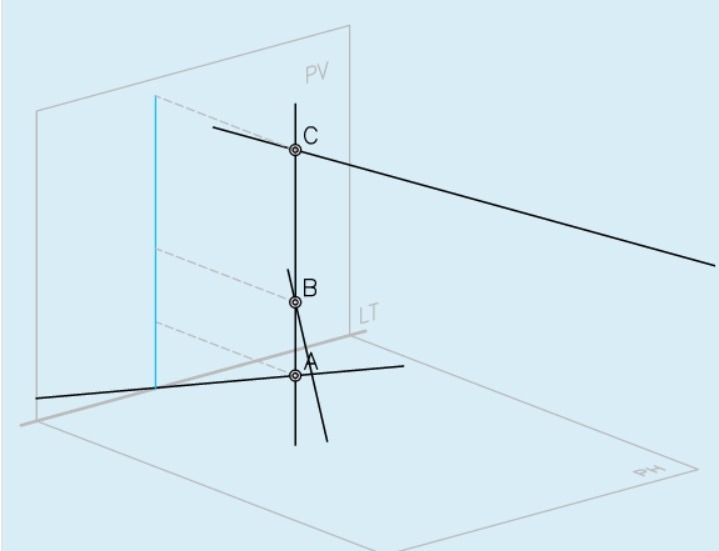
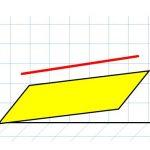
Направляющим вектором прямой называется вектор, параллельный прямой, которую он определяет или совпадающий с ней.
$\overline
Рисунок 1. Направляющий вектор прямой L
$\overline \left(3\right)$
Данное равенство носит название векторного уравнения прямой.
Возможны следующие варианты задания уравнения прямой на плоскости:
Для каждого из этих вариантов подходит свой способ нахождения направляющего вектора.
Направляющий вектор из канонического уравнения прямой и через две точки
Готовые работы на аналогичную тему
Каноническое уравнение прямой выглядит так:
Из канонического уравнения выразить координаты направляющего вектора проще всего: достаточно выписать знаменатели из уравнения следующим образом:
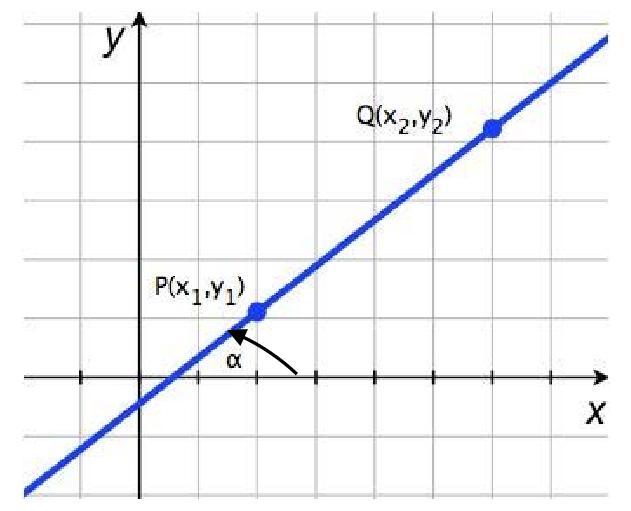
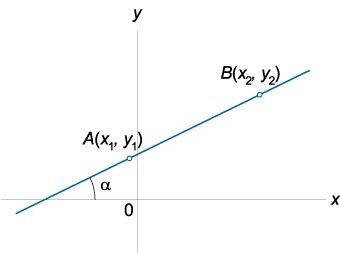
Уравнение прямой, проходящей через 2 точки, имеет вид, очень похожий на каноническое уравнение:
Направляющий вектор из параметрических уравнений
Координаты направляющего вектора из общего уравнения
Общее уравнение имеет следующий вид:
$Ax + By + C = 0\left(6\right)$
Для того чтобы получить координаты направляющего вектора, нужно от общего уравнения прямой перейти к каноническому.
Сделаем это в общей форме.
Координаты направляющего вектора из уравнения с угловым коэффициентом
Уравнение с угловым коэффициентом имеет вид:
Для того чтобы получить из него координаты направляющего вектора, необходимо сначала привести его к общему виду, для этого переносим всё в левую часть:
Затем нужно воспользоваться алгоритмом для общего уравнения.
Уравнение с угловым коэффициентом, приведённое к каноническому, выглядит так:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 25 02 2021
Определение направляющего вектора прямой и как его найти
Направляющий вектор прямой
В геометрии можно встретить множество задач на изучение прямой в пространстве и ее свойств. В трехмерном пространстве рассматривают не только прямую, но и плоскость. Данные объекты достаточно просто задать, используя направляющие векторы.
Направляющим вектором прямой является любой ненулевой вектор, находящийся на рассматриваемой прямой или на прямой, параллельной ей.
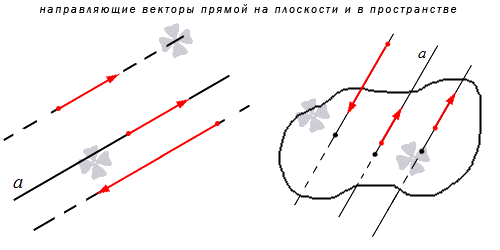
Согласно определению, можно сделать вывод о существовании бесконечного множества направляющих векторов прямой, которая задана. Кроме того, какой-либо направляющий вектор прямой расположен либо на рассматриваемой прямой, либо на прямой, которая ей параллельна. Таким образом, все направляющие векторы заданной прямой коллинеарны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Исходя из термина направляющего вектора прямой, следует, что множества направляющих векторов параллельных прямых совпадают. По-другому, данное утверждение можно сформулировать так: в том случае, когда прямые а и а1 параллельны, вектор \(\vec\) является направляющим вектором прямой а, при этом вектор \(\vec\) также является направляющим вектором прямой а1.
Кроме того, из определений направляющего вектора прямой и нормального вектора прямой следует, что каждый нормальный вектор прямой а является перпендикуляром каждому направляющему вектору прямой а.
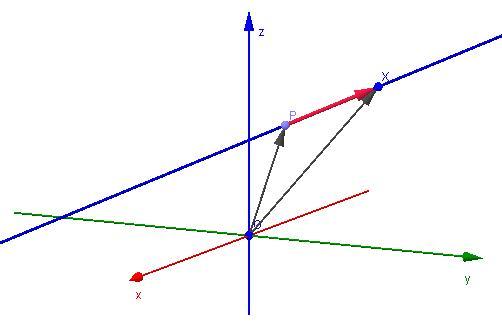
На примере можно рассмотреть направляющий вектор прямой. Предположим, что в трехмерном пространстве имеется прямоугольная система координат Охуz. Координатные векторы \( \vec, \ \vec
Три перпендикуляра, которые восстановлены к плоскостям xy, yz и xz, будут пересекаться в точке, являющейся концом вектора. Начало вектора совпадает с точкой (0; 0; 0). Однако рассматриваемое положение вектора не единственное. Таким же образом можно задать вектор \(\vec
Отсюда следует вывод о невозможности задания конкретной прямой с помощью вектора. С его помощью можно определить комплекс из бесконечного числа параллельных прямых.
где Q является любой точкой, которая принадлежит рассматриваемой прямой.
Параметрический вид уравнения:
Можно преобразовать приведенные формулы путем исключения третьей координаты. В этом случае получим векторные уравнения прямой на плоскости.
Когда нужно знать направляющий вектор
Данные знания пригодятся при решении задач на определение параллельности и перпендикулярности прямых. Кроме того, направляющий вектор используют для расчета расстояния между прямыми, а также точкой и прямой, описания поведения прямой относительно плоскости.
Одна прямая будет параллельна второй прямой в том случае, когда их направляющие вектора параллельны. Аналогично, перпендикулярность прямых доказывают через перпендикулярность их векторов. Подобные задачи предполагают необходимость определения скалярного произведения рассматриваемых векторов для получения ответа.
Когда требуется вычислить расстояние между прямыми и точками, целесообразно использовать формулу с направляющим вектором:
Следует заметить, что рассчитывать расстояние целесообразно только между параллельными или скрещивающимися прямыми. В том случае, когда прямые пересекаются, d обладает нулевым значением. Записанная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой. Но при этом P1 расположена в рассматриваемой плоскости.
Задача на составление векторного уравнения
Представим, что имеется следующее уравнение прямой:
Необходимо записать векторное уравнение данной прямой.
Допустимо переписать выражение в виде:
При раскрытии данного уравнения будет получено выражение из условия.
Далее можно разделить правую часть уравнения на вектора таким образом, чтобы лишь один из них включал неизвестные:
Затем следует вынести х за скобки, обозначить его \(\lambda\) и поменять вектора правой части местами:
Таким образом, получена векторная форма уравнения прямой из условия. Координаты ее направляющего вектора равны (1; 3).
Задача на определение взаимного расположения прямых
Представим, что в пространстве задана пара прямых:
\((x; y; z) = (3; 2; 2) + \lambda * (1; 2; 0)\)
Необходимо определить, какие эти прямые: параллельные, скрещивающиеся или пересекающиеся. При этом ненулевые вектора (-1; 3; 1) и (1; 2; 0) являются направляющими для заданных прямых. Можно выразить в параметрической форме рассматриваемые уравнения и подставить координаты первого во второе:
При подстановке определенного параметра \(\lambda \) в два уравнения выше, получится:
Для параметра \(\gamma\) не предусмотрено наличие сразу двух значений. Таким образом, прямые не обладают ни одной общей точкой, то есть являются скрещивающимися. Параллельность данных прямых исключается, так как ненулевые векторы не параллельны друг другу, то есть для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго.
Математическое описание плоскости
Задать плоскость в пространстве можно путем приведения уравнения общего вида:
\(A * x + B * y + C * z + D = 0\)
Его знание, а также известные координаты любой точки, находящейся на плоскости, однозначно задают последнюю. Если точка P (x1; y1; z1) плоскости принадлежит, то свободный член D рассчитывается следующим образом:
Уравнение прямой по направляющему вектору
Согласно определению, коэффициенты должны соответствовать следующим условиям:
1 * A + (-1) * B = 0, то есть А = В
Ax + Ay + C = 0, или x + y + C / A = 0
Если х = 1, у = 2 получаем:
Общее уравнение прямой в декартовой системе координат имеет вид:
В том случае, когда прямая задана общим уравнением:
В таком случае вектор:
Его координаты соответствуют коэффициентам A, B. Данный вектор представляет собой вектор нормали к данной прямой.
Уравнение прямой по точке и направляющему вектору представляет собой каноническое уравнение прямой и имеет вид:
где вектор \(\mathbf\left(
Координаты направляющего вектора из общего уравнения
При рассмотрении данной темы стоит привязать рассматриваемую прямую и ее направляющие векторы к прямоугольной системе координат. Алгоритм действий:
Прямая линия в прямоугольной системе координат Oxy определяется некоторым уравнением прямой на плоскости. При этом направляющие вектора прямой в системе координат Oxy соответствуют координатам направляющих векторов.
Определить координаты направляющего вектора прямой при известном уравнении рассматриваемой прямой можно в том случае, когда прямая линия задана каноническим уравнением или параметрическими уравнениями.
Каноническое уравнение прямой на плоскости можно записать в виде:
Один из направляющих векторов этой прямой можно записать так:
Отсюда следует вывод о том, что числа в знаменателях канонического уравнения прямой соответствуют координатам направляющего вектора рассматриваемой прямой.
Уравнение определено в прямоугольной системе координат Oxy:
Необходимо рассчитать координаты любого направляющего вектора данной прямой.
Подобным образом можно определить прямую с направляющим вектором \(\vec(a_
Таким образом, коэффициенты при параметре в параметрических уравнениях прямой представляют собой соответствующие координаты направляющего вектора прямой.
Прямая на плоскости задана с помощью параметрических уравнений:
В первую очередь следует преобразовать уравнение прямой:
Коэффициенты с параметром \(\lambda\) соответствуют координатам направляющего вектора прямой:
Далее можно рассмотреть принцип поиска координат направляющего вектора прямой, заданной общим уравнением прямой вида: \(Ax + By + C = 0.\)
Ели А=0 в выражении Ах + Ву + С = 0, то уравнение будет записано в виде:
Данное уравнение определяет прямую, которая параллельна оси абсцисс. Таким образом, направляющим вектором прямой \(Ву + С = 0\) является координатный вектор \(\vec(1; 0).\)
Если В=0, то запись общего уравнения прямой будет следующая:
Данная прямая параллельна оси ординат. В связи с этим, ее направляющим вектором будет координатный вектор \(\vec
Имеется прямая х-2=0, которая расположена на плоскости. Необходимо указать координаты любого направляющего вектора данной прямой.
С помощью уравнения х-2=0 в прямоугольной системе координат Oxy можно задать прямую, которая будет параллельна оси Oy. Таким образом, роль ее направляющего вектора играет координатный вектор \(\vec
В том случае, когда общее уравнение прямой имеет вид \(Ах + Ву + С = 0\) с коэффициентами А и В, не равными нулю, координаты направляющего вектора находят одним из следующих методов:
Наиболее простым способом является приведение общего уравнения прямой к каноническому виду. В результате можно найти координаты направляющего вектора данной прямой.
Требуется определить координаты направляющего вектора прямой, исходя из ее общего уравнения на плоскости, которое имеет вид:
В первую очередь необходимо привести общее уравнение прямой к каноническому виду. В данном случае в левой части выражения остается лишь слагаемое 3х, а остальные компоненты следует перенести в правую часть, меняя знак на противоположный:
Преобразованное равенство имеет вид:
Полученное уравнение позволяет сделать вывод о том, что координаты направляющего вектора равны (2;-3).
Координаты направляющего вектора из уравнения с угловым коэффициентом
Уравнение с угловым коэффициентом записывают в таком виде:
Определить координаты направляющего вектора прямой, описанной данным уравнением, можно с помощью приведения рассматриваемого уравнения к общему виду. В процессе требуется перенести компоненты в левую часть:
Далее можно прибегнуть к алгоритму, характерному для общего уравнения. Уравнение с угловым коэффициентом, преобразованное в каноническое, запишем следующим образом:
Таким образом, координаты направляющего вектора для данного случая равны:
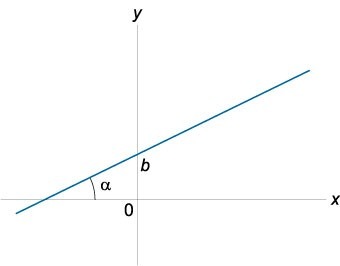
Уравнение прямой с угловым коэффициентом:
где \(k = \tan\alpha\) представляет собой угловой коэффициент прямой, число b определяется, как координата точки пересечения прямой с осью Oy.
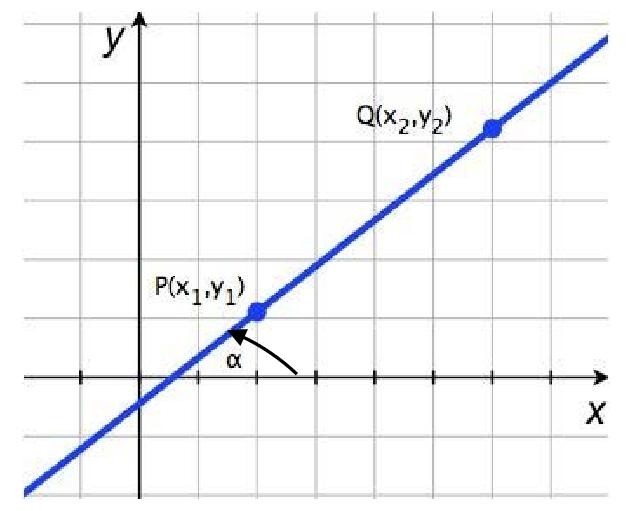
Угловой коэффициент прямой рассчитывают с помощью уравнения:
где \(A\left( <
Уравнение прямой по точке и угловому коэффициенту имеет вид:
где k – является угловым коэффициентом, а точка \(P\left( <
Направляющий вектор прямой, координаты направляющего вектора прямой
С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Как вычислить координаты направляющего вектора по уравнениям прямой
1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
Решение
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
Решение
Решение
А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:
Получившееся равенство преобразовываем и получаем:
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Решение
Решение
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Решим задачу, в которой применяется этот подход.
Решение
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.