Что называется направленным отрезком вектором

Векторы. Виды векторов

Вектором называется направленный отрезок прямой евклидова пространства, у которого один конец (точка A) называется началом вектора, а другой конец (точка B) концом вектора (Рис. 1). Векторы обозначаются:

Если начало и конец вектора совпадают, то вектор называется нулевым вектором и обозначается 0.

Длина отрезка AB называется модулем ( длиной, нормой) вектора и обозначается | a|. Вектор длины, равной единице, называется единичным вектором. Кроме модуля вектор характеризуется направлением: вектор имеет направление от A к B. Вектор называется вектором, противоположным вектору .

Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. На рисунке Рис. 3 красные векторы коллинеарны, т.к. они лажат на одной прямой, а синие векторы коллинеарны, т.к. они лежат на параллельных прямых. Два коллинеарных вектора называются одинаково направленными, если их концы лежат по одну сторону от прямой, соединяющей их начала. Два коллинеарных вектора называются противоположно направленными, если их концы лежат по разные стороны от прямой, соединяющей их начала. Если два коллинеарных вектора лежат на одной прямой, то они называются одинаково направленными, если один из лучей, образованным одним вектором полностью содержит луч, образованным другим вектором. В противном случае векторы называются противоположно направленными. На рисунке Рис.3 синие векторы одинаково направлены, а красные векторы противоположно направлены.

Векторы называются компланарными, если они лежат на одной плоскости или в параллельных плоскостях.

В n мерном векторном пространстве рассмотрим множество всех векторов, начальная точка которых совпадает с началом координат. Тогда вектор можно записать в следующем виде:

Вектор, записанный в виде (1) называется вектор-строкой, а вектор, записанный в виде

Число n называется размерностью ( порядком) вектора. Если то вектор называется нулевым вектором (т.к. начальная точка вектора ). Два вектора x и y равны тогда и только тогда, когда равны их соответствующие элементы:

Сложение векторов

Суммой x+ y векторов x и y называется вектор, проведенный из начала x к концу у, если вектор у параллельно перемещен так, что конец x и начало y совмещены.

Умножение вектора на число

Произведением вектора x на число β ( x≠0, β≠0) называется вектор, модуль которого равен | x|| β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β x=0 и (или) β=0, то βx=0.

Ортогональность векторов

Два вещественных вектора называются ортогональными, если они удовлетворяют соотношению

Источник

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Источник

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Направленные отрезки. Понятие вектора

Определение. Отрезок AB называется направленным, если указано, какая из точек A или B является его началом, а какая концом.

Определение. Длиной направленного отрезка называется длина отрезка AB.

Определение. Направленные отрезки и называются сонаправленными (противоположно направленными), если лучи AB и A₁B₁ сонаправлены (противоположно направлены). Пишем ­­ (­¯).

Определение. Два направленных отрезка и называются эквивалентными или равными, если они сонаправлены и имеют одинаковую длину. Пишем

Û они совмещаются параллельным переносом.

Легко проверить, что данное отношение, определенное на множестве всех направленных отрезков плоскости или пространства обладает следующими свойствами:

Таким образом, отношение, которое мы определили, действительно является отношением эквивалентности (это отношение изучается в курсе алгебры). Поэтому множество всех направленных отрезков распадается на непересекающиеся классы эквивалентных друг другу отрезков.

Предложение 1. Пусть задан направленный отрезок и произвольная точка A₁. Тогда существует одна и толькоодна точка B₁, такая что

. Другими словами, данный вектор можно отложить из любой точки, и притом,единственным образом.

Упражнение. Доказательство проведите самостоятельно

Пример. Пусть ABCD – парал­лело­грамм. Тогда

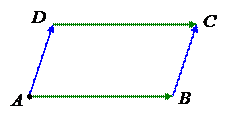
, и поэтому эти направленные отрезки они задают один и тоже вектор. Аналогично и задают один и тот же вектор.

Операции над векторами.

Этот способ построения суммы двух векторов называется правилом треугольника.

Источник

Определения направленного отрезка и вектора

Векторы на плоскости и в пространстве

Определение 1. Направленным отрезком называется упорядоченная пара точек (на плоскости или в трёхмерном пространстве).

Если даны две точки A и B (рассматриваемые именно в этом порядке), то соответ­ствующий направленный отрезок будем обозначать (A, B). Отрезок (в обычном смысле), соединяющий точки A и B, будем обозначать AB. Я не исключаю случая, когда A = B (т. е. можно рассматривать направленный отрезок вида (A, A)). В этом случае отрезок AB пре­вращается в точку. Упорядоченность пары означает, что направленные отрезки (A, B) и (B, A) считаются различными, если A ≠ B.

Определение 2. В направленном отрезке (A, B) точка A называется началом, а точка B − концом.

В направленном отрезке (A, A) начало совпадает с концом.

Определение 3. Направленный отрезок, начало которого совпадает с концом, на­зывается нулевым направленным отрезком.

Определение 4. Если A ≠ B, то (единственную) прямую, проходящую через точки A и B, будем называть несущей прямой (направленного отрезка (A, B)).

В случае A = B несущая прямая не определена однозначно.

Определение 5. Два направленных отрезка (A, B) и (C, D) называются эквивалент­ными (обозначение: (A, B)

1. Их несущие прямые параллельны или совпадают.

2. Длины соответствующих отрезков равны (|AB| = |CD|).

3. Данные направленные отрезки сонаправленны.

Если хотя бы один из направленных отрезков нулевой, то надо опустить первый и третий пункты (можно считать, что они в этом случае всегда выполняются).

Для любителей математической строгости приведу другой вариант определения эквивалентности направленных отрезков, вполне равносильный первому[1]. Он не содержит интуитивного и трудно аксиоматизируемого понятия сонаправленности. Введём такое обозначение: если даны две точки A и B, то середину отрезка, соединяющего точки A и B, будем обозначать med AB (если точки A и B совпадают, то med AB = A)[2].

Определение 6. Два направленных отрезка (A, B) и (C, D) называются эквивалент­ными, если med AD = med BC.

Упражнение. Докажите эквивалентность (равносильность) этих двух определений.

Определение 7. Множество всех направленных отрезков, эквивалентных какому-нибудь одному, называется вектором.

Ясно, что все направленные отрезки из этого множества можно получить из дан­ного с помощью сдвига, или параллельного переноса.

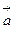
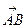
Векторы будем обозначать латинскими курсивными буквами со стрелками, напри­мер, . В печатных текстах принято другое обозначение − латинскими курсивными бук­вами, выделяемыми полужирным шрифтом (иногда тоже стрелками без выделения), на­пример, a. (Я буду здесь так же выделять обозначение вектора полужирным шрифтом.) Если же надо обозначить вектор, соответствующий направленному отрезку (A, B) (т. е. множество всех направленных отрезков, ему эквивалентных), то пользуются другим обо­значением: .

Предложение. Нулевой направленный отрезок эквивалентен другому направлен­ному отрезку тогда и только тогда, когда второй отрезок также нулевой.

Доказательство. Это очевидное следствие любого из двух определений.

Определение 8. Множество всех направленных отрезков, эквивалентных какому-нибудь (а следовательно, и любому) нулевому, называется нулевым вектором и обознача­ется 0.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник