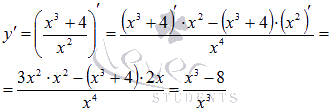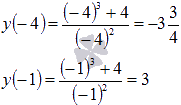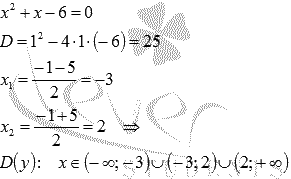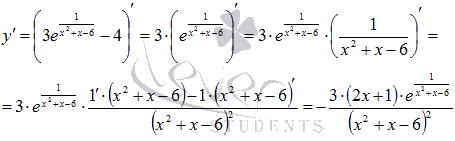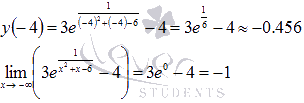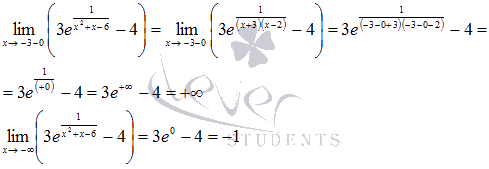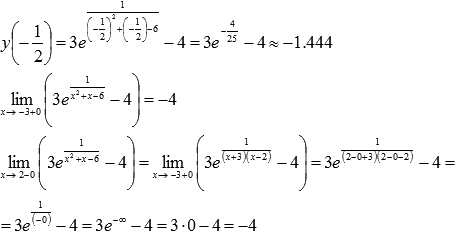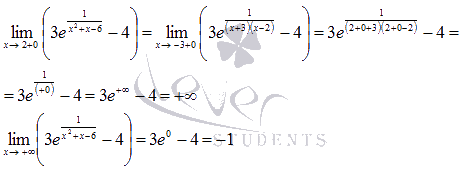Что называется наибольшим и наименьшим значением функции
Наибольшее и наименьшее значение функции.
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Навигация по странице.
Кратко остановимся на основных определениях.
Наибольшим значением функции y=f(x) на промежутке X называют такое значение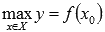 
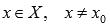
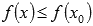
, что для любого 
справедливо неравенство 
.
Наименьшим значением функции y=f(x) на промежутке X называют такое значение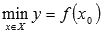 
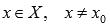
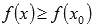
, что для любого справедливо неравенство 
.
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе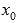 
.
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
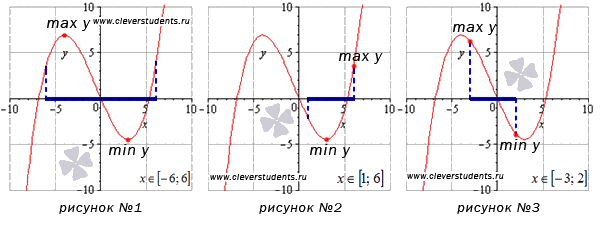
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
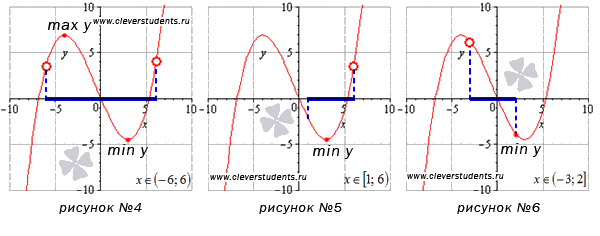
На открытом интервале
На интервале [1;6) наименьшее значение функции достигается в стационарной точке, а про наибольшее значение мы ничего сказать не можем. Если бы точка x=6 была частью интервала, тогда при этом значении функция принимала бы наибольшее значение. Этот пример изображен на рисунке №5.
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть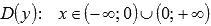 
. Оба отрезка попадают в область определения.
Находим производную функции по правилу дифференцирования дроби:
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1] (так как он не содержит ни одной стационарной точки):
Следовательно,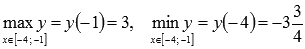 
.
Прежде чем ознакомиться с алгоритмом нахождения наибольшего и наименьшего значения функции на открытом или бесконечном интервале рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.
Проверяем, является ли интервал X подмножеством области определения функции.
Находим все точки, в которых не существует первая производная и которые содержатся в интервале X (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.
Вычисляем значения функции в стационарных точках и точках, в которых не существует первая производная функции (если такие точки есть).
Делаем выводы, отталкиваясь от полученных значений функции и пределов. Здесь может быть масса вариантов. К примеру, если односторонний предел равен минус бесконечности (плюс бесконечности), то о наименьшем (наибольшем) значении функции ничего сказать нельзя для данного интервала. Ниже разобраны несколько типичных примеров. Надеемся подробные описания их решения помогут Вам усвоить тему. Рекомендуем вернуться к рисункам с №4 до №8 из первого раздела этой статьи.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
Очевидно, производная существует на всей области определения функции.
Для первого промежутка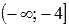 
вычисляем значение функции при x=-4 и предел на минус бесконечности:
Второй интервал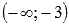 
интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к минус трем слева, мы лишь сможем определить интервал значений функции:
Следовательно, значения функции находятся в интервале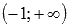 
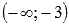
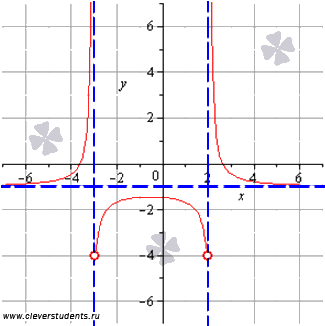
при x из промежутка .
Для интервала (-3;2) воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к двойке слева:
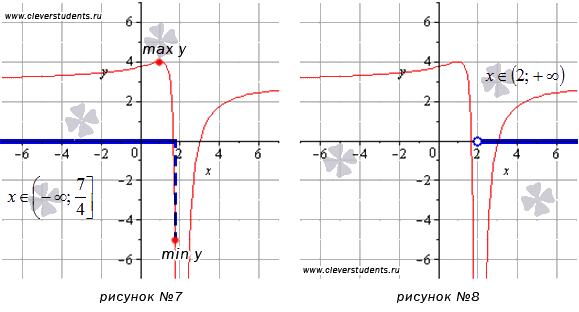
На промежутке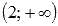 
функция не достигает ни наибольшего, ни наименьшего значения.
То есть, на этом интервале функция принимает значения из промежутка .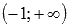
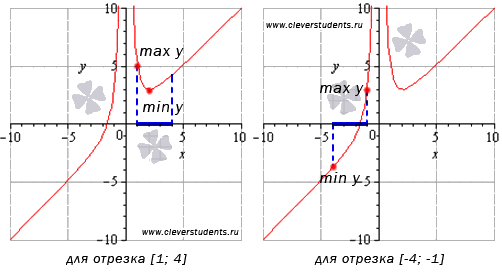
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.
Наибольшее и наименьшее значения функции
Вы будете перенаправлены на Автор24
Понятие наибольшего и наименьшего значений функции.
Понятие набольшего и наименьшего значений тесно связано с понятием критической точки функции.
Введем теперь определения наибольшего и наименьшего значения функции.
Теорема Вейерштрасса о непрерывной на отрезке функции
Введем для начала понятие непрерывной на отрезке функции:
Сформулируем теорему о непрерывной на отрезке функции.
Готовые работы на аналогичную тему
Геометрическая интерпретация теоремы изображена на рисунке 1.
6) Выбрать из полученных значений наибольшее и наименьшее значение.
Задачи на нахождение наибольшего и наименьшего значений функции на отрезке
Решение.
Решение будем проводить по выше данной схеме.
\[f\left(0\right)=1\] \[f\left(2\right)=16-60+72+1=29\] \[f\left(3\right)=54-135+108+1=28\] \[f\left(4\right)=128-240+144+1=33\]
Решение.
Решение будем проводить по выше данной схеме.
\[f\left(0\right)=225\] \[f\left(5\right)=125-75-225+225=50\] \[f\left(6\right)=216-108-270+225=63\]
Решение.
Решение будем проводить по выше данной схеме.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 10 03 2021
Основные свойства функций. Справочник репетитора по математике
Д анная страница справочника представляет собой виртуальную шпаргалку по математике для учеников и методическое справочное пособие для репетиторов. Тема «свойства функций», адаптированное для разных уровней учащихся 8-9класов. В нем перечислены определения основных понятий и свойств, виды функций, термины и обозначения, принятые в математике. Репетитору по математике показаны образцы рисунков, которые должны остаться в теради ученика. Информация изложена как на строгом и формальном математическом языке (для среднего и сильного ученика), так на простом (бытовом) уровне, доступном для понимания широкому кругу посетителей сайта. Каждый такой перевод с математического языка на русский отмечен одним из следующих указателей: «пояснение репетитора по математике», «редакция репетитора по математике» или «уточнение репетитора по математике». В этих — переводах вы встретите несколько моих собственных уникальных дополнений и комментариев к классическим фомулировкам, которые я использую на занятиях со слабым учеником.
Определение функции: функцией или функциональной зависимостью называется такое соответствие f (x) при котором числу x из множества X сопоставляется некоторое единственное число из множества Y.
Редакция репетитора по математике: функцией называется закон или правило, по которому можно найти число y (значение какой-нибудь величины), если известно число x (значение какой-нибудь другой величины).
При этом букву x называют независимой переменной (или аргументом), а букву y — зависимой переменной. Число, которое подставляется вместо x, называется значением переменной (или значением аргумента), а число y, которому оно соответствует, называется значением функции.
График функции — множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Свойства функции:
1) Что такое область определения функции? Область определения функции (О.О.Ф) — это множество всех значений переменной x, которые имеют соответствующие им значения функции.
Редакция репетитора по математике: область определения — множество значений переменной x, у которых можно найти y.
Обозначения области определения Для обозначения области определения используются следующие знаки: 
Как найти область определения по графику? Область определения — это промежутки на оси Ох, над которыми (или под которыми) имеются части графика.
2) Что такое область значений функции? Областью значений функции (О.З.Ф) называется множество всех ее значений.
Редакция репетитора по математике:областью значений функции можно назвать часть оси ОY, состоящую из игреков, у которых есть соответствующие им иксы.
Как найти область значений по графику?: область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полоске) находятся части графика.
3) Возрастание и убывание функции.
Какая функция называется возрастающей?Функция 
называется возрастающей, если для любой пары значений аргументов 
и 
из неравенства 
следует неравенство 
.
Редакция репетитора по математике: Функцию можно назвать возрастающей на промежутке, если, большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Для графика это будет означать то, что при движении по нему карандашом слева направо карандаш будет подниматься вверх.
Какая функция называется убывающей? Функция называется убывающей, если для любой пары значений аргументов и из неравенства следует неравенство 
f (x_2)’ style=’vertical-align:-30%’ alt=’f (x_1)>f (x_2)’ />.
Редакция репетитора по математике: Функцию можно назвать убывающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует меньшее значение функции. Для графика это будет означать, что при движении по нему карандашом слева направо карандаш будет опускаться вниз.
Можно предложить еще один вариант этого определения: функция называется возрастающей на промежутке, если знак которым связаны любые два числа ее области определения, противоположен тому, которым связаны соответствующие им значения функции.
4) Промежутки знакопостоянства — промежутки, на которых функция имеет постоянный знак (положительный или отрицательный).
Пояснения репетитора по математике: Промежуток положительного знака — это множество значений переменной x, у которых соответствующие значения функции больше нуля (y>0 ).
Как найти все такие промежутки по графику? Определите промежутки оси ОХ, у которых соответствующие кусочки графика выше оси Ох.
Как их найти без графика? составьте и решите неравенство f (x)>0
Оформление: 
o ‘ style=’vertical-align:-5%’ alt=’y>o ‘ />, если 
Промежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y
Наибольшее и наименьшее значение функции
Теория к заданию 12 из ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
Чтобы найти точки максимума или минимума необходимо:
Таблица производных некоторых элементарных функций:
| Функция | Производная |
| $c$ | $0$ |
| $x$ | $1$ |
| $x^n, n∈N$ | $nx^ |
| $<1>/ | $-<1>/ |
| $<1>/x<^n>, n∈N$ | $- |
| $√^n | $<1>/ |
| $sinx$ | $cosx$ |
| $cosx$ | $-sinx$ |
| $tgx$ | $<1>/ |
| $ctgx$ | $-<1>/ |
| $cos^2x$ | $-sin2x$ |
| $sin^2x$ | $sin2x$ |
| $e^x$ | $e^x$ |
| $a^x$ | $a^xlna$ |
| $lnx$ | $<1>/ |
| $log_x$ | $<1>/ |
Основные правила дифференцирования
1. Производная суммы и разности равна производной каждого слагаемого
Производная суммы и разности равна производной каждого слагаемого