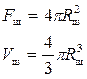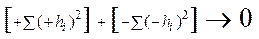Что называется моделью земли

Кто и когда придумал глобус Земли

«Земное яблоко» диаметром 54 сантимера до сих пор хранится в музее

В произведениях античных писателей упоминается о том, что первый глобус был создан примерно в 150 году до нашей эры Кратетом Малльским – древнегреческим философом и последователем Аристотеля. Правда, до наших дней не дошли даже её изображения. Известно, что астроном из Бухары Джамаль ад-Дин в 1267 году в Ханбалыке преподнёс хану Хубилаю в качестве подарка от хана Хулагу глобус, астролябию и армиллярную сферу.

Османский учёный Такиюддин аш-Шами сконструировал современный вид глобуса для своей стамбульской обсерватории примерно в 1574 году. Но самым старым из всех сохранившихся глобусов считается шарообразная модель Земли диаметром 54 сантиметра, созданная немецким географом, путешественником и математиком Мартином Бехаймом в 1492 году. Она до сих пор хранится в музее немецкого города Нюрнберга.

На «Земном яблоке», как назвал его Бехайм, были отражены географические представления о поверхности Земли накануне открытия Нового Света, основывавшиеся на данных, взятых с карт мира древнегреческого учёного Птолемея, жившего во II веке. Вскоре после этого глобусы, дающие наиболее точные картографические представления и пользующиеся большим спросом у учёных и моряков, стали настоящим символом просвещения.

Особенно популярны были нидерландские глобусы, которые делали амстердамские мастера Блау. Они создали модель Земли, которая была подарена русскому царю Алексею Романову в 1672 году – впервые на Руси. Самой известной из всех зарубежных моделей земного шара является Готторпский глобус диаметром 311 сантиметров, изготовленный немецким учёным Адамом Ольшлегелем в 1664 году и в 1713 подаренный Петру I.

Читайте главные новости дня на ленте «Популярной механики» в Telegram

Источник

2.2 Конспект для ученика по теме «Географические модели»

В статье рассматривается вопрос «Географические модели. Географическая карта, план местности». Материал стати актуален для подготовки к ЕГЭ.

Географические модели

Поверхность Земли невозможно изобразить на бумаге, из-за её больших размеров, поэтому её изображают в виде моделей.

К моделям Земли или поверхности относят:

Наиболее точно изображена поверхность планеты на глобусе:

Изображение Земли на карте

Чтобы изобразить поверхность земли на карте используется градусная сетка: это параллели и меридианы, расположенные перпендикулярно друг к другу.

Параллели расположены горизонтально (параллельно экватору), меридианы вертикально протягиваются от северного полюса до южного.

Для удобства определили нулевой меридиан (Гринвичский) от которого идут меридианы на расстоянии 10° друг от друга, т.е. нулевой меридиан является началом полушарий, который протягивается до 180°( меридиан 180° является границей полушарий).

На восток считается восточная долгота, на запад – западная. Параллели также идут на расстоянии 10°. Для удобства экватор выбран нулевой параллелью.

К северу отсчитывается северная широта, к югу – южная. С помощью градусной сетки можно наносить объекты на карту, а также находить их месторасположения, то есть координаты. Для определения координат необходимо знать долготу и широту местности.

Географические координаты

Виды карт

Карты отличаются друг от друга по нескольким критериям:

Масштаб бывает численный, линейный (используется при измерении расстояния от точки А до точки В) и именованный.

Чем мельче масштаб карты, тем большую территорию на ней можно изобразить. Карты полушарий, материков и океанов, карты государств это мелкомасштабные карты. Среднемасштабные карты в пределах от 1:200000 до 1:1000000. И крупномасштабные (топографические) карты (1:10 000, 1:25 000 и 1: 50 000).

По содержанию карты бывают:

Карты также бывают комплексные, синтетические и аналитические. Комплексные карты несут множество информации об изображенной местности. На синтетических картах показано целостное изображение, но не дается представления об отдельных объектах местности. На климатической карте изображены типы климатов, но мы не узнаем из этой карты ни температуры, ни господствующих ветров. Аналитические карты дают представление об одной характеристике территории, например, о распаханности земель.

Условные обозначения

Для того чтобы уметь читать карту и находить на ней информацию, надо знать условные обозначения и уметь их правильно читать. Все карты изображены с помощью условных знаков. Для каждой карты характерны свой набор знаков. На карте полезных ископаемых, изображен рельеф с помощью изолиний и цветовой окраски. По цветовой окраске мы определяем вид рельефа, изолинии (линии соединяющие точки с одинаковой высотой) дают более точную информацию о высоте поверхности над уровнем или ниже уровня моря. Месторождения полезных ископаемых обозначаются специальными значками.

Графическими условными знаками изображают границы, ареалы, автодороги, направления ветра, течений.

Знаковые – обозначают полезные ископаемые, растительный и животный мир.

Точечные обозначения применяются для обозначения плотности населения, городов.

Цифровыми знаками могут обозначать высоту гор, глубину впадин, года, температуру и т.д.

Буквенными знаками изображают название городов, рек, озер, стран и т.д.

Условные знаки на географических картах

Условные знаки на географических картах передают количественные и качественные характеристики объектов, показывают явления, не воспринимаемые органами чувств (магнитные склонения), области, недоступные взору человека (строение земной коры на больших глубинах), представляют научные понятия, обобщения, абстракции. Чтобы правильно передать нужную информацию на карте картограф должен разбираться в способах отображения.

В настоящее время для передачи содержания на географических картах применяются следующие способы картографического изображения:

Значковый способ

Используют для обозначения находящихся на местности, но не выражающихся в масштабе объектов: населённых пунктов, промышленных и сельскохозяйственных предприятий, залежей полезных ископаемых и др. Значковый способ чаще применяют на социально-экономических картах. Количественные характеристики передаются величиной значков, их линейными, площадными или объёмными размерами. Качественные характеристики передаются цветом, штриховкой и формой значков.

Используют три вида значков:

Источник

Глобус и карта

1. Какие виды изображения земной поверхности вам известны?
2. Чем отличаются указанные вами виды изображения земной поверхности?

1. Как называется модель Земли и каковы её особенности.
2. Чем отличается географическая карта от глобуса.
3. Какие фотографические изображения позволяют исследовать Землю.

Можно ли карту называть моделью Земли?

Глобус

Посмотрите на глобус. Примерно то же самое видят космонавты, находящиеся на околоземной орбите. Гло́бус — модель земного шара. Он наиболее правильно отображает форму нашей планеты. На нём в очень уменьшенном виде изображены все имеющиеся на поверхности Земли крупные объекты: материки и океаны, острова и полуострова, моря и заливы (рис. 13). Всю поверхность Земли можно увидеть, повернув глобус всего лишь один раз. Глобус очень удобен для того, чтобы представить себе форму и облик поверхности нашей планеты, но в некоторых случаях, он не слишком-то годится. Глобус — предмет довольно громоздкий, он не складывается, и в карман его не положить. Его невозможно взять с собой в поход. Да и трудно представить, например, лётчика, который крутит перед собой в кабине глобус. Карта удобнее, да к тому же на ней отражено больше разной информации, чем на глобусе.

Глобус — модель земного шара. Глобус очень удобен для того, чтобы представить себе форму и облик поверхности нашей планеты.

Географическая карта

Первые карты представляли собой рисунки, изображавшие какую-либо местность, а иногда и целые страны (рис. 14). Давайте сравним изображения на рисунке и на географической карте, например на форзаце учебника. Мы увидим, что на старинной карте всё изображалось, как есть: город — это группа домиков, лес — группа деревьев и т.д. Но из-за того, что каждый видит мир по- своему, рисунки получались разные. В результате рисованными картами не очень удобно было пользоваться. Прошло немало веков, прежде чем люди придумали простые, понятные всем способы изображения разных объектов на карте. Карты перестали быть рисунками, а превратились в чертежи, понять которые может любой человек, который умеет читать карту. Ка́рта — это чертёж, изображающий поверхность Земли в уменьшенном виде.

Есть карты, на которых уместились страны, материки и даже вся поверхность Земли. На картах могут быть изображены и совсем небольшие участки местности, но зато очень подробно. Такие изображения называют топографи́ческими картами и пла́нами ме́стности. Об отличиях между ними мы поговорим в б классе.

Карта — это чертёж, изображающий поверхность Земли в уменьшенном виде.

Физическая карта мира

В 5 классе вам предстоит в основном встречаться с одной картой — физической картой мира. Давайте познакомимся с ней поближе (см. форзац 1).

На физической карте мира изображается весь земной шар. Это очень хорошо, ведь на ней можно увидеть все материки и все океаны. С её помощью мы сможем изучать историю географических открытий и природу материков.

Но есть и сложности. В чём разница между глобусом и картой? Глобус — шарообразная модель Земли, а карта — плоский чертёж. Изображено на них одно и то же — поверхность Земли. Как мы уже знаем, Земля имеет форму шара и изобразить её на бумаге без искажений невозможно. Поэтому по сравнению с глобусом изображение на карте искажено. Особенно заметны эти искажения на карте в северной части Тихого океана. Видите? Там контуры Евразии и Северной Америки растянуты. К этому нужно привыкнуть и не забывать об искажениях.

Источник

ФОРМА ЗЕМЛИ И ЕЕ МОДЕЛИ

ОРИЕНТИРОВАНИЕ НА МОРСКОЙ ПОВЕРХНОСТИ ЗЕМЛИ

Глава 1

ОСНОВНЫЕ ПОНЯТИЯ НАВИГАЦИИ

РАЗДЕЛ 1

Навигация (от лат. navigation – мореплавание) – это математическая наука о способах определения оптимального пути судна на водной поверхности Земли и о способах прокладки этого пути на морской навигационной карте (от лат. optimus – наилучший).

Морская навигационная карта (сокращенно МНК) – это плоское изображение выпуклой поверхности морей и океанов с прилегающими участками суши в виде береговой полосы.

Перенос выпуклой поверхности Земли на плоскость производится путем математических вычислений.

Прокладка пути судна производится путем решения геометрических задач на водной поверхности Земли и на карте.

Математические вычисления по переносу выпуклой поверхности Земли на карту и решение геометрических задач по прокладке пути судна на водной поверхности Земли и на карте возможны только в том случае, если планета Земля является геометрическим телом.

Геометрическое тело – это объемная фигура простой формы, которая поддается математическому описанию, когда форму и размеры этого тела можно выразить с помощью простых математических формул.

В качестве примера можно привести геометрическую фигуру шар, который имеет наиболее простую форму, т.к. все точки поверхности шара одинаково удалены от его центра. Поэтому форму и размер шара определяет один параметр – радиус шара (от греч. parametron – отмеривающий).

К размерам шара относится площадь поверхности шара (F_ш) и объем шара (V_ш), которые вычисляются с помощью известных формул:

В математике площадь объемной фигуры называют поверхностью. Например, площадь шара – это поверхность шара.

Планета Земля, созданная 4.7 миллиардов лет назад из газово-пылевого космического вещества, имеет очень сложную форму, которая не поддается математическому описанию. Поэтому возникает необходимость аппроксимации (замены) планеты Земля геометрическим телом, которое называется геометрической (математической) моделью Земли.

Аппроксимацию планеты Земля (от лат. approximo – приближаюсь) производят путем последовательного приближения внешнего контура Земли к форме геометрического тела:

­ сначала создают физическую модель Земли, которой является фигура планеты Земля, более простой формы. Поэтому эта модель получила название геоид, что в переводе с греческого языка – вид Земли (от греч. слов ge – Земля и iodos – вид);

­ на базе геоида создают геометрическую модель Земли – эллипсоид, форма и размеры которого наиболее близки форме и размерам геоида. Поэтому этот эллипсоид называется земным эллипсоидом или референц-эллипсоидом (от лат. referens – сообщающий – часть сложного слова, которая определяет, что референц-эллипсоид является носителем информации о форме и размерах Земли);

­ на базе земного эллипсоида создают геометрическую модель Земли – шар, размеры которого наиболее близки размерам земного эллипсоида. Поэтому этот шар называется земным шаром.

Принцип создания геоида основан на «сглаживании» физической поверхности планеты Земля с целью получения фигуры более простой формы.

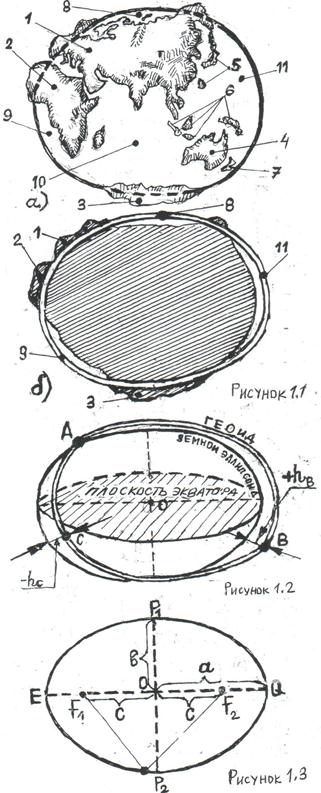
Физическая поверхность Земли (от греч. physika – природа) – это наружная оболочка планеты Земля, которая состоит из двух сфер (рисунок 1.1):

1. Гидросфера (от греч. hydor – вода) – это наружная водная оболочка Мирового океана (8-11), которая окружает материки и острова (1-7) и занимает около 71% земной поверхности.

2. Литосфера (от греч. lithos – камень) – это твердая часть поверхности Земли, которая состоит из материковой и океанической земной коры и верхней мантии (мантия Земли – это оболочка, расположенная между земной корой и ядром Земли).

«Сглаживание» физической поверхности планеты Земля производят путем удаления с этой поверхности той части литосферы, которая возвышается над уровнем Мирового океана в виде материков и островов.

Таким образом, геоид – это фигура планеты Земля, ограниченная гидросферой, над которой не возвышается литосфера Земли. На рисунке 1.1 «б» фигура геоида показана в разрезе с помощью двойной овальной кривой.

Однако сглаженная поверхность геоида тем не менее имеет сложную форму. Поэтому геоид не является геометрической фигурой. Наиболее близкой по форме к геоиду является геометрическая фигура эллипсоид, поверхность которого имеет наибольшее совмещение с поверхностью геоида (рисунок 1.2).

Эллипсоид – это геометрическая объемная фигура, которая образована вращением плоской фигуры под названием эллипс.

Эллипс – это овальная кривая, которая образована сжатием окружности, в результате чего эллипс имеет вытянутую большую ось ЕQ и укороченную малую ось Р₁Р₂ (рисунок 1.3).

Форму и размер эллипса определяют следующие параметры (рисунок 1.3):

­ длина большой полуоси эллипса «a»;

­ длина малой полуоси эллипса «b»;

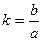
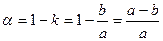
­ коэффициент сжатия эллипса и сжатие эллипса ;

­ эксцентриситет эллипса ε;

­ отстояние фокусов эллипса F₁ и F₂ от центра этого эллипса, которое обозначено буквой «с».

Эксцентриситет эллипса (ε) – это число, равное отношению расстояния между фокусами эллипса к длине большой оси эллипса. Поскольку расстояние между фокусами равно 2с, а длина большой оси равна 2а, то .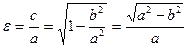

Фокусы эллипса – это точки F₁ и F₂ на большой оси эллипса, сумма расстояний от которых до любой точки эллипса равна длине большей оси этого эллипса:

,

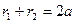
где 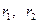— расстояние любой точки эллипса до фокусов, которые называются фокальными радиусами точки эллипса.

Эллипсоид, образуемый вращением эллипса вокруг большой оси EQ, называется вытянутым эллипсоидом.

Эллипсоид, образуемый вращением эллипса вокруг малой оси Р₁Р₂, называется сжатым эллипсоидом или сфероидом.

В качестве математической модели Земли применяют сжатый эллипсоид и поэтому земной эллипсоид имеет еще один синонимичный термин – земной сфероид (от греч. synonymos – одноименный).

Земной эллипсоид (земной сфероид или референц-эллипсоид) имеет следующие параметры, которые определяют его форму и размеры:

— длина большой полуоси эллипсоида «a»;

— длина малой полуоси эллипсоида «b»;

— полярное сжатие эллипсоида ;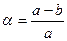

— величина первого эксцентриситета эллипсоида 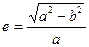, которая равна величине эксцентриситета эллипса, вращением которого получен данный эллипсоид.

Принцип создания земного эллипсоида основан на вычислении таких значений параметров a, b, 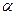и е, при которых эллипсоид приобретает форму и размеры, близкие форме и размерам геоида. Основным признаком близости земного эллипсоида и геоида по форме и размерам является наибольшее совпадение поверхностей этих фигур (рисунок 1.2).

Форма и размеры земного эллипсоида наиболее близки форме и размерам геоида при соблюдении следующих условий (рисунок 1.2):

1. Объем земного эллипсоида должен быть равен объему геоида.

2. Малая ось земного эллипсоида должна совпадать с осью вращения Земли.

3. Плоскость экватора земного эллипсоида должна совпадать с плоскостью экватора геоида.

4. Алгебраическая сумма квадратов геодезической высоты всех точек геоида должна быть наименьшей.

Плоскость экватора земного эллипсоида – это плоскость сечения, которая проходит через центр этого эллипсоида под углом 90º к оси вращения Земли.

Если совместить 2 фигуры – геоид и земной эллипсоид, то поверхность геоида на каком-либо участке может совпадать с поверхностью земного эллипсоида, либо возвышаться над поверхностью земного эллипсоида, либо находиться ниже. На рисунке 1.2 поверхности обеих фигур совмещены в точке А, а точка В геоида находится над поверхностью земного эллипсоида и точка С расположена ниже поверхности земного эллипсоида.

Геодезическая высота точки геоида (h) – это высота какой-либо точки поверхности геоида относительно поверхности земного эллипсоида, которая может иметь следующие значения (рисунок 1.2):

— нулевая геодезическая высота точки А (h_A=0) – когда точка А является точкой соприкосновения геоида и земного эллипсоида;

— положительная геодезическая высота точки В (+h_B) – когда точка В находится над поверхностью земного эллипсоида;

— отрицательная геодезическая высота точки С (-h_C) – когда точка С находится под поверхностью земного эллипсоида.

Чтобы обеспечить наибольшее совпадение поверхностей геоида и земного эллипсоида – алгебраическая сумма геодезических высот всех точек геоида, возведенных в квадрат, должна быть наименьшей, т.е. стремиться к нулю:

Таким образом, земной эллипсоид (земной сфероид, референц-эллипсоид) – это геометрическая объемная фигура эллипсоид, форма и размеры которой наиболее близки к форме и размерам геоида. Поэтому земной эллипсоид является геометрической (математической) моделью Земли, которую применяют в качестве математической основы для решения следующих задач:

1. Математическое построение морской навигационной карты (МНК).

2. Определение местоположения судна на водной поверхности Земли.

3. Определение направления движения судна и пройденного судном расстояния и для решения других навигационных задач.

Начиная с 1830 года, было создано множество земных эллипсоидов, параметры которых вычисляли какие астрономы и геодезисты, как Эри (Англия), Бессель (Германия), Кларк (Англия), Хейфорд (США), Красовский (СССР) и многие другие (таблица 1.1).

Название земного эллипсоида	Год	а	b		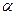e
Эллипсоид Эри	6 377 563	6 356 257	1/299.325	0.081 672 445
Эллипсоид Бесселя	6 377 397	6 356 079	1/299.1528	0.081 672 464
Эллипсоид Кларка	6 378 206	6 356 585	1/294.9787	0.082 268 817
Эллипсоид Хейфорда	6 378 388	6 356 912	1/297.0	0.081 991 787
Эллипсоид Красовского	6 378 245	6 356 863	1/298.3	0.081 813 336
WGS-84	6 378 137	6 356 752	1/298.2572	0.081 819 791
ПЗ-90 (PE-90) или SGS-90	6 378 136	6 356 751	1/298.2578	0.081 819 797

Анализ таблицы 1.1 показывает, что земные эллипсоиды разных авторов имеют разную форму и размеры, т.к. значения параметров этих эллипсоидов отличаются на величину до одного километра. Это объясняется тем, что каждый земной эллипсоид имеет свою точку привязки к геоиду, которая является исходной точкой для вычисления параметров этого эллипсоида.

Точкой взаимной привязки геоида и земного эллипсоида является точка соприкосновения поверхностей этих фигур, в окрестностях которой поверхности земного эллипсоида и геоида совпадают наиболее точно. Поэтому каждая страна использует для создания карт тот земной эллипсоид, который имеет наилучшее приближение к поверхности геоида на территории этой страны.

Таким образом, эллипсоид, который применяют в качестве математической основы при составлении карт территории какой-либо страны принято называть национальным геодезической системой (National Geodetic System NGS). Так, например, до 1946 года национальной геодезической системой России и Украины был земной эллипсоид Бесселя. В 1942 году под руководством профессора Московского научно-исследовательского института геодезии Красовского Феодосия Николаевича был создан земной эллипсоид, поверхность которого имеет лучшее приближение к геоиду на территории России и Украины, нежели поверхность эллипсоида Бесселя, т.к. точкой взаимной привязки эллипсоида Красовского и геоида является центр круглого зала Пулковской астрономической обсерватории вблизи Санкт-Петербурга (Геодезия – от греч. слов ge – Земля и daio – разделяю: наука о форме и размерах Земли. Астрономия – от греч. слов astron – звезда и nomos – закон. Обсерватория – от лат. observatio – наблюдение). Поэтому в настоящее время в России и в Украине для составления морских навигационных карт используют национальную геодезическую систему «Пулково-42», которая является эллипсоидом Красовского.

Расчет параметров орбиты навигационных спутников Земли (от лат. orbita – колея, путь) производят на базе Всемирных геодезических систем, к которым относятся следующие земные эллипсоиды:

— Параметры Земли 1990 года – ПЗ-90 (Parameter of Earth of 1990 year – PE-90) или Советская геодезическая система 1990 года (Soviet Geodetic Systemof 1990 year – SGS-90) – земной эллипсоид, который является математической основой для расчета параметров орбиты искусственных спутников Земли российской спутниковой радионавигационной системы (СРНС) «ГЛОНАСС» (Глобальная Навигационная Спутниковая Система).

Если сравнить длину большой и малой полуосей любого земного эллипсоида в таблице 1.1, то малая полуось (b) окажется короче большой полуоси (а) в среднем на 21 км, что составляет 0,3% длины большой полуоси. Для наглядности можно изобразить земной эллипсоид в уменьшенном виде так, чтобы его большая полуось равнялась одному метру (а = 1 м), то малая полуось будет короче на 3 миллиметра (b = 0,997 м). При такой незначительной разнице большой и малой осей – земной эллипсоид по форме очень близок шару. Поэтому для решения практических задач навигации, которые не требуют повышенной точности, вполне допустимо применять более простую по форме геометрическую (математическую) модель Земли – шар, размеры которого наиболее близки размерам земного эллипсоида.

Таким образом, земной шар – это шар, размеры которого наиболее близки размерам земного эллипсоида.

Принцип создания земного шара основан на вычислении такого радиуса шара, при котором размеры этого шара будут наиболее близки размерам земного эллипсоида. В зависимости от способа вычисления радиуса шара – созданы следующие модификации земного шара:

1. Земной шар, объем которого равен объему земного эллипсоида.

В этом случае радиус шара определяют из равенства объемов земного шара и земного эллипсоида:

(1.1)

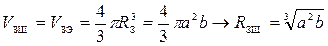
2. Земной шар, поверхность которого наиболее близка поверхности земного эллипсоида. В этом случае радиус земного шара определяют из равенства площадей земного шара и земного эллипсоида:

(1.2)

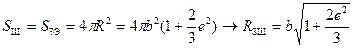
3. Земной шар, радиус которого равен длине большой полуоси земного эллипсоида: R_ЗШ = а.

Источник