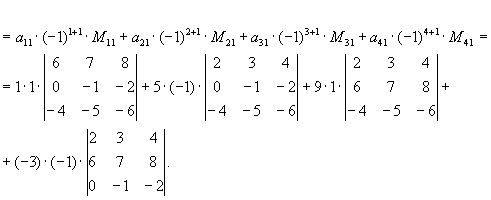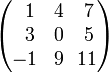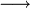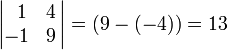Что называется минором элемента матрицы

Что называется минором элемента матрицы

.

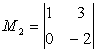
Пример. .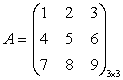

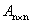
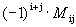
Определение 3. Алгебраическим дополнением A _ij к элементу a _ij квадратной матрицы называется число A _ij = .

Пример. Найдем алгебраическое дополнение к элементу a ₃₃.

.

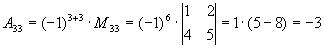
Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.

Теорема 2. Сумма попарных произведений элементов любой строки определителя на алгебраические дополнения к соответствующим элементам другой строки равна нулю.

Вычисление определителей порядка n >3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя.

по первому столбцу

Перед разложением определителя для удобства получают в одном из столбцов нули. Это сокращает объемы вычислений. Для этого используют пятое свойство определителя. Одну из строк умножают на некоторые числа и складывают с другими строками.

Источник

Минор матрицы

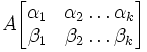
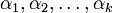
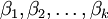
Минор матрицы A ― определитель матрицы, элементы которой стоят в данной прямоугольной матрице порядка k (который называется также порядком этого минора) на пересечении строк с номерами и столбцов с номерами .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым или ведущим главным.

Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.

Пример

Например, есть матрица:

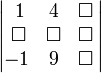
См. также

Полезное

Смотреть что такое «Минор матрицы» в других словарях:

Минор (математич.) — Минор (от лат. minor меньший) k го порядка матрицы, определитель, составленный из элементов, стоящих на пересечении произвольно выделенных k строк и k столбцов матрицы. Так, определитель есть М. 2 го порядка матрицы составленный из ее элементов,… … Большая советская энциклопедия

МИНОР — определитель, составленный из элементов, состоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Большой Энциклопедический словарь

МИНОР (в математике) — МИНОР, определитель, составленный из элементов, состоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Энциклопедический словарь

МИНОР — 1. М. элемента aij определителя А есть определитель, полученный из А после вычеркивания элементов i ой строки и j гo столбца. М. m го порядка матрицы А ||aij|| есть определитель m го порядка, составленный из m2 элементов, стоящих на пересечении… … Геологическая энциклопедия

Минор — [minor] см. Определитель матрицы … Экономико-математический словарь

Минор (линейная алгебра) — У этого термина существуют и другие значения, см. Минор (значения). Минор матрицы ― определитель такой квадратной матрицы порядка (который называется также порядком этого минора), элементы которой стоят в матрице на пересечении строк с номерами … Википедия

Минор — I Минор Лазарь Соломонович [17(29).12.1855 1942], советский невропатолог, заслуженный деятель науки РСФСР (1927). В 1879 окончил медицинский факультет Московского университета, работал у А. И. Бабухина, А. Я. Кожевникова. В 1910 17… … Большая советская энциклопедия

минор — а; м. [от итал. minore меньший]. 1. Музыкальный лад, звуки которого образуют аккорд, построенный на малой трапеции (характеризуется звуковой окраской, связанной с настроениями грусти, скорби; противоп.: мажор). Играть в миноре. 2. Разг. О… … Энциклопедический словарь

МИНОР — порядка к определитель матрицы, элементы к рой стоят в данной прямоугольной матрице на пересечении кразных столбцов и кразных строк. Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то М. наз. главным, а есля отмечены первые … Математическая энциклопедия

МИНОР — определитель, составленный из элементов, стоящих на пересечении произвольно выделенных k строк и k столбцов данной матрицы или определителя … Естествознание. Энциклопедический словарь

Источник

Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.

Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:

Например, рассмотрим такую матрицу:

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.

Для примера рассмотрим квадратную матрицу пятого порядка:

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Минор матрицы — способы, порядок и примеры вычисления

Одним из ключевых понятий в линейной алгебре является минор матрицы. Зная, что это такое и как его вычислить, определить ранг матриц любого порядка не составит труда. По сути, это определитель, находимый путём убирания из рассматриваемой матрицы вертикальных и горизонтальных полос, на пересечении которых находится элемент aij. Существует несколько видов алгебраических миноров, по значению которых можно судить об обратимости, а значит, и возможности нахождения линейной регрессии.

Общие сведения

При решении систем, состоящих из алгебраических и дифференциальных уравнений, для удобной их записи применяется таблица. Она содержит строки и столбцы, пересечение которых определяется элементами. Количество строк характеризуется числом уравнений, а столбцов — количеством неизвестных величин. После построения такой таблицы решение сводится к работе с ней. Совокупность элементов такой таблицы называют матрицей.

Над несколькими матрицами можно выполнять различные арифметические действия: преобразовывать, умножать, складывать. При этом допускается умножение строки на числа, отличные от нуля, сложение строк между собой и изменение их положения. Обозначают матрицу с помощью заглавной буквы латинского алфавита. Характеризуется она размерностью и может быть квадратной или прямолинейной.

При математической записи используют индексы. Первый из них обозначает строки, а второй — столбцы. На месте их пересечения находится элемент. То есть таблица вида m x n записывается как A = (aij)m, n, где: aij — элемент матрицы, располагающийся на пересечении и-той строки и йо-того столбца. Ранг же матрицы показывает наибольшее число линейно независимых столбцов или строк, при этом он не может превосходить размерность.

Важным параметром квадратной матрицы является определитель (детерминант). При его нахождении используется минор. Существует несколько его разновидностей:

В общем случае под определением минора матрицы понимают определитель, находимый с помощью удаления строки и столбца определённого элемента. При рассмотрении алгебраических дополнений совместно с ними используют понятие угловой минор.

Квадратная матрица

Минор принято разделять на элементный и матричный. Для лучшего понимания сначала следует разобрать минор квадратной матрицы. Рассматривать нужно её, так как минор — это определитель, а он бывает только у квадратной системы уравнений. Параметр элемента матрицы и определителя находят одинаково.

Вычисление минора обычно не вызывает трудностей. При этом стоит помнить простые правила определения детерминанта:

Пусть необходимо определить параметр элемента i, j. Для этого нужно посмотреть на записанную таблицу и выделить и-тую строчку и йо-тый столбец. На их пересечении будет стоять цифра, которая соответствует элементу aij. После вычёркивания элементов, расположенных от него по вертикали и горизонтали, оставшиеся в наборе и будут являться минором матрицы или определителя.

Например, пусть имеется определитель вида:

Нужно найти минор два три. На пересечении второй строчки и третьего столбца стоит цифра минус два. Убрав вторую соответствующую ей вертикаль и третью горизонталь, можно получить искомый минор M23:

Теперь, чтобы найти минор единицы, нужно вычислить определитель полученной матрицы четвёртого порядка. Для этого удобно использовать теорему Лапласа для разложения по любой строке. Выбирать лучше ту, где стоят нули. После преобразования полученный ответ и будет минором. Аналогично выполняют действия и для определителя.

Алгебраическое дополнение элемента находится по формуле: Aij = (-1) i+j * Мij. Это выражение справедливо для любой квадратной матрицы. Для рассматриваемого примера такое дополнение будет равно следующему произведению: A23 = (-1)2+3 * M23 = — M23. Минор и алгебраическое дополнение имеют численные значения. Но при вычислении последнего необходимо учитывать, что сумма произведения определителя на дополнение к элементам будет равняться определителю, а сложение произведений двух элементов столбца или строки даст в ответе ноль.

Главный и базисный определитель

Минором высшего уровня описывают систему, состоящую из столбцов и строк, число которых превышает два. То есть минор восьмого порядка представляет собой определитель, состоящий из восьми столбцов и такого же числа строк. Тут следует отметить, что исходная матрица должна иметь больший порядок.

В таблице высшего порядка можно выделить несколько миноров. Например, в матрице восьмого уровня выделить пять столбцов и пять строк. Брать горизонтальные и вертикальные линии можно произвольно. В местах пересечения будут находиться значения, обозначающие элементы минора пятого порядка.

Записывают их соответственно, начиная с первой строки. После того как все члены выписаны, должен получиться новый определитель пятого порядка. Таких миноров указанного порядка может быть несколько.

В таблице чисел имеется главная диагональ. Начинается она с правого верхнего угла, то есть с элемента a11, и заканчивается на последнем правом элементе. В полученном миноре также можно выделить такую диагональ.

Если взять минор таким способом, что главная его диагональ будет состоять из элементов диагонали исходной таблицы, то такой минор называют главным. Иными словами, эта таблица, которая включает в себя элементы основной диагонали исходной матрицы. При этом необязательно, чтобы в главный минор матрицы были включены все главные элементы. Определитель же, находящийся из первых строк и столбцов, называется угловым минором матрицы.

Базисный определитель показывает, какой наибольший порядок может иметь полученный минор. Например, для системы данных, состоящей из семи строк и восьми столбцов, наибольший определитель может быть седьмого порядка. При этом базисным считается также последний определитель, который не равняется нулю. Если система уравнений имеет девятый порядок и при вычислениях выяснится, что система шестого уровня вырожденная, то предшествующий ему определитель также будет называться базисным. Значение базиса всегда будет наибольшим. Строки и столбцы, из которых состоит базис, называют также базисными. Их может быть несколько.

Когда из исходной таблицы выбран определитель не высшего порядка, то следующий за ним называется окаймляющим. Это значит, что необходимо добавить одну строку и столбец. Такого типа определителей может быть несколько, так как для того, чтобы их построить, можно добавить любую строку или столбец.

Решение задач

Для закрепления материала в школе и высших учебных заведениях учащимся предлагают выполнить расчёт несколько типовых заданий разной сложности. Умение их решать является доказательством понимания теории. Вот некоторые из них рекомендуемые для самостоятельного решения.

Найти в указанной матрице все определители второго уровня и алгебраические дополнения:

Для решения этой задачи нужно рассматривать первую и вторую строчки. Последовательно убирая строки и столбцы методом вычёркивания, можно получить шесть результатов:

В следующей задаче рассматривается квадратная матрица три на три, в которой необходимо найти дополнительную характеристику:

По условию в таблице имеется девять позиций, для которых можно найти дополнительный элемент. При решении нужно последовательно их все перебрать, вычёркивая соответственные столбцы и строки:

В следующем примере необходимо рассчитать первые три алгебраических дополнения. Пусть дана матрица A:

Как видно из примеров, вычисления обычно не вызывают трудностей, но требуют внимательности и усидчивости. Особенно это касается нахождения обратной матрицы. Вычисляется она с помощью алгебраических дополнений, которые равны минорам, умноженным на минус единицу. Довольно часто знаки путают, и в итоге получается неправильный ответ. Поэтому в случае сложных систем есть резон использовать онлайн-калькуляторы.

Использование интернет-калькулятора

В интернете есть определённая группа сайтов, позволяющая выполнять различные математические вычисления в автоматическом режиме. На их страницах содержится специальный скрипт, выполняющий нахождение минора матрицы онлайн любой сложности. При этом от потребителя не требуется никаких особых знаний, он даже и вовсе может ничего не понимать в алгебраических вычислениях.

Всё, что ему необходимо будет сделать для получения ответа, — это ввести исходные данные в предложенную форму и нажать кнопку «Вычислить». Система автоматически определит нужный алгоритм и, используя свойства матрицы, выведет на экран ответ. При этом, кроме результата, пользователю будет предоставлена возможность ознакомиться с подробным решением.

По отзывам потребителей, из множества таких сервисов можно выделить пять следующих сайтов:

Все указанные сайты доступны на русском языке, бесплатны, имеют простой и понятный интерфейс. На их страницах содержится справочная и теоретическая математическая информация. Кроме неё, для каждого раздела приводится типовой пример с объяснением. Использование онлайн-калькуляторов поможет сэкономить время и научит правильно выполнять действия по вычислению миноров.

Их использование будет полезным не только ученикам или студентам, желающим научиться самостоятельно решать задачи, но и инженерам, выполняющим сложные вычисления. Для специалистов они довольно востребованы, так как при самостоятельном решении небольшая ошибка по невнимательности приведёт к неправильному ответу, что исключено при расчёте в автоматическом режиме.

Источник

Нахождение ранга матрицы

В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.

Минор матрицы

Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.

Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.

Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.

Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.

Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.

Другим минором 2-го порядка матрицы А является 0 0 1 1 = 0

Предоставим иллюстрации построения миноров второго порядка матрицы А:

Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:

Иллюстрация, как получается минор 3-го порядка матрицы А:

Для данной матрицы миноров выше 3-го порядка не существует, потому что

Сколько существует миноров k-ого порядка для матрицы А порядка p×n?

Число миноров вычисляют по следующей формуле:

После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.

Ранг матрицы: методы нахождения

Ранг матрицы — наивысший порядок матрицы, отличный от нуля.

Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.

Нахождение ранга матрицы по определению

Метод перебора миноров — метод, основанный на определении ранга матрицы.

Алгоритм действий способом перебора миноров:

Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).

Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.

Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.

Найти ранг матрицы:

Поскольку матрица ненулевая, то ее ранг минимум равен единице.

Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.

Нахождение ранга матрицы методом окаймляющих миноров

Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.

Найти ранг матрицы:

Записываем все окаймляющие миноры:

Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.

Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.

Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.

Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.

Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.

Найти ранг матрицы методом окаймляющих миноров

Поскольку элемент а 11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:

Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)

Вспомним, что представляют собой элементарные преобразования.

путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.

Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).

Справедливость данного утверждения следует из определения матрицы:

в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.

Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.

Проиллюстрируем этот процесс:

1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0

Найти ранг матрицы А при помощи элементарных преобразований:

Поскольку элемент а 11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1 а 11 = 1 2 :

Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3). К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):

Если проводить элементарные преобразования, то не допускаются приближенные значения!

Источник