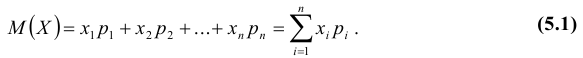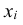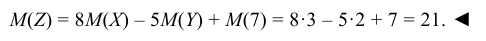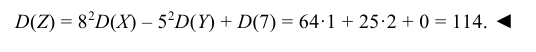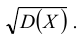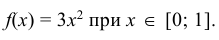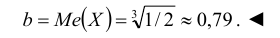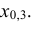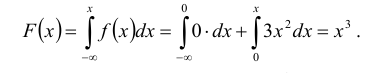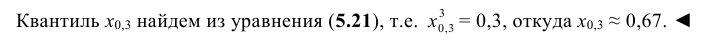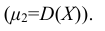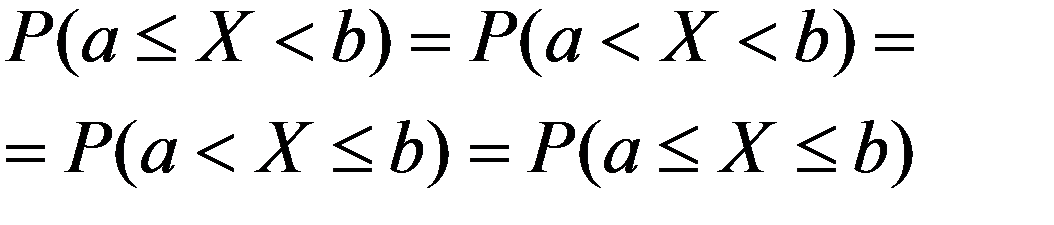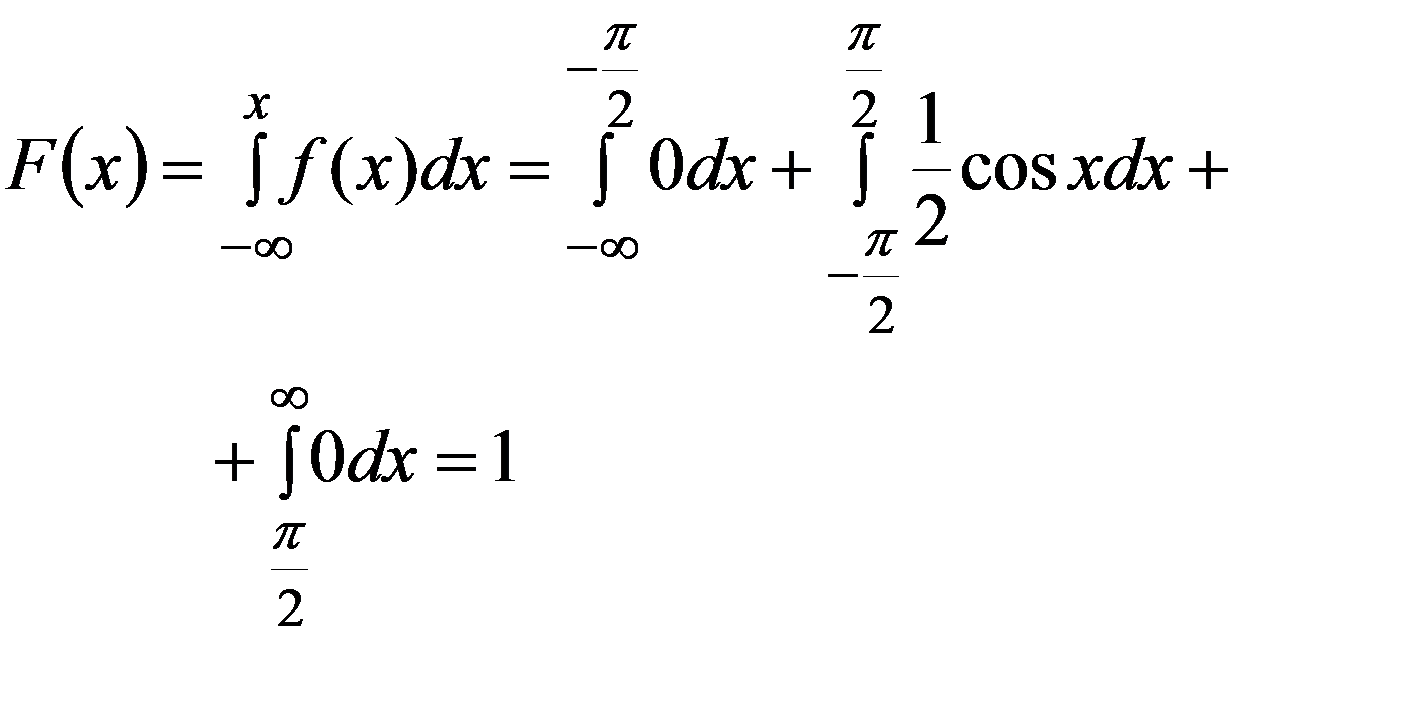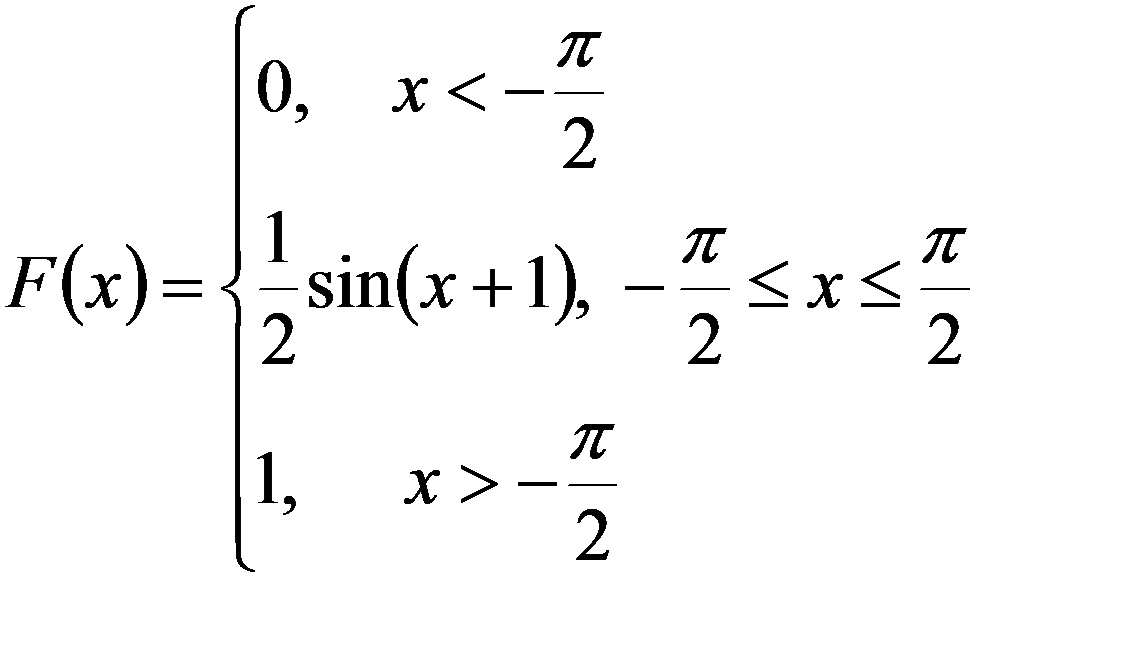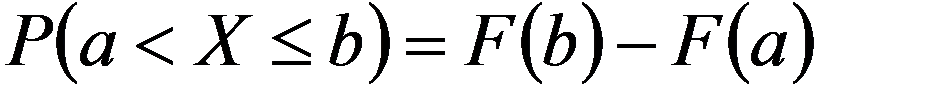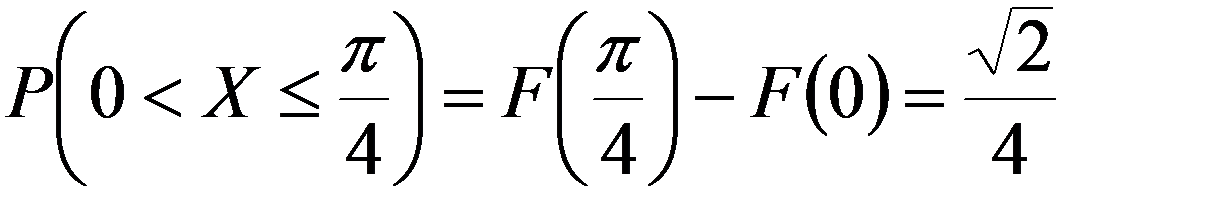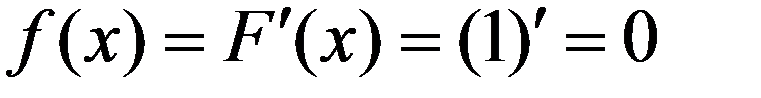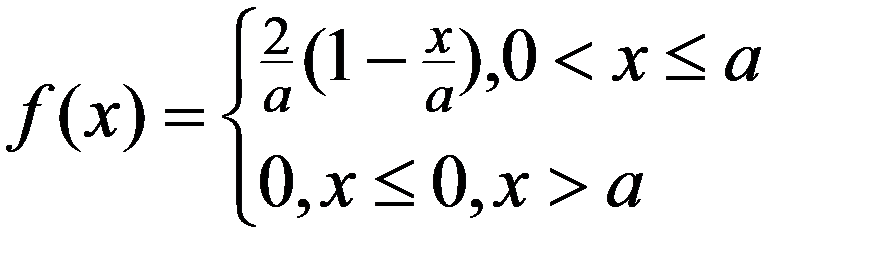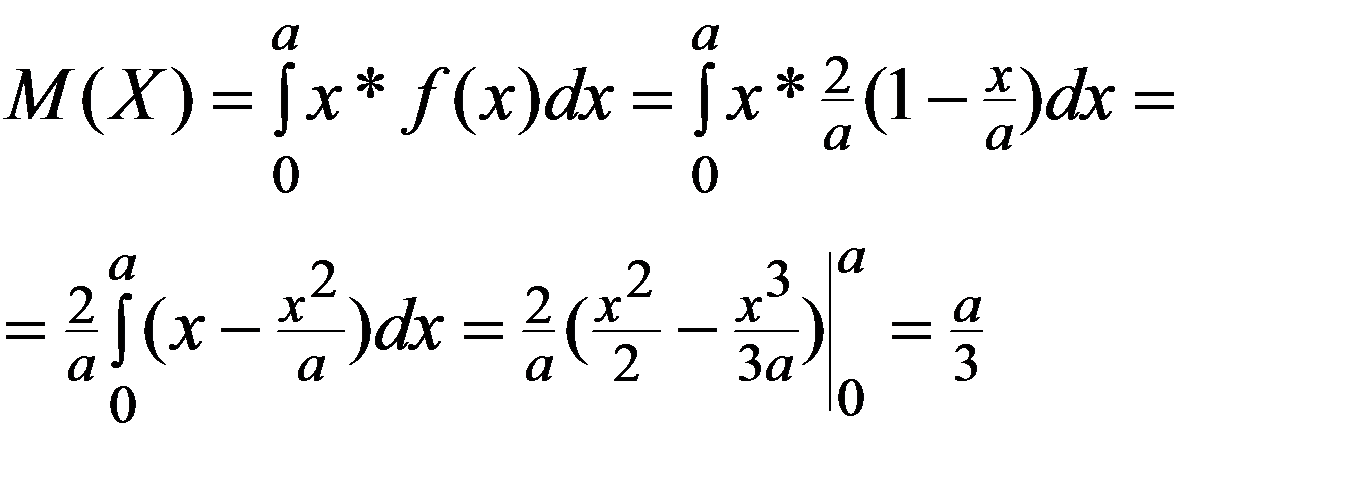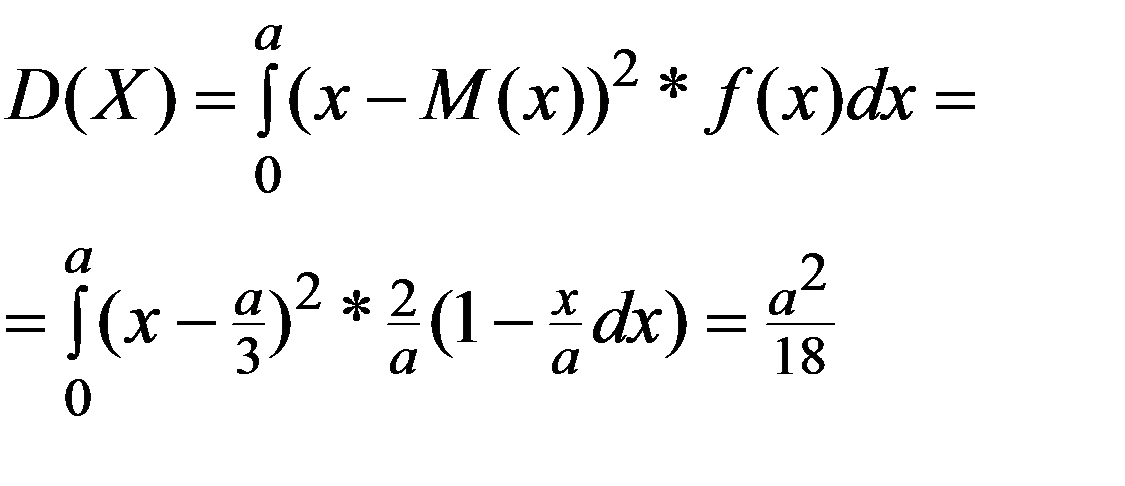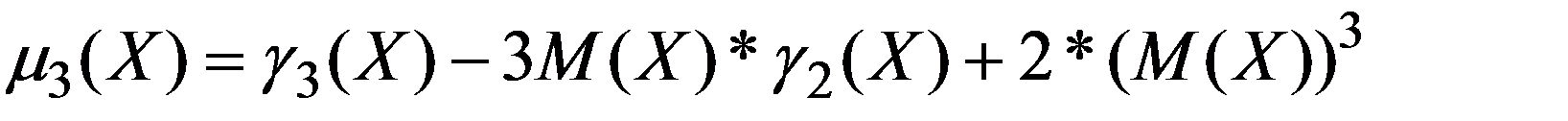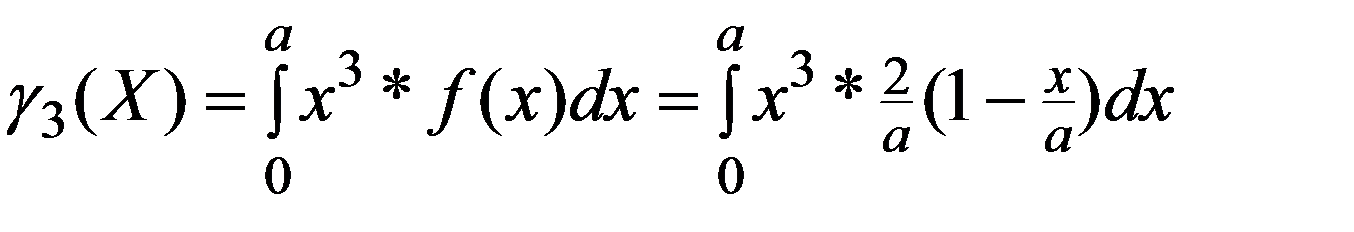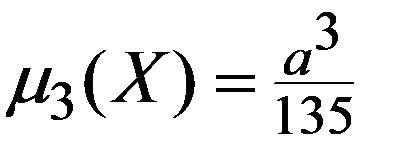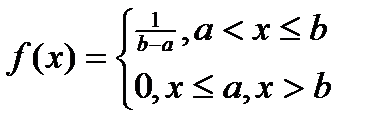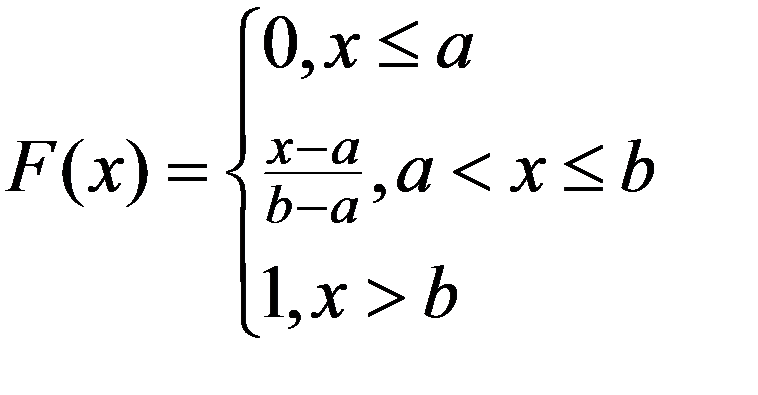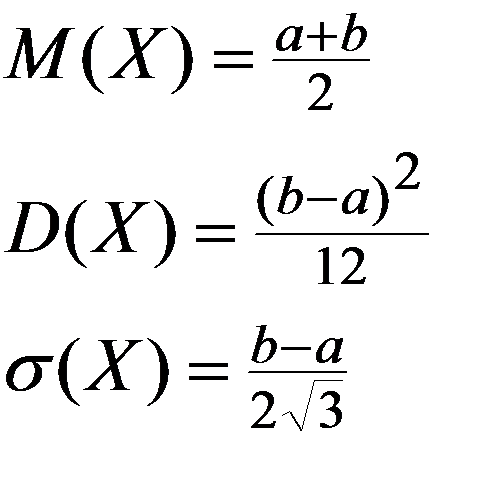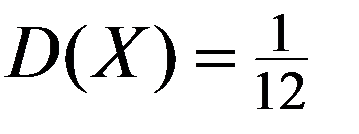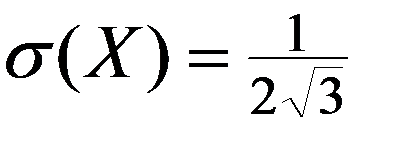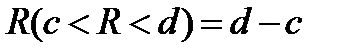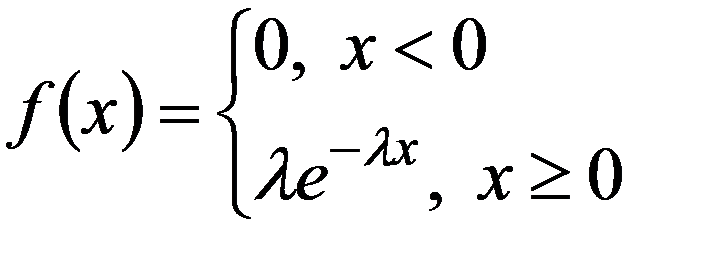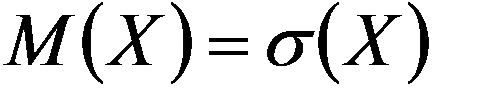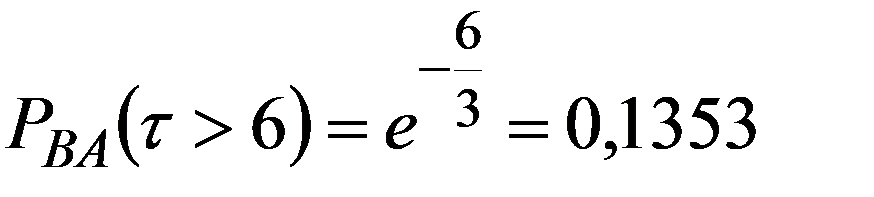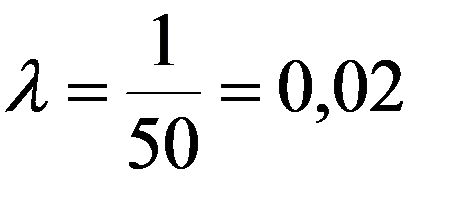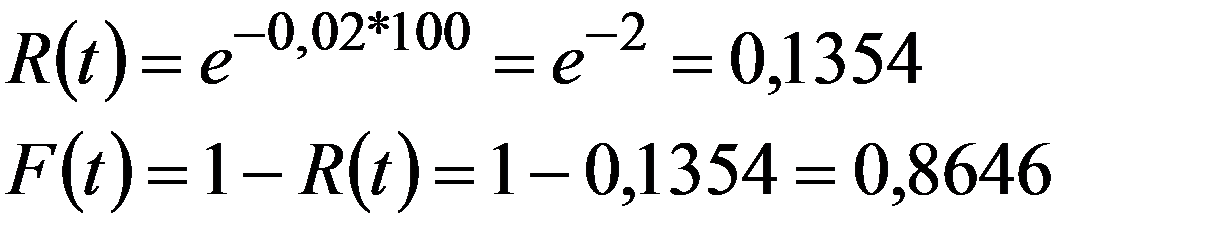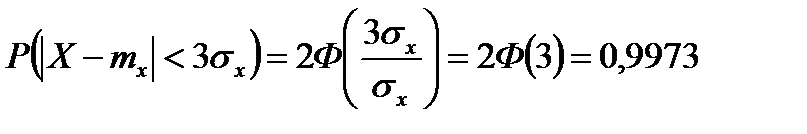Что называется медианой нсв и как ее найти
Содержание:
Числовые характеристики случайных величин:
Как мы уже выяснили, закон распределения полностью характеризует случайную величину, так как позволяет вычислить вероятности любых событий, связанных с этой случайной величиной. Однако, во-первых, закон распределения не всегда известен, а, во-вторых, для решения многих практических задач совсем необязательно знать закон распределения. Достаточно знать отдельные числовые характеристики, которые в сжатой, компактной форме выражают наиболее существенные черты распределения.
Например, можно составить законы распределения двух случайных величин – числа очков, выбиваемых двумя стрелками, – и выяснить, какой из двух стрелков стреляет лучше. Однако, даже не зная законов распределения, можно сказать, что лучше стреляет тот, кто в с р е д н е м выбивает большее количество очков. Таким средним значением случайной величины является математическое ожидание.
Математическое ожидание случайной величины
Определение: Математическим ожиданием, или средним значением, M(X) д и с к р е т н о й случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности: 
Заменим в формуле для дискретной случайной величины знак суммирования по всем ее значениям знаком интеграла с бесконечными пределами, дискретный аргумент xi – непрерывно меняющимся 
Рассмотрим свойства математического ожидания.
Пример:
Найти математическое ожидание случайной величины Z = 8X – – 5Y + 7, если известно, что M(X) = 3, M(Y) = 2.
Решение:
Используя свойства 1, 2, 3 математического ожидания, находим 
Итак, мы установили, что математическое ожидание является важной числовой характеристикой случайной величины. Однако одно лишь математическое ожидание не может в достаточной степени характеризовать случайную величину. Вернемся к задаче о стрелках. При равенстве средних значений числа выбиваемых очков, вопрос о том, какой из стрелков стреляет лучше, остается открытым. Однако в этом случае можно сделать предположение, что лучше стреляет тот стрелок, у которого отклонения числа выбитых очков от среднего значения меньше.
Мерой рассеяния значений случайной величины вокруг ее математического ожидания служит дисперсия (слово дисперсия означает «рассеяние).
Дисперсия случайной величины
Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: 
Для дискретной случайной величины X эта формула принимает вид: 
Для непрерывной случайной величины: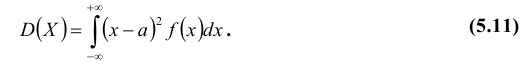 
На практике для вычисления дисперсии часто удобно пользоваться следующей теоремой.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания: 
Для дискретной случайной величины X эта формула принимает вид: 
Для непрерывной случайной величины: 
Рассмотрим свойства дисперсии.
Пример №1
Найти дисперсию случайной величины Z = 8X – 5Y + 7, если известно, что D(X) = 1, D(Y) = 2.
Решение:
Используя свойства дисперсии, находим 
Среднее квадратическое отклонение случайной величины
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют также величину
Определение: Средним квадратическим отклонением (или стандартным отклонением) σ(Х) случайной величины Х называют значение квадратного корня из ее дисперсии: 
Свойства среднего квадратического отклонения вытекают из свойств дисперсии.
Мода и медиана. Квантили
Кроме математического ожидания, дисперсии и среднего квадратического отклонения, в теории вероятностей применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения.
Определение: Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность pi или плотность вероятности f(x) достигает максимума).
Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.
Определение: Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого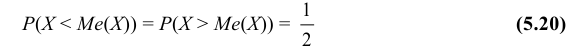 
т. е. вероятность того, что случайная величина Х примет значение, меньшее медианы или большее ее, одна и та же и равна 1/2. Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части. Очевидно, что в точке х = Ме(Х) функция распределения равна 1/2.
Пример №2
Найти моду, медиану случайной величины Х с плотностью вероятности 
Решение:
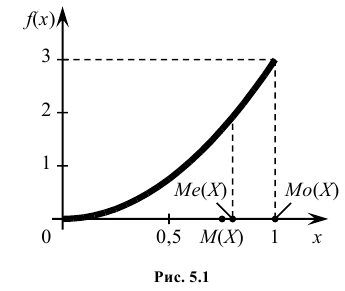
Кривая распределения представлена на рис. 5.1 Очевидно, что плотность вероятности максимальна при х= Мо(Х) = 1. Медиану Ме(Х) = найдем из условия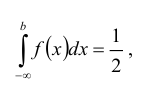 
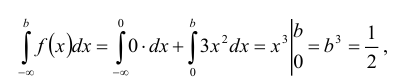
или 
откуда 
Наряду с модой и медианой для описания случайной величины используется понятие квантиля.
Определение: Квантилем уровня q (или q-квантилем) называется такое значение хq случайной величины, при котором функция ее распределения принимает значение, равное q, т. е. 
Пример №3
По данным примера 5.3 найти квантиль 
Решение:
Находим функцию распределения 
Моменты случайных величин. Асимметрия и эксцесс
Среди числовых характеристик случайной величины особое место занимают моменты – начальные и центральные.
Определение: Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени этой величины: 
Для дискретной случайной величины формула начального момента имеет вид: 
Для непрерывной случайной величины: 
Определение: Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k-ой степени отклонения случайной величины Х от ее математического ожидания: 
Для дискретной случайной величины формула центрального момента имеет вид:
Для непрерывной случайной величины: 
Нетрудно заметить, что при k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание
при k = 2 второй центральный момент – дисперсия 
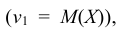
Т.е. первый начальный момент характеризует среднее значение распределения случайной величины Х; второй центральный момент – степень рассеяния распределения Х относительно математического ожидания. Для более подробного описания распределения служат моменты высших порядков.
Третий центральный момент μ3 служит для характеристики ассиметрии (т.е. скошенности ) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на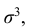 
, где σ – среднее квадратическое отклонение случайной величины Х.
Полученная величина А называется коэффициентом асимметрии случайной величины: 
Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии равен нулю А = 0.
На рис. 5.2 показаны две кривые распределения 1 и 2. Кривая 1 имеет положительную (правостороннюю) асимметрию (А > 0), а кривая 2 – отрицательную (левостороннюю) асимметрию (А
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
19. Числовые характеристики непрерывных случайных величин
Пусть непрерывная случайная величина Х задана функцией распределения F(X). Допустим, что все возможные значения случайной величины принадлежат отрезку [A,B].
Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:
Определение. Средним квадратичным отклонением Называется квадратный корень из дисперсии.
Определение. Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется Двухмодальным или Многомодальным.
Если распределение имеет минимум, но не имеет максимума, то оно называется Антимодальным.
Определение. Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.
Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.
Определение. Начальным моментом Порядка K Случайной величины Х называется математическое ожидание величины ХK.
Для дискретной случайной величины: 
.
Для непрерывной случайной величины: 
.
Начальный момент первого порядка равен математическому ожиданию.
Определение. Центральным моментом Порядка K случайной величины Х называется математическое ожидание величины 
Для дискретной случайной величины: 
.
Для непрерывной случайной величины: 
.
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется Коэффициентом асимметрии.
Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая Эксцессом.
Кроме рассмотренных величин используются также так называемые абсолютные моменты:
Абсолютный начальный момент: 
.
Абсолютный централь Ный момент: 
.
Абсолютный центральный момент первого порядка называется Средним арифметическим отклонением.
Пример. Для рассмоТРенного выше примера определить математическое ожидание и дисперсию случайной величины Х.
Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.
Т. к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).
Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна 
Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз.
Для составления закона распределения надо найти вероятности каждого из этих событий.
1) Белый шар не появился вовсе: 
2) Белый шар появился один раз: 
3) Белый шар появиться два раза: 
.
4) Белый шар появиться три раза: 
5) Белый шар появиться четыре раза: 
6) Белый шар появился пять раз: 
Получаем следующий закон распределения случайной величины Х.
IV. Медиана
III. Среднеквадратическое отклонение
II. Дисперсия
I. Математическое ожидание
ЧИСЛОВЫЕХАРАКТЕРИСТИКИ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Числовыми характеристиками непрерывной случайной величины, как и дискретной, являются математическое ожидание, дисперсия и среднеквадратическое отклонение.
Математическое ожидание указывает, какое среднеезначение случайной величины следует ожидать в результате проведения испытания. Математическим ожиданием дискретной случайной величины мы назвали сумму произведений всех возможных значений случайной величины (хi) на соответствующие вероятности (рi): M(X) = х1·р1 + х2·р2+…+ хn·рn.
Что же изменится в случае непрерывной случайной величины? Запишем M(X) для ДСВ по-другому, используя значок суммы: M(X) = .
Теперь воспользуемся уже знакомыми нам аналогиями:
Тогдаматематическим ожиданием НСВ называют число где f(x) – функция плотности вероятности.
Так же, как и для ДСВ, математическое ожидание НСВ характеризует среднее значение.
Найдем математическое ожидание в примере 24.1.
следовательно (т.к. при f(x) = 0 крайние интегралы равны нулю: ),
Дисперсия НСВ, как и ДСВ, характеризует степень отклонения значений случайной величины от ее среднего значения.
Дисперсией случайной величины Х называют математическое ожидание квадрата ее отклонений от среднего значения. Это определение сохраняется и для НСВ, как и формула для вычисления дисперсии:
Меняется лишь правило нахождения M(X 2 ).
Найдем дисперсию в примере 24.1.
Дисперсия имеет размерность квадрата случайной величины. Для того, чтобы оценка рассеяния значений случайной величины имела размерность самой величины, вычисляют среднеквадратическое отклонение.
Положительное значение квадратного корня из дисперсии называется среднеквадратическим отклонением (или стандартным отклонением) как для ДСВ, так и для НСВ:
Так в примере 24.1.среднеквадратическое отклонение
Рассмотрим еще одну важную числовую характеристику НСВ – медиану.
Медианой непрерывной случайной величины Х называется такое ее значение Ме, что P<X Me>. Это означает, что вероятность осуществления события до Me равна вероятности осуществления события после Me, и, следовательно, равна ½ (сумма вероятностей для всех значений случайной величины всегда равна 1).
Если на чертеже провести прямую х=Me, она разделит площадь под кривой у= f(x) на две равные части.
| S2 |
| S1 |
| 2 |
| 1 |
| 0,7 |
| у=f(х) |
| х |
| S1= S2 |
Контрольные вопросы:
1. Обоснуйте необходимовть нахождения числовых характеристик случайной величины.
2. Что называют математическим ожиданием НСВ? В каких единицах оно измеряется? Что оно характеризует?
3. Что называют дисперсией НСВ? В каких единицах она измеряется? Что она характеризует? Может ли дисперсия быть отрицательной?
4. Что называют среднеквадратическим отклонением НСВ? В каких единицах оно измеряется? Что оно характеризует?
5. Что называют медианой НСВ? В каких единицах она измеряется? Какова формула для расчёта медианы? Как изабразить медиану на графиках у= f(x) и у= F(x)?
6. Решите задачу: Интегральная функция распределения задана выражением:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Формы представления закона распределения НСВ.
Ряд распределения, многоугольник распределения и формула не используются в качестве закона распределения НСВ.
 |
 |
 |
 |
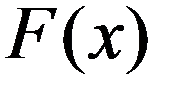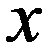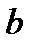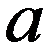Из свойства 2 функции распределения вытекает важное следствие для НСВ: вероятность того, что НСВ примет одно определенное значение равна 0. И тогда
Таким образом, не представляет интереса говорить о вероятности того, что НСВ примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малой.
(3.7)
(3.8)
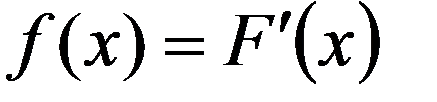
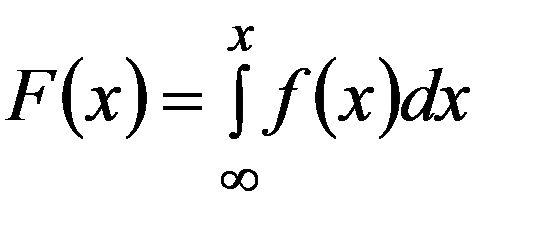
Геометрически F(x) есть площадь кривой распределения, лежащая левее точки x.
График f(x) называется кривой распределения.
Размерность f(x) обратна размерности СВ (это не вероятность).
1. f(x) неотрицательная функция, т.е. f(x) ≥ 0
2.Несобственный интеграл от f(x) на интервале (-∞; +∞) равен 1.
(3.9)
Это так называемое условие нормировки плотности распределения.
(3.10)
(3.11)
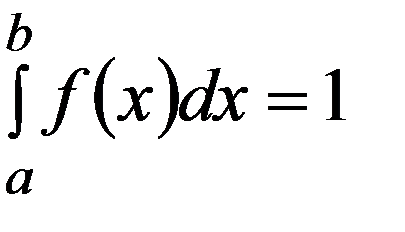
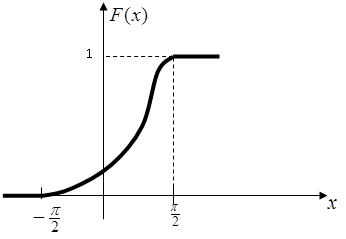
Геометрически это означает, что P (a π/2 
4.Согласно второму свойству F(x) 
Числовые характеристики НСВ.
(3.12)
(3.13)
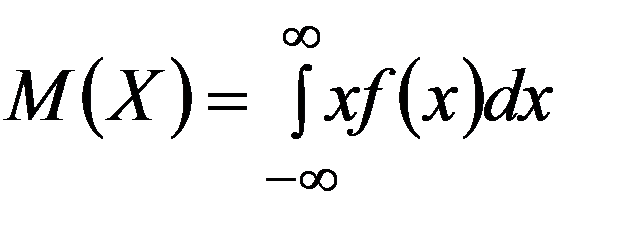
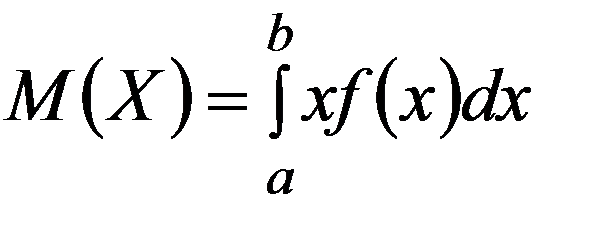
Медиана НСВ X геометрически – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
Дисперсия НСВ X
(3.14)
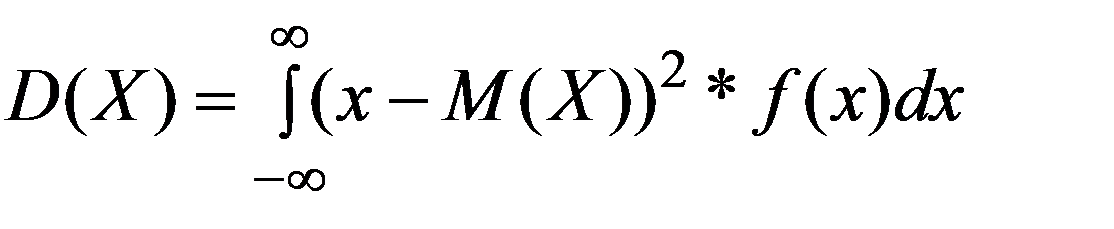
или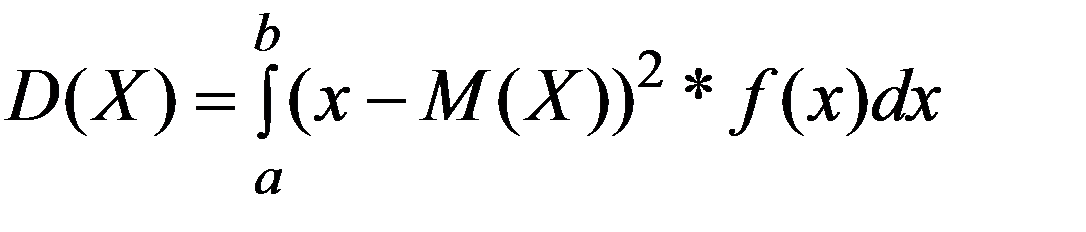 
(3.15)
СКО НСВ X
(3.16)
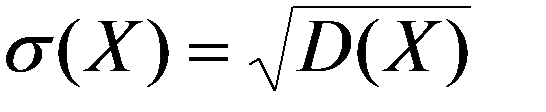
Начальный теоретический момент k-го порядка НСВ X :
(3.17)
(3.18)
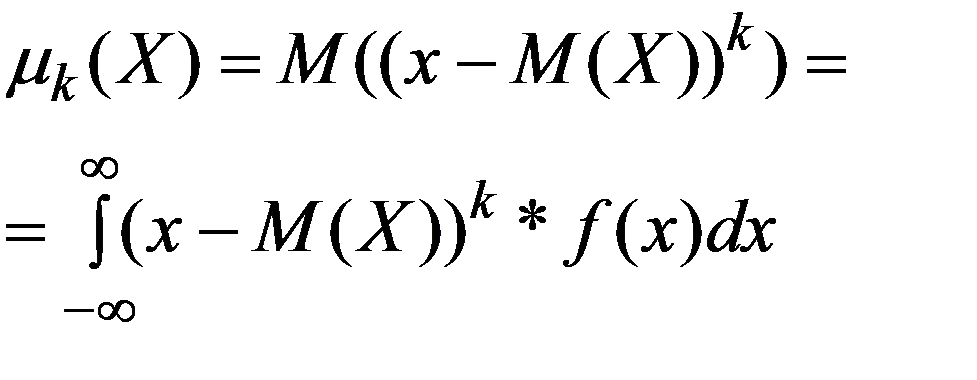
Найти числовые характеристики M(X), D(X), σ (X), µ3 (X)
1.По (3.7) определим f(x)
при x ≤ 0, 
при 0 a, 
2. По (3.13) 
3. По (3.15) 
4. По (3.16) 
5. 
Основные (типовые) законы распределения НСВ.
График f(x) имеет вид:
 |
 |
 |
 |
 |
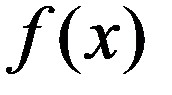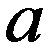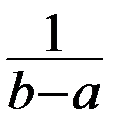Функция распределения F(x) 
Числовые характеристики: 
Частный случай равномерного закона распределения НСВ – НСВ R равномерно распределенная на интервале (0,1), для которой
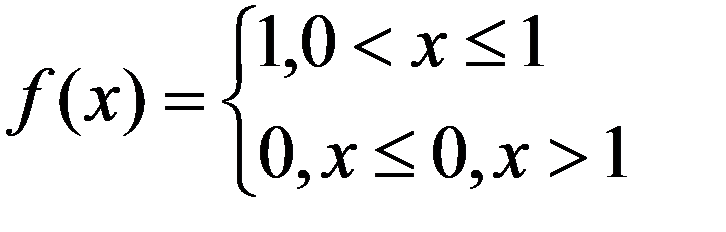
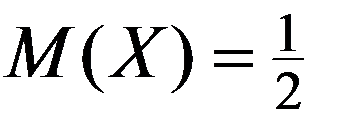
Значения НСВ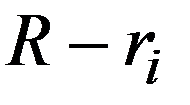 
называются случайными числами.
Вероятность попадания НСВ R в результате испытания в интервал (c,d) равна его длине 
НСВ имеет показательное (экспотенциальное) распределение, если её плотность выражается формулой:
График f(x) имеет вид
 |
 |
 |
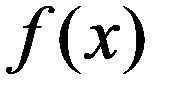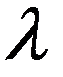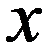Функция распределения F(x)
Числовые характеристики:
, 
, 
, 
(3.19)
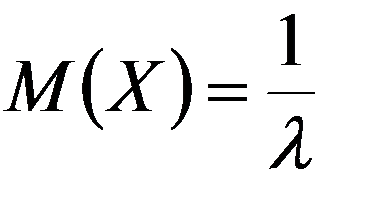
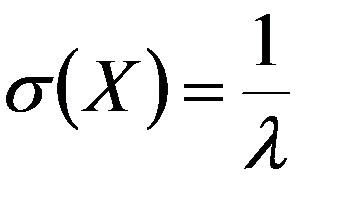
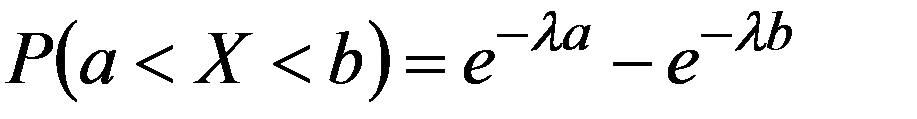
1. По соединительной линии между пунктами A и B осуществляются телефонные разговоры со средней длительностью 4 мин. для направления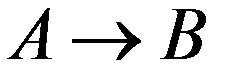 
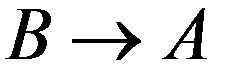
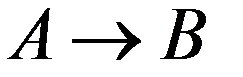
и 3 мин. для 
. Вызовы 
составляют 55% всех вызовов. Найти вероятность того, что некоторый разговор длятся дольше 6 минут.
(3.20),
а вероятность того, что разговор не закончится до момента t :
(3.21)
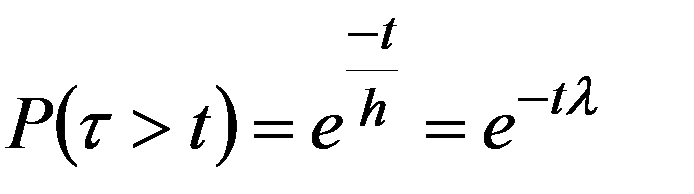
По формуле полной вероятности (2.20)
Пример 2.Элемент отказывает в среднем 1 раз за 50 часов непрерывной работы. Считая, что время безотказной работы распределено по показательному закону, найти вероятность отказа за 100 часов.
Тогда интегральная функция
(3.22)
(3.23)
(3.24)
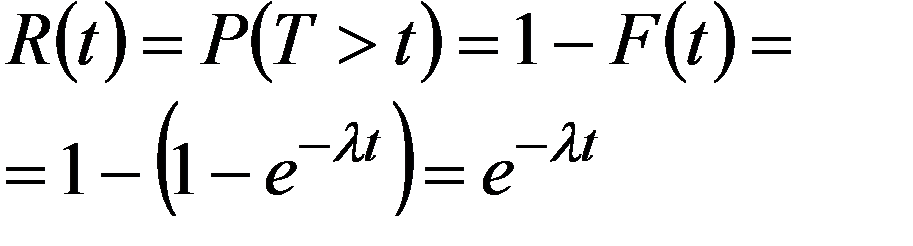
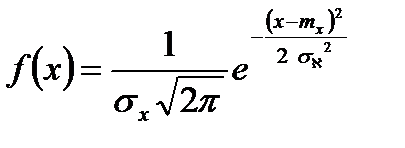
или нормированное распределение с параметрами mx = 0 и σx = 1, если её плотность
(3.25)
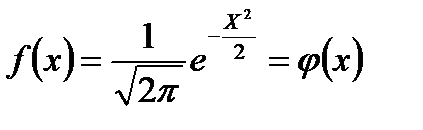
График плотности нормального распределения называют нормальной кривой (кривой Гаусса)
 |
 |
 |
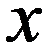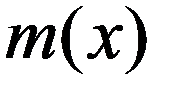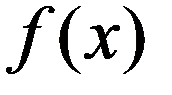1. Определена на всей оси x
2. Принимает только положительные значения.
3. Ось 0x является горизонтальной асимптотой графика f(x).
4. Имеет только один максимум в точке mx.
6. Точки на кривой с координатами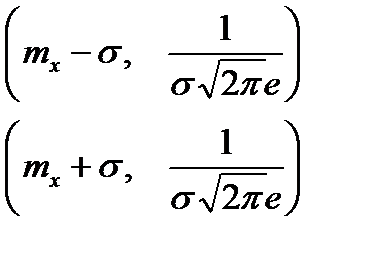 
являются точками перегиба.
При изменении mx форма нормальной кривой не изменяется, она сдвигается вдоль оси 0x вправо, если mx возрастает, и влево, если mx уменьшается.
Интегральная функция F(x) общего нормального распределения
(3.26)
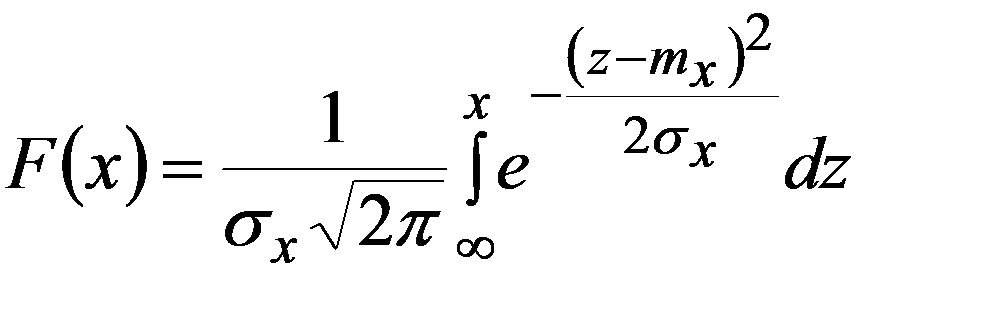
а нормированного распределения
(3.27)
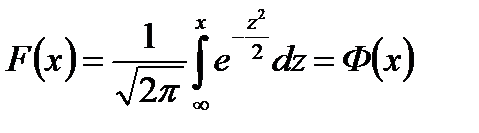
есть функция Лапласа Ф(х)
(3.28)
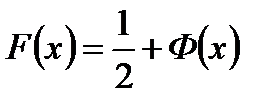
Нормальное распределение зависит от двух параметров mx и σx.
Вероятность попадания НСВ X в интервал (a,b)
(3.29)
, где 
— половина длины участка.
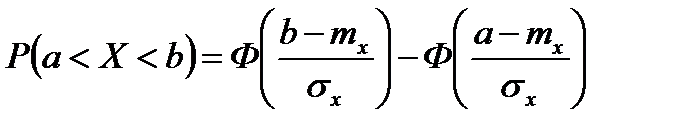
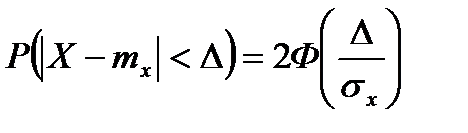
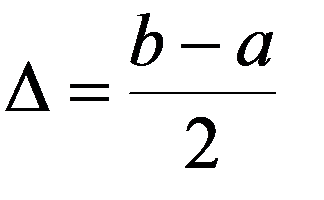
1.Проверить правило 3-х сигм
т.е. возможные значения нормальной НСВ X попадут в интервал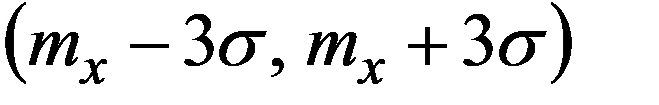 
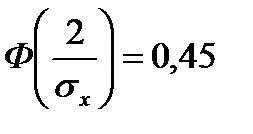
с вероятностью P=0,9973.
Нормальный закон является наиболее важным, как в теории, так и на практике, т.к. большинство наблюдаемых явлений подчиняются этому закону и он считается предельным законом, к которому приближаются другие законы распределения при определенных часто встречающихся типичных условиях.
Система двух СВ (двумерная СВ)
Система двух СВ может быть полностью представлена законом распределения, частично – числовыми характеристиками.
Законом распределения вероятностей двумерной СВ называют соответствие между возможными значениями СВ и их вероятностями.
Закон распределения двумерной СВ может быть задан
2) интегральной функцией распределения;
3) дифференциальной функцией распределения (двумерной плотностью распределения).
Для дискретных двумерных СВ закон распределения имеет вид 1 или 2, для непрерывных – 2 или 3. Функция распределения – универсальный способ представления закона распределения системы двух СВ.
Дата добавления: 2015-12-26 ; просмотров: 2364 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ