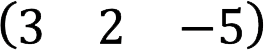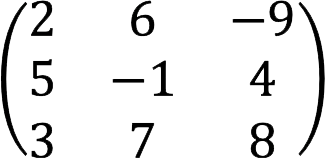Что называется матрицей строкой матрицей столбцом вектором
Что называется матрицей строкой матрицей столбцом вектором
Матрицей 
размерности m×n называется таблица чисел aij, содержащая m строк и n столбцов. Числа aij называются элементами этой матрицы, где i – номер строки, j – номер столбца, на пересечении которых стоит данный элемент. Матрица, содержащая m строк и n столбцов, имеет вид:
Виды матриц:
1) при m=n – квадратная, в данном случае n называют порядком матрицы;
2) квадратная матрица, у которой все недиагональные элементы равны нулю – диагональная;
3) диагональная матрица, у которой все диагональные элементы равны единице – единичная и обозначается E;
4) при n≠m – прямоугольная;
5) при m=1 – матрица-строка (вектор-строка);
6) при n=1 – матрица-столбец (вектор-столбец);
7) при всех aij =0 – нулевая матрица.
Заметим, что основной числовой характеристикой квадратной матрицы является ее определитель. Определитель, соответствующий матрице n-го по-порядка, также имеет n-ый порядок.
Дадим ряд необходимых определений.
Определителем матрицы 2-го порядка называется число
Минором Мij элемента aij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, полученной из матрицы А путем вычеркивания i-ой строки и j-го столбца.
1. При транспонировании матрицы ее определитель не меняется.
2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак.
3. Определитель, имеющий две пропорциональные (равные) строки (столбца), равен нулю.
4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
5. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), предварительно умноженные на любое число.
7. Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.
Поясним данное свойство на примере определителя 3-го порядка. В данном случае свойство 7 означает, что
Свойство 7 представляет собой теорему о разложении определителя, сформулированную Лапласом.
8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.
Последнее свойство часто называют псевдоразложением определителя.
Виды матриц
Виды матриц не по зубам? Тебе ответит эксперт через 10 минут!
Диагональные матрицы
Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.
Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.
Треугольные матрицы
Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.
Ступенчатая матрица
Ступенчатой называется матрица, удовлетворяющая следующим условиям:
Другое определение ступенчатой матрицы.
$$A=\left(\begin
Другое определение ступенчатой матрицы.
Примеры ступенчатых матриц:
Примеры матриц, которые не являются ступенчатыми:
Решение. Проверяем выполнение условий из определения:
Виды матриц с примерами
В данной публикации мы рассмотрим, какие виды матриц существуют, сопроводив их практическими примерами для демонстрации изложенного теоретического материала.
Напомним, что матрица – это некая прямоугольная таблица, состоящая из столбцов и строк, которые заполнены определенными элементами.
Виды матриц
1. Если матрица состоит из одной строки, она называется вектор-строкой (или матрицей-строкой).
2. Матрица, состоящая из одного столбца, называется вектором-столбцом (или матрицей-столбцом).
4. Нулевая – матрица, все элементы которой равняются нулю ( aij = 0).
5. Диагональная – квадратная матрица, у которой все элементы, за исключением расположенных на главной диагонали, равняются нулю. Одновременно является верхней и нижней треугольной.
6. Единичная – это разновидность диагональной матрицы, у которой все элементы главной диагонали равны единице. Обычно обозначается буквой E.
7. Верхняя треугольная – все элементы матрицы ниже главной диагонали равны нулю.
8. Нижняя треугольная – матрица, все элементы которой выше главной диагонали равняются нулю.
9. Ступенчатая – матрица, для которой выполняются следующие условия:
Матрица (математика)
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.
Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n; и обратно — каждой квадратной матрице порядка n может быть сопоставлен единственный линейный оператор, действующий в этом пространстве. [2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.
То же можно сказать о представлении матрицами билинейный (квадратичных) форм.
В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
Содержание
История
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Также волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г. [3]
Определение
Пусть есть два конечных множества 
и 
, где 
и 
— натуральные числа.
Назовём матрицей размера 
(читается на ) с элементами из некоторого кольца или поля 
отображение вида
.
называется элементом матрицы, находящимся на пересечении 
-той строки и 
-ого столбца;
Если индекс пробегает множество 
, а пробегает множество 
, то совокупность элементов полностью определяет матрицу.
Таким образом, матрица размера состоит в точности из
В соответствии с этим
Сама матрица естественным образом интерпретируется как вектор в пространстве 
, имеющем размерность 
. Это позволяет ввести покомпонентное сложение матриц и умножение матрицы на число (см. ниже); что касается матричного умножения, то оно существенным образом опирается на прямоугольную структуру матрицы.
Если у матрицы количество строк совпадает с количеством столбцов , то такая матрица называется квадратной, а число 
называется размером квадратной матрицы или её порядком.
Обозначения
Обычно матрицу обозначают заглавной буквой латинского алфавита: пусть
,
тогда 
— матрица, которая интерпретируется как прямоугольный массив элементов поля вида 
, где
таким образом, 
— элемент матрицы , находящийся на пересечении -той строки и -того столбца. В соответствии с этим принято следующее компактное обозначение для матрицы размера :
если нужно просто указать обозначение для элементов матрицы.
Иногда, вместо , пишут 
, чтобы отделить индексы друг от друга и избежать смешения с произведением двух чисел.
Если необходимо дать развёрнутое представление матрицы в виде таблицы, то используют запись вида
Можно встретить как обозначения с круглыми скобками «(…)», так и обозначения с квадратными скобками «[…]». Реже можно встретить обозначения с двойными прямыми линиями «||…||»).
Поскольку матрица состоит из строк и столбцов, для них используются следующие обозначения:
— это -тая строка матрицы ,
— это -тый столбец матрицы .
Таким образом, матрица обладает двойственным представлением — по строкам:
.
Такое представление позволяет формулировать свойства матриц в терминах строк или в терминах столбцов.
Транспонированная матрица
С каждой матрицей 
размера связана матрица 
размера 
вида
Такая матрица называется транспонированной матрицей для и обозначается так 
.
Транспонированную матрицу можно получить, поменяв строки и столбцы матрицы местами. Матрица размера при этом преобразовании станет матрицей размерностью .
Диагональная матрица
Диагональная матрица — квадратная матрица, все элементы которой кроме диагональных — нулевые 
, иногда записывается как:
Единичная матрица
Единичная матрица — матрица, при умножении на которую любая матрица (или вектор) остается неизменной, является диагональной матрицей с единичными (всеми) диагональными элементами:
Для ее обозначения чаще всего используется обозначение I или E, а также просто 1 (или 1 специальным шрифтом).
Для обозначения ее элементов также используется символ Кронекера 
, определяемый как:
при 
Нулевая матрица
Для обозначения нулевой матрицы — матрицы, все элементы которой нули (при сложении ее с любой матрицей та остается неизменной, а при умножении на любую получается нулевая матрица) — используется обычно просто 0 или 0 специальным шрифтом, или буква, начертанием похожая на ноль, например 
.
Вектор-строка и вектор-столбец
Матрицы размера 
и 
являются элементами пространств 
и 
соответственно:
Операции над матрицами
Умножение матрицы на число
Умножение матрицы на число 
(обозначение: 
) заключается в построении матрицы 
, элементы которой получены путём умножения каждого элемента матрицы на это число, то есть каждый элемент матрицы равен
Свойства умножения матриц на число:
Сложение матриц
Сложение матриц 
есть операция нахождения матрицы 
, все элементы которой равны попарной сумме всех соответствующих элементов матриц и , то есть каждый элемент матрицы равен
Свойства сложения матриц:
Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:
Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образуют линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.
Умножение матриц
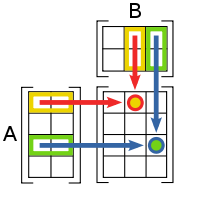
Умножение матриц (обозначение: 
, реже со знаком умножения 
) — есть операция вычисления матрицы , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
Количество столбцов в матрице должно совпадать с количеством строк в матрице , иными словами, матрица обязана быть согласованной с матрицей . Если матрица имеет размерность , — 
, то размерность их произведения 
есть 
.
Свойства умножения матриц:
Умножение вектора на матрицу
По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:
для вектора-столбца v (получая новый вектор-столбец Av):
для вектора-строки s (получая новый вектор-строку sA):
Вектор-строка, матрица и вектор столбец могут быть умножены друг на друга, давая число (скаляр):
(Порядок важен: вектор-строка слева, вектор-столбец справа от матрицы).
Эти операции являются основой матричного представления линейных операторов и линейных преобразований координат (смены базисов), таких, как повороты, масштабирования, зеркальные отражения, а также (последнее) матричного представления билинейных (квадратичных форм.
Заметим, что обычной мотивировкой введения матриц и определения операции матричного умножения (см.тж.в статье об умножении матриц) является именно введение их, начиная с умножения вектора на матрицу (которое вводится исходя из преобразований базиса или вообще линейных операций над векторами), а уже затем композиции преобразований сопоставляется произведение матриц. Действительно, если новый вектор Av, полученный из исходного вектора v преобразованием, представимым умножением на матрицу A, преобразовать теперь еще раз, преобразованием, представимым умножением на матрицу B, получив B(Av), то, исходя из правила умножения вектора на матрицу, приведенного в начале этого параграфа (используя ассоциативность умножения чисел и меняя порядок суммирования), нетрудно увидеть в результате формулу, дающую элементы матрицы (BA), представляющую композицию первого и второго преобразований, и совпадающую с обычным определением матричного умножения.
Комплексное сопряжение
Если элементами матрицы являются комплексные числа, то комплексно сопряжённая (не путать с эрмитово сопряжённой! см. далее) матрица равна 
. Здесь 
— число, комплексно сопряжённое к 
.
Транспонирование и эрмитово сопряжение
Транспонирование уже обсуждалось выше: если , то 
. Для комплексных матриц более употребительно эрмитово сопряжение: 
. С точки зрения операторного взгляда на матрицы, транспонированная и эрмитово сопряжённая матрица — это матрицы оператора, сопряжённого относительно скалярного или эрмитова произведения, соответственно.
Для квадратной матрицы определен след:
(иногда также обозначается как Sp или Spur).
Является инвариантом ортогональных (унитарных) преобразований матрицы, соответствующих преобразованию матричного представления линейного оператора или билинейной (квадратичной) формы при соотвестствующем преобразовании векторного пространства (например, вращении).