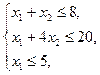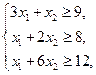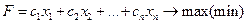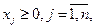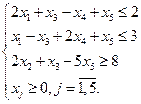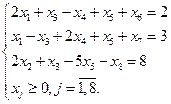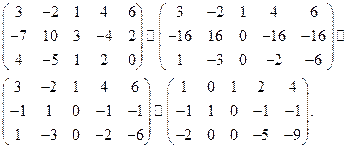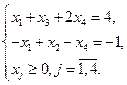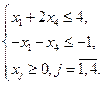Что называется математической моделью экономической задачи и как она строится
Математическая модель задачи линейного программирования



Т10. Постановка задачи линейного программирования
Математической моделью экономической задачи называется совокупность математических соотношений, описывающих экономический процесс.
Для составления математической модели необходимо:
1. выбрать переменные задачи;
2. составить систему ограничений;
3. задать целевую функцию.
Переменными задачи называются величины х1, х2,…, хn, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора Х = (х1, х2,…, хn).
Системой ограничений задачи называется совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов и других экономических условий, например, положительности переменных. В общем случае они имеют вид:
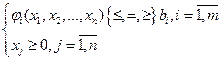
Целевой функцией называется функция F(X) = f(х1, х2,…, хn) переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти переменные задачи х1, х2,…, хn, которые обеспечивают экстремум целевой функции
и удовлетворяют системе ограничений (1).
Если целевая функция (2) и система ограничений (1) линейны, то задача математического программирования называется задачей линейного программирования (ЗЛП).
Вектор Х (набор переменных задачи) называется допустимым решением, или планом ЗЛП, если он удовлетворяет системе ограничений (1). Допустимый план Х, который обеспечивает экстремум целевой функции, называется оптимальным решением ЗЛП.
2. Примеры составления математических моделей экономических задач
К ЗЛП приводит исследование конкретных производственных ситуаций, которые интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
1.Задача об оптимальном производственном плане
Для производства двух типов изделий Т1 и Т2 используются три вида ресурсов S1, S2, S3. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, а также прибыль от реализации единицы продукции приведены в таблице:
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции |
| Т1 | Т2 | |
| S1 S2 S3 | — | |
| Прибыль, ден.ед. |
Требуется найти такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Обозначим х1, х2 – число единиц продукции соответственно Т1 и Т2, запланированных к производству. Для их изготовления потребуется (х1 + х2) единиц ресурса S1, (х1 + 4х2) единиц ресурса S2, (х1) единиц ресурса S3. Потребление ресурсов S1, S2, S3 не должно превышать их запасов, соответственно 8, 20 и 5 единиц.
Тогда экономико-математическую модель задачи можно сформулировать так:
Найти план выпуска продукции Х = (х1, х2), удовлетворяющий системе ограничений:
и условию 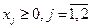
при котором функция 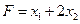
Задачу можно легко обобщить на случай выпуска n типов продукции с использованием m видов ресурсов.
2.Задача об оптимальном рационе
Имеется два вида корма К1 и К2, содержащие питательные вещества S1, S2 и S3. Содержание числа единиц питательных веществ в 1кг каждого вида корма, необходимый минимум питательных веществ, а также стоимость 1кг корма приведены в таблице:
| Питательное вещество | Необходимый минимум питательных веществ | Число единиц питательных веществ в 1кг корма |
| К1 | К2 | |
| S1 S2 S3 | ||
| Cтоимость 1кг корма, ден.ед. |
Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.
Обозначим х1, х2 – количество кормов К1 и К2, входящих в дневной рацион. Тогда этот рацион будет включать (3х1 + х2) единиц питательного вещества S1, (х1 +2х2) единиц вещества S2, (х1+6х2) единиц питательно вещества S3. Так как содержание питательных веществ S1, S2 и S3 в рационе должно быть соответственно 9, 8 и 12 единиц, то экономико-математическую модель задачи можно сформулировать так:
Составить дневной рацион Х = (х1, х2), удовлетворяющий системе ограничений:
и условию 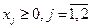
при котором функция 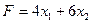
Формы записи ЗЛП
В ЗЛП требуется найти экстремум линейной целевой функции:
и условии неотрицательности
где аij, bi, cj ( 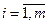

Так записывается ЗЛП в общей форме. Если система ограничений содержит только неравенства, то ЗЛП представлена в стандартной форме. Канонической (основной) формой записи ЗЛП называется запись, когда система ограничений содержит только равенства. Так что приведенные выше ЗЛП записаны в стандартной форме.
Общая, стандартная и каноническая формы ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в другой форме. Это значит, что если есть способ решения одной из указанных задач, то может быть определен оптимальный план любой из задач.
Чтобы перейти от одной формы записи ЗЛП к другой надо уметь переходить от ограничений-неравенств к ограничениям-равенствам и наоборот.
Ограничение – неравенство (£) можно преобразовать к ограничению-равенству добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство (³) – в ограничение равенство вычитанием из его левой части дополнительной неотрицательной переменной. Число вводимых дополнительных неотрицательных переменных равно числу преобразуемых ограничений-неравенств.
Вводимые дополнительные переменные имеют определенный экономический смысл. Так, если в ограничениях исходной ЗЛП отражаются расход и наличие ресурсов, то значение дополнительной переменной ЗЛП в канонической форме равно объему неиспользуемого соответствующего ресурса.
Пример 1. Записать в канонической форме ЗЛП:
Найти
Целевая функция остается без изменений:
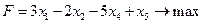
Система неравенств преобразуется в систему равенств:
При решении ЗЛП графическим методом требуется переход от канонической формы к стандартной форме.
Для приведения ЗЛП к стандартной форме используется метод Жордана – Гаусса решения СЛАУ. В отличие от метода Гаусса, в котором расширенная матрица системы приводится к ступенчатому виду, в методе Жордана – Гаусса в составе расширенной матрицы формируется единичная матрица. Поэтому обратный ход здесь не требуется.
Для преобразования исходной канонической ЗЛП в эквивалентную стандартную ЗЛП:
б) разрешающая строка переписывается без изменения, а все элементы разрешающего столбца, кроме разрешающего, заменяются нулями. Остальные элементы расширенной матрицы определяются с помощью «правила прямоугольника»:
Рассмотрим четыре элемента расширенной матрицы: элемент аij, подлежащий преобразованию, разрешающий элемент aqp и элементы аiр и aqj. Для нахождения элемента аij следует из элемента аij вычесть произведение элементов аiр и aqj, расположенных в противоположных вершинах прямоугольника, деленное на разрешающий элемент aqp:
в) одновременно исключаются разрешенные неизвестные из целевой функции. Для этого в расширенной матрице в последней строке записываются коэффициенты целевой функции. При вычислениях учитывается, что разрешающий элемент в последней строке выбирать нельзя.
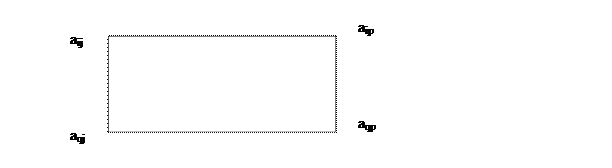
Пример 2. Привести к стандартному виду:
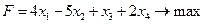
Методом Жордана – Гаусса приведем систему уравнений-ограничений ЗЛП к равносильной системе неравенств. Выберем в качестве разрешающего элемента третий элемент первой строки:
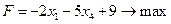
Т.к. переменные х2 и х3 неотрицательные, то отбросив их, можно записать ЗЛП в симметричном виде:
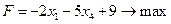
Свойства ЗЛП
1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.
Множество точек называется выпуклым, если оно содержит весь отрезок, соединяющий две любые точки этого множества.
Согласно этому определению многоугольник на рис.1а является выпуклым множеством, а многоугольник на рис.1б таковым не является, т.к. отрезок MN между двумя его точками M и N не полностью принадлежит этому многоугольнику.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются круг, сектор, отрезок, куб, пирамида и т.п.
2. Если ЗЛП имеет оптимальное решение, то линейная функция принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное (минимальное) значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.
Точка Х называется выпуклой линейной комбинацией точек Х1, Х2,…, Хn, если выполняются условия:
Очевидно, что в частном случае при n = 2 выпуклой линейной комбинацией двух точек является соединяющий их отрезок.
3. Каждому допустимому базисному решению системы ограничений канонической ЗЛП соответствует угловая точка многогранника решений, и наоборот, каждой угловой точке многогранника решений соответствует допустимое базисное решение.
Из двух последних свойств следует: если ЗЛП имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из ее допустимых базисных решений.
Таким образом, экстремум линейной функции ЗЛП надо искать среди конечного числа ее допустимых базисных решений.
Математические модели экономических задач
Определение Математическая модель – это система математических уравнений, неравенств, формул и различных математических выражений, описывающих реальный объект, его составляющие, их характеристики и взаимосвязи между ними.
Определение Экономико-математическая модель представляет собой математическое описание исследуемого экономического процесса или объекта.
Процесс построения экономико-математических моделей включает следующие этапы:
1) выбор переменных;
2) изучение информационной базы;
3) выражение взаимосвязей между переменными, характеризующими объект, в виде уравнений и неравенств;
4) выбор критерия (от гр. kriterion – мерило, оценка, средство для суждения) оптимальности и выражение его в виде математического соотношения.
Решение.Составим экономико-математическую модель задачи.
Реализуем первый этап построения экономико-математической модели и выберем переменные.
Обозначим искомые переменные следующим образом:
Второй этап построения экономико-математической модели включает изучение информационной базы экономического процесса или объекта. Для наглядности процесса моделирования исходную информацию представим в виде таблицы 2.
Таблица 2 – Исходная информация
| Вид сырья | Расход сырья на 1 ед. продукции | Запас сырья |
| П1 | П2 | |
| S1 | ||
| S2 | ||
| Прибыль, ден.ед. |
На третьем этапе построения экономико-математической модели выразим взаимосвязи между переменными, характеризующими объект, в виде уравнений и неравенств.
Для производства всех изделий вида П1 требуется использовать сырье вида S1 в количестве 



Аналогично получим ограничение задачи по сырью вида S2. Неравенство примет вид 
По экономическому смыслу переменных (количество выпускаемой продукции не может быть отрицательным), необходимо выполнение условий 
Тогда ограничений по расходу сырья примет вид
Четвертый этап построения экономико-математической модели заключается в выборе критерия оптимальности и выражение его в виде математического соотношения. В нашей задаче критерием оптимальности является прибыль предприятия от реализации выпускаемой продукции. По условию задачи, прибыль от реализации одной единицы изделия вида П1 составит 2 ден. единиц. Все изделия вида П1 определяют прибыль предприятия в размере 


Итак, экономико-математическая модель данной задачи имеет вид
Эта задача является задачей оптимального использования имеющихся ресурсов. Рассмотрим её формулировку в общем виде.
Задача «об оптимальном использовании ресурсов». Предприятие выпускает n различных изделий: 


Известны технологические коэффициенты 






Дата добавления: 2014-11-24 ; просмотров: 13 | Нарушение авторских прав
Доклад » Математическое моделирование в решении экономических задач» 10кл
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Муниципальное казенное общеобразовательное учреждение
Тулинская средняя общеобразовательная школа
Научно-практическая конференция «Шаг в будущее»
Решение экономических задач
и их применение в жизни
Шульгина Светлана Ивановна
высшей квалификационной категории
Описание механизма решения экономических задач через построение математических моделей.
Экономические задачи, приводящие к исследованию линейной функции.
Математическое программирование как область математики для решения задач на экстремум функции многих переменных
Практические задачи, приводящие к исследованию квадратичной функции.
Слайд №1 П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д. Итак, большую часть своих усилий человек тратит на поиск наилучшего, т.е. оптимального решения поставленной задачи. Как, располагая определенными ресурсами, добиваться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества.
Задачи подобного роста носят общее название – экономические задачи на оптимизацию. В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение второй величины, при котором первая принимает своё наименьшее или наибольшее значение. Математикам удалось разработать методы решения задач на наибольшее и наименьшее значение, или, как их еще называют, задач на оптимизацию. Многие задачи, поиска оптимальных решений, могут быть решены только с использованием методов дифференциального исчисления. Ряд задач такого типа решается с помощью специальных методов линейного программирования, но существуют и такие экстремальные задачи, которые решаются средствами элементарной математики.
Следует различать также два вида задач на оптимизацию. В задачах первого вида улучшение достигается за счет коренных качественных изменений: выбор новых конструктивных решений, переход на новую технологию изготовления. В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели. В данной работе рассмотрены задачи только второго типа. В таких задачах ищутся наибольшее и наименьшее значения функций, зависящих от одной или нескольких переменных.
Цель работы: исследовать способ решения экономических задач с помощью методов математического моделирования.
Гипотеза исследования: я предполагаю, что если выделить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом, можно вывести расчетную формулу, позволяющую. вычислять те или иные параметры, характеризующие явление.
изучить математический аппарат, применяемый при построении математической модели задачи.
Рассмотреть решение экономических задач, приводящие к исследованию линейной функции
решения задач на экстремум функции многих переменных
Прежде чем решать какую – либо жизненную задачу, человек старается взвесить имеющуюся у него информацию, выбрать из нее существенную. И только потом, когда станет более или менее ясно, из чего исходить и на какой результат рассчитывать, он приступает к решению задачи. Иногда описанный процесс называют “уяснением задачи”, фактически же это замена исходной жизненной задачи ее моделью. В осмыслении простейшей жизненной ситуации присутствует модельный подход, хотя человек обычно не замечает своей деятельности по созданию моделей – настолько она для него естественна. Иное дело, если возникающая задача затрагивает ключевые моменты жизни одного человека или какого – либо сообщества людей. Разнообразие информационных аспектов в каждой такой задаче настолько велико, что бывает сложно из всего многообразия информации об изучаемом явлении или объекте выбрать наиболее существенные. В таких случаях необходимо сделать упрощающее предположение, чтобы выделить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом. Все это – предположения, исходные данные, результаты, связи между ними – их называют моделью задачи.
Если построенная модель дает удовлетворительные результаты при решении жизненных задач, то говорят, что модель адекватна рассматриваемому объекту (процессу или явлению). Нередко для решения модельной задачи требуется некоторый инструментарий. Этот инструментарий обычно организуется в виде единого объекта, называемого исполнителем. Чтобы исполнитель мог получить ответ, ему нужны указания, что и как делать. Такие указания часто представляются в виде алгоритма, в котором задаются математические соотношения, связывающие исходные данные и результат. В этом случае говорят о построении математической модели задачи.
Обычно модель возникает как необходимый этап решения конкретной задачи. Однако в дальнейшем может происходить обособление модели от задачи, и модель начинает жить самостоятельно. Примером может служить сюжет движения с постоянной скоростью, который возникал в человеческой деятельности столь часто, что в конце концов обособился от задач и стал составляющей физического знания, называемого “равномерное прямолинейное движение”. Теперь при необходимости решить какую – либо задачу, связанную с равномерным движением пользуются этой готовой моделью процесса. В одних задачах результатом может оказаться время, в других – пройденный путь, в третьих скорость. Остальные параметры модели процесса станут исходными данными.
Если же в задаче фигурирует не равномерное движение, а равноускоренное, то физика и здесь предложит готовую модель в виде формулы:
Соответственно говоря, все естественные науки, использующие математику, можно считать математическими моделями явлений. Например, гидродинамика является моделью движения жидкости, математическая экономика – моделью процессов экономики и т.д. До появления ЭВМ математическое моделирование сводилось к построению аналитической теории явления. Не всегда математическую теорию явления удавалось доводить до возможности вывода формул. Природа оказывалась сложнее возможностей аналитических методов математики. Приходилось вносить значительные упрощения в модель явления, а тем самым обеднять выводы. В этом веке математика пополнилась мощным математическим методом исследования: моделированием сложных систем на ЭВМ. Теперь исследователь ставит перед собой не ту цель, что раньше – вывод расчетной формулы. Теперь он стремится вычислять те или иные параметры, характеризующие явление. Таким путем были исследованы сложные вопросы, связанные с термоядерными реакциями, поведением самолетов в критических ситуациях, влиянием различных факторов на экологические системы, распространением эпидемий и пр.
В настоящее время широко используется математическое моделирование и тогда, когда о физической структуре процесса известно крайне мало. В этом случае строится гипотетическая модель и на ее основе выводятся следствия уже доступные наблюдению. Если такие модели не оправдываются опытом, то они живут недолго и отмирают, уступив место другим моделям, позволяющим познать природу вещей точнее. История науки показывает, сколь большую роль сыграли научные гипотезы и построенные на их основе математические модели явлений.
Математический аппарат, применяемый при построении моделей, весьма разнообразен. Кроме классических разделов математического анализа (дифференциальное и интегральное исчисление) широко используются современные разделы математики, в которых изучаются методы, позволяющие находить оптимальные решения: линейное, нелинейное и динамическое программирование. Для анализа многих операций применяют аппарат теории вероятностей. Это вызвано тем, что исследования проводятся в условиях, определенных не полностью, зависящих от случайных причин. В тех случаях, когда в центре внимания находятся вопросы динамики явлений, широко применяют аппарат дифференциальных уравнений, а в более сложных случаях используется метод статистического моделирования.