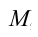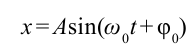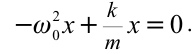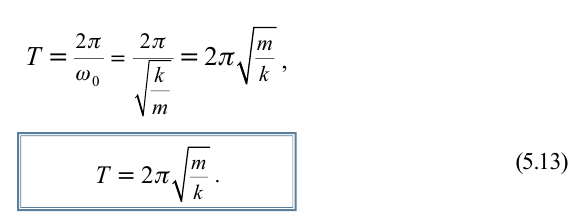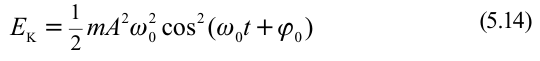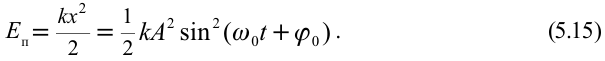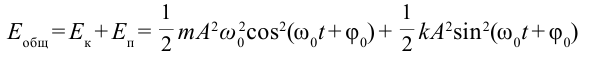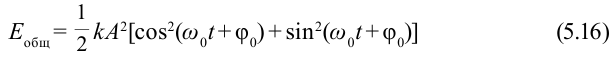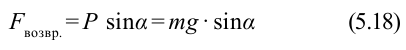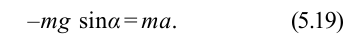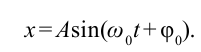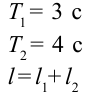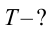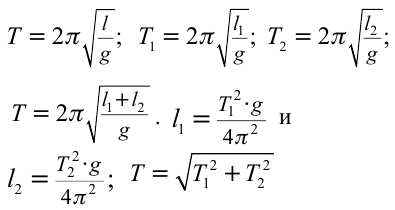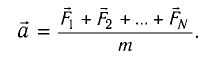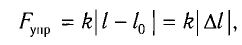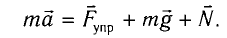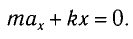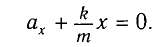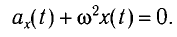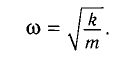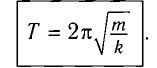Что называется математическим маятником

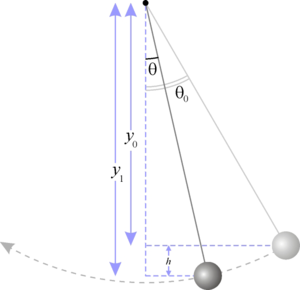
Математический маятник

и не зависит [2] от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

Содержание

Уравнение колебаний маятника

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

где ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах; , где ― длина подвеса, ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

.

Решения уравнения движения

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где — амплитуда колебаний маятника, — начальная фаза колебаний, — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями

Нелинейный маятник

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

где — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.

Параметр определяется выражением

Период колебаний нелинейного маятника

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

, где — период малых колебаний, — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

.

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах 1096-1097 Сентябрьского выпуска заметок американского математического общества 2012 г. [3] :

где — арифметико-геометрическое среднее числел 1 и .

Движение по сепаратрисе

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.

Интересные факты

Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.

Примечания

Ссылки

См. также

Полезное

Смотреть что такое «Математический маятник» в других словарях:

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник … Большой Энциклопедический словарь

МАТЕМАТИЧЕСКИЙ МАЯТНИК — (см. МАЯТНИК). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

математический маятник — Материальная точка, совершающая под действием силы тяжести колебания вдоль заданной плоской кривой. Примечание. Когда эта кривая является окружностью, расположенной в вертикальной плоскости, маятник называется круговым. [Сборник рекомендуемых… … Справочник технического переводчика

математический маятник — см. Маятник. * * * МАТЕМАТИЧЕСКИЙ МАЯТНИК МАТЕМАТИЧЕСКИЙ МАЯТНИК, см. Маятник (см. МАЯТНИК) … Энциклопедический словарь

математический маятник — matematinė švytuoklė statusas T sritis fizika atitikmenys: angl. mathematical pendulum; simple pendulum vok. mathematisches Pendel, n rus. математический маятник, m; простой маятник, m pranc. pendule mathématique, m; pendule simple, m … Fizikos terminų žodynas

Математический маятник — материальная точка, совершающая под действием силы тяжести колебания вдоль дуги окружности, расположенной в вертикальной плоскости. Практически М. м. можно считать груз, подвешенный на нерастяжимой нити, если размеры груза очень малы по… … Большая советская энциклопедия

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник … Большой энциклопедический политехнический словарь

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см Маятник … Естествознание. Энциклопедический словарь

математический маятник — Материальная точка, совершающая под действием силы тяжести колебания вдоль заданной плоской кривой … Политехнический терминологический толковый словарь

Источник

Математический маятник

Содержание:

Определение

Представьте себе некую механическую систему, которая состоит из некой материальной точки (тела), которая висит на нерастяжимой невесомой нити (при этом масса нити ничтожно мала по сравнению с массой тела). Вот такая механическая система и является маятником или осциллятором, как его еще называют. Впрочем, могут быть и другие виды такого устройства. Чем же математический маятник, осциллятор интересен для нас? Дело в том, что с его помощью можно проникнуть в суть многих интересных природных явлений в физике.

Колебания

Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.

Маятниковые часы Гюйгенса.

Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.

Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:

Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).

Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.

Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.

Свойства

У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.

В ходе наблюдений за маятниками были выведены следующие закономерности:

Период

Период маятника – показатель, который представляет период собственно колебаний маятника, их длительность. Формулу периода математического маятника можно записать следующим образом.

Где L – длина нити математического маятника, g – ускорение свободного падения, а π – число Пи, математическая константа.

Период малых колебания математического маятника никак не зависит от массы маятника и амплитуды колебания, в этой ситуации он двигается как математический маятник с заданной длинной.

Практическое применение

Вот мы добрались и до самого интересного, зачем нужен математический маятник и какое его применение на практике в жизни. В первую очередь ускорение математического маятника используется для геологоразведки, с его помощью ищут полезные ископаемые. Как это происходит? Дело в том, что ускорение свободного падения изменяется с географической широтой, так как плотность коры в разных местах нашей планеты далеко не одинакова и там где залегают породы с большей плотностью, ускорение будет немножко больше. А значит, просто подсчитав количество колебаний маятника можно отыскать в недрах Земли руду или каменный уголь, так как они имеют большую плотность, нежели другие рыхлые горные породы.

Также математическим маятником пользовались многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего.

Видео

И в завершение образовательное видео по теме нашей статьи.

Источник

Содержание:

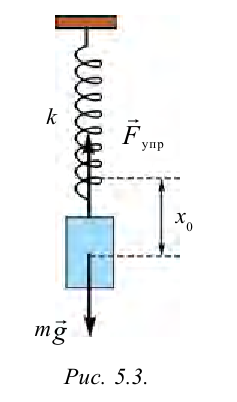
Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 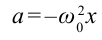, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.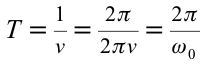

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
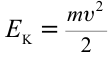
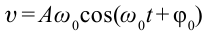
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,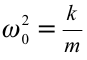

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
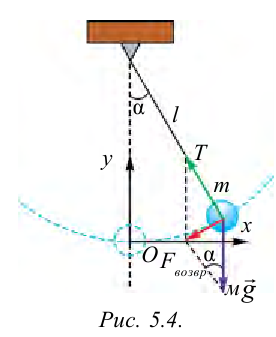
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

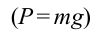
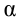
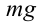
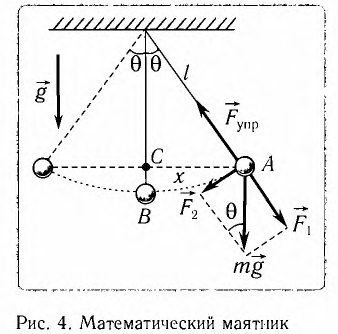
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

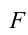
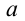
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

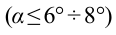
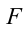
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

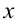
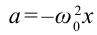
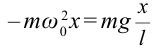
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 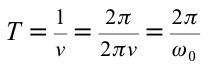получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 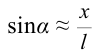и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: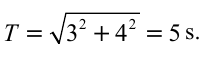

Ответ: 5 cек.

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

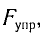
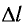
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

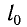
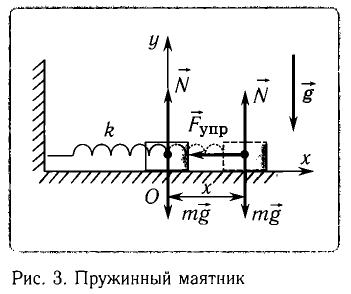
где k — жесткость тела, — длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 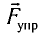направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

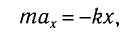
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

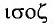
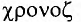
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник